(Beispiel eingefügt.) |
Holzi (Diskussion | Beiträge) |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
== Verwendung == | == Verwendung == | ||
| − | Um die Einwirkung von veränderlichen äußeren Einflüssen auf die Genauigkeit von Messungen zu reduzieren, wird häufig der Mittelwert über die letzten gemessenen Werte gebildet. Es ist | + | Um die Einwirkung von veränderlichen äußeren Einflüssen auf die Genauigkeit von Messungen zu reduzieren, wird häufig der Mittelwert über die letzten gemessenen Werte gebildet. Das gleitende Mittel ist ein einfacher digitaler Tiefpaßfilter und kann so "hochfrequente" Störungen unterdrücken. Besonders gut unterdrückt werden Störfrequenzen, bei denen gerade eine ganze Zahl an Perioden in die Mittelungszeit passen. Es ist unerheblich, woher diese äußeren Einflüsse stammen, sei es z.B. aus Schwankungen der Versorgungsspannung, thermisches Rauschen oder Störungen aus der Umgebung.<br/> Die Bildung eines gleitenden Mittelwertes hat jedoch wenig bis keinen Einfluß auf die Genauigkeit der Ergebnisse, wenn diese durch nahezu konstante äußere Einflüsse (wie z.B. Temperaturdrift eines Verstärkers) verfälscht werden. |
Eine denkbare sinnvolle Anwendung: Ein Roboter ist mit einer größeren Solarzelle ausgerüstet und soll für diese die hellste Stelle in einer halbschattigen Umgebung (im Freien unter Laubbäumen) finden. Jede Positionsänderung kann eine gravierende Änderung der Zellenspannung bewirken. | Eine denkbare sinnvolle Anwendung: Ein Roboter ist mit einer größeren Solarzelle ausgerüstet und soll für diese die hellste Stelle in einer halbschattigen Umgebung (im Freien unter Laubbäumen) finden. Jede Positionsänderung kann eine gravierende Änderung der Zellenspannung bewirken. | ||
| + | |||
| + | == Alternativen zu gleitenden Mittel == | ||
| + | |||
| + | Wenn nicht so viele Ausgabewerte gebraucht werden wie gemessen werden, kann besser eine normale Mittelung durchgeführt werden. Gegebenenfalls kann man dies auch mit einem gleitenden Mittel kombinieren. Für ein einfaches Voltmeter ist es z.B. sinnvoll jeweils 1024 Werte des AD-Wandlers zu mitteln und dann aus je 4 dieser Mittelwerte das gleitende Mittel berechnen. | ||
| + | |||
| + | Relativ einfach und schnell zu berechenen ist auch ein einfacher digitaler Tiefpass erster Ordnung. Vorteilhaft ist dabei, dass man die alten Werte nicht speichern muß, es reicht ein alter Wert. Der Ausgabewert ist dabei einfach das gewichtete Mittel aus dem Ergebnis des letzten Schrittes und dem neuen Messwert. | ||
== Beispiel == | == Beispiel == | ||
| Zeile 15: | Zeile 21: | ||
== C-Code == | == C-Code == | ||
Auf Optimierungen, inline-Funktionen etc. wurde vorerst zugunsten der Lesbarkeit verzichtet. | Auf Optimierungen, inline-Funktionen etc. wurde vorerst zugunsten der Lesbarkeit verzichtet. | ||
| + | Für manche Anwendungen ist es Sinnvoll für den gleitenden Mittelwert einen anderen Datentyp als für die Einzelwerte vorzusehen. Z.B. kann der Mittelwert von ganzen Zahlen durchaus signifikante Nachkommastellen haben. | ||
=== Header === | === Header === | ||
| Zeile 136: | Zeile 143: | ||
return 0; | return 0; | ||
} | } | ||
| − | |||
== Weblinks == | == Weblinks == | ||
| − | + | * [http://de.wikipedia.org/wiki/Gleitender_Mittelwert Wikipedia - Gleitender Mittelwert] | |
[[Kategorie:Quellcode C]] | [[Kategorie:Quellcode C]] | ||
Aktuelle Version vom 30. Dezember 2009, 18:58 Uhr
Der gleitende Mittelwert, auch gleitender Durchschnitt genannt, wird verwendet, um zeitlich aufeinander folgende Reihen von Werten zu glätten; eben den Mittelwert über n aufeinader folgende Werte zu bilden.
| Dieser Artikel ist noch lange nicht vollständig. Der Auto/Initiator hofft das sich weitere User am Ausbau des Artikels beteiligen.
Das Ergänzen ist also ausdrücklich gewünscht! Besonders folgende Dinge würden noch fehlen: viel mehr erklärender Text |
Inhaltsverzeichnis
Verwendung
Um die Einwirkung von veränderlichen äußeren Einflüssen auf die Genauigkeit von Messungen zu reduzieren, wird häufig der Mittelwert über die letzten gemessenen Werte gebildet. Das gleitende Mittel ist ein einfacher digitaler Tiefpaßfilter und kann so "hochfrequente" Störungen unterdrücken. Besonders gut unterdrückt werden Störfrequenzen, bei denen gerade eine ganze Zahl an Perioden in die Mittelungszeit passen. Es ist unerheblich, woher diese äußeren Einflüsse stammen, sei es z.B. aus Schwankungen der Versorgungsspannung, thermisches Rauschen oder Störungen aus der Umgebung.
Die Bildung eines gleitenden Mittelwertes hat jedoch wenig bis keinen Einfluß auf die Genauigkeit der Ergebnisse, wenn diese durch nahezu konstante äußere Einflüsse (wie z.B. Temperaturdrift eines Verstärkers) verfälscht werden.
Eine denkbare sinnvolle Anwendung: Ein Roboter ist mit einer größeren Solarzelle ausgerüstet und soll für diese die hellste Stelle in einer halbschattigen Umgebung (im Freien unter Laubbäumen) finden. Jede Positionsänderung kann eine gravierende Änderung der Zellenspannung bewirken.
Alternativen zu gleitenden Mittel
Wenn nicht so viele Ausgabewerte gebraucht werden wie gemessen werden, kann besser eine normale Mittelung durchgeführt werden. Gegebenenfalls kann man dies auch mit einem gleitenden Mittel kombinieren. Für ein einfaches Voltmeter ist es z.B. sinnvoll jeweils 1024 Werte des AD-Wandlers zu mitteln und dann aus je 4 dieser Mittelwerte das gleitende Mittel berechnen.
Relativ einfach und schnell zu berechenen ist auch ein einfacher digitaler Tiefpass erster Ordnung. Vorteilhaft ist dabei, dass man die alten Werte nicht speichern muß, es reicht ein alter Wert. Der Ausgabewert ist dabei einfach das gewichtete Mittel aus dem Ergebnis des letzten Schrittes und dem neuen Messwert.
Beispiel
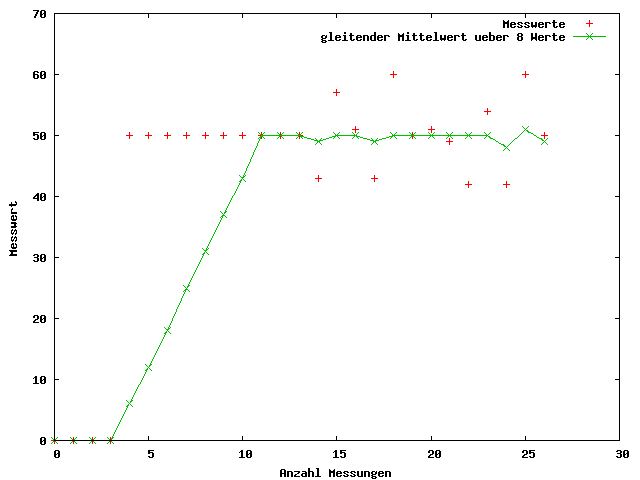
Hier ein Beispiel für die Auswirkungen auf eine Messung. Im Bild werden gestörte Messwerte in rot und die durch den gleitenden Mittelwert geglätteten Werte in grün dargestellt. Ein Nachteil bei der Glättung über viele Werte ist die langsame Reaktion auf Sprünge, wie am Anfang beim Sprung von 0 auf 50 zu sehen ist.
C-Code
Auf Optimierungen, inline-Funktionen etc. wurde vorerst zugunsten der Lesbarkeit verzichtet. Für manche Anwendungen ist es Sinnvoll für den gleitenden Mittelwert einen anderen Datentyp als für die Einzelwerte vorzusehen. Z.B. kann der Mittelwert von ganzen Zahlen durchaus signifikante Nachkommastellen haben.
Header
- FloatingAverage.h
#ifndef FLOATING_AVERAGE_H
#define FLOATING_AVERAGE_H
#include <inttypes.h>
// Ueber wieviele Werte soll der gleitende Mittelwert berechnet werden?
// Zulaessige Werte 1..255
#define SIZE_OF_AVG 8
// Datentyp, ueber den der gleitende Mittelwert berechnet werden soll.
typedef uint16_t tFloatAvgType;
// typedef float tFloatAvgType;
// Wird nur intern fuer die Durchschnittsberechnung benutzt.
// Muss Zahlen fassen koennen, die SIZE_OF_AVG mal groesser als tFloatAvgType sind.
typedef uint32_t tTempSumType;
// typedef float tTempSumType;
// Die Struktur, in der die Daten zwischengespeichert werden
typedef struct
{
tFloatAvgType aData[SIZE_OF_AVG];
uint8_t IndexNextValue;
} tFloatAvgFilter;
// Initialisiert das Filter mit einem Startwert.
void InitFloatAvg(tFloatAvgFilter * io_pFloatAvgFilter,
tFloatAvgType i_DefaultValue);
// Schreibt einen neuen Wert in das Filter.
void AddToFloatAvg(tFloatAvgFilter * io_pFloatAvgFilter,
tFloatAvgType i_ui16NewValue);
// Berechnet den Durchschnitt aus den letzten SIZE_OF_AVG eingetragenen Werten.
tFloatAvgType GetOutputValue(tFloatAvgFilter * io_pFloatAvgFilter);
#endif
Quellcode
- FloatingAverage.c
#include "FloatingAverage.h"
void InitFloatAvg(tFloatAvgFilter * io_pFloatAvgFilter,
tFloatAvgType i_DefaultValue)
{
// Den Buffer mit dem Initialisierungswert fuellen:
for (uint8_t i = 0; i < SIZE_OF_AVG; ++i)
{
io_pFloatAvgFilter->aData[i] = i_DefaultValue;
}
// Der naechste Wert soll an den Anfang des Buffers geschrieben werden:
io_pFloatAvgFilter->IndexNextValue = 0;
}
void AddToFloatAvg(tFloatAvgFilter * io_pFloatAvgFilter,
tFloatAvgType i_NewValue)
{
// Neuen Wert an die dafuer vorgesehene Position im Buffer schreiben.
io_pFloatAvgFilter->aData[io_pFloatAvgFilter->IndexNextValue] =
i_NewValue;
// Der naechste Wert wird dann an die Position dahinter geschrieben.
io_pFloatAvgFilter->IndexNextValue++;
// Wenn man hinten angekommen ist, vorne wieder anfangen.
io_pFloatAvgFilter->IndexNextValue %= SIZE_OF_AVG;
}
tFloatAvgType GetOutputValue(tFloatAvgFilter * io_pFloatAvgFilter)
{
tTempSumType TempSum = 0;
// Durchschnitt berechnen
for (uint8_t i = 0; i < SIZE_OF_AVG; ++i)
{
TempSum += io_pFloatAvgFilter->aData[i];
}
// Der cast is OK, wenn tFloatAvgType und tTempSumType korrekt gewaehlt wurden.
tFloatAvgType o_Result = (tFloatAvgType) (TempSum / SIZE_OF_AVG);
return o_Result;
}
Anwendungsbeispiel
Hier folgt ein Beispiel, das die Anwendung in einem PC-Konsolen-Programm demonstriert
#include <stdio.h>
#include "FloatingAverage.h"
int main(void)
{
// Datenstruktur anlegen:
tFloatAvgFilter FilterVoltageBatt;
// initialisieren und mit 0 fuellen
InitFloatAvg(&FilterVoltageBatt, 0);
AddToFloatAvg(&FilterVoltageBatt, 100);
// jetzt steht 1 mal 100 und 7 mal 0 im Buffer:
printf("100/8 = %d\n", GetOutputValue(&FilterVoltageBatt));
AddToFloatAvg(&FilterVoltageBatt, 200);
// jetzt steht 1 mal 100, 1 mal 200 und 6 mal 0 im Buffer:
printf("300/8 = %d\n", GetOutputValue(&FilterVoltageBatt));
AddToFloatAvg(&FilterVoltageBatt, 300);
AddToFloatAvg(&FilterVoltageBatt, 200);
// jetzt steht 1 mal 100, 2 mal 200, 1 mal 300 und 4 mal 0 im Buffer:
printf("800/8 = %d\n", GetOutputValue(&FilterVoltageBatt));
return 0;
}
Weblinks