E6axis (Diskussion | Beiträge) |
E6axis (Diskussion | Beiträge) |
||
| Zeile 77: | Zeile 77: | ||
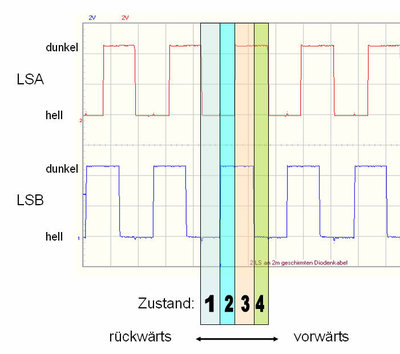
[[Bild:2LSZustand.jpg|400px|thumb|left|2 Lichtschranken (LSA und LSB) liefern phasenversetzte Rechtecksignale. In Vorwärts- und Rückwärtsrichtung ergeben sich unterschiedliche Zustandsfolgen]] | [[Bild:2LSZustand.jpg|400px|thumb|left|2 Lichtschranken (LSA und LSB) liefern phasenversetzte Rechtecksignale. In Vorwärts- und Rückwärtsrichtung ergeben sich unterschiedliche Zustandsfolgen]] | ||
| + | |||
| + | |||
| Zeile 117: | Zeile 119: | ||
<gallery> | <gallery> | ||
Bild:Lochscheibe8.jpg|Lochscheibe 8 | Bild:Lochscheibe8.jpg|Lochscheibe 8 | ||
| − | |||
Bild:Lochscheibe12.jpg|Lochscheibe 12 | Bild:Lochscheibe12.jpg|Lochscheibe 12 | ||
Bild:Lochscheibe15.jpg|Lochscheibe 15 | Bild:Lochscheibe15.jpg|Lochscheibe 15 | ||
| − | |||
Bild:Lochscheibe20.jpg|Lochscheibe 20 | Bild:Lochscheibe20.jpg|Lochscheibe 20 | ||
</gallery> | </gallery> | ||
| Zeile 130: | Zeile 130: | ||
'''f = n * T / 60 s''' | '''f = n * T / 60 s''' | ||
| − | Beispiel: Ein | + | Beispiel: Ein Motor dreht im Leerlauf mit 2370 U/min und hat eine Lochscheibe mit Teilung = 12 an der Motorwelle. Die Frequnz der abzutastenden Signale einer Lichtschranke beträgt 474 Hz. (oben im Osszillogramm dargestellt) |
'''f = 2370 * 12 / 60 s''' | '''f = 2370 * 12 / 60 s''' | ||
| Zeile 136: | Zeile 136: | ||
'''f = 474 Hz''' | '''f = 474 Hz''' | ||
| − | Eine Lichtschranke liefert also ein Rechtecksignal mit f = 474 Hz. Jetzt muss noch das Signal der zweiten Lichtschranke darübergelegt werden. Bei idealen Pegeln sind in einer Periode 4 Schaltzustände abzutasten, also muss die Abtastfrequenz mindestens 4-fach über der Grundfrequenz liegen. Da es in der Praxis aber keine idealen Pegel gibt, muss die Abtastfrequenz noch höher ausgelegt werden. Betrachten wir | + | Eine Lichtschranke liefert also ein Rechtecksignal mit f = 474 Hz. Jetzt muss noch das Signal der zweiten Lichtschranke darübergelegt werden. Bei idealen Pegeln sind in einer Periode 4 Schaltzustände abzutasten, also muss die Abtastfrequenz mindestens 4-fach über der Grundfrequenz liegen. Da es in der Praxis aber keine idealen Pegel gibt, muss die Abtastfrequenz noch höher ausgelegt werden. Betrachten wir noch mal das Osszillogrammm: |
| − | + | ||
| − | + | ||
| − | + | Es fällt auf, das die Zeiten nicht exakt gleich sind, die Zustandszeiten 1 und 3 sind etwas länger als 2 und 4. Das liegt an der Einstellung des Abstandes beider Lichtschranken zueinander, die Phasenlage ist hier nicht genau 90°. Außerdem sind Lochscheibe und Lichtschranken mit kleinen Unregelmäßikeiten, Streuungen, Anstiegs- und Abfallzeiten behaftet, so dass es in einer Periode auch Zeiten gibt, die nicht eindeutig einem der 4 genannten Zustände entsprechen. Für eine sichere Abtastung ist deshalb von der kürzesten (= ungünstigsten) Schaltzeit auszugehen, hier sind es ca. 0,4 Millisekunden, das entspricht 2,5 kHz. Jeder Zustand sollte vom µController schon mindestens 3 bis 4 mal abgetastet werden, so das wir für das Beispiel mindestens ca. 10 kHz Abtastfrequenz einplanen müssen. Die Abtastung soll natürlich sicher sein | |
| Zeile 148: | Zeile 146: | ||
# Sind Lochscheibe und Optik vor Störeinflüssen geschützt? | # Sind Lochscheibe und Optik vor Störeinflüssen geschützt? | ||
# Welche maximale Drehzahl muss noch sicher abgetastet werden? | # Welche maximale Drehzahl muss noch sicher abgetastet werden? | ||
| + | # Phasenlage richtig eingestellt? Optimal sind 90° | ||
|} | |} | ||
Version vom 13. Januar 2011, 19:35 Uhr
Beispiele zum Messen der Drehzahl in Abhängigkeit einer zurückgelegten Strecke oder einer Abgelaufenen Zeit
- Messen der Drehzahl nach jedem Impuls, also in Abhängigkeit einer zurückgelegten Strecke.
- Messen der Drehzahl durch Zählen der Impulse nach Ablauf einer bestimmten Zeit.
- Drehrichtung mit Doppellichtschranke ermitteln
| Dieser Artikel ist noch lange nicht vollständig. Der Auto/Initiator hofft das sich weitere User am Ausbau des Artikels beteiligen.
Das Ergänzen ist also ausdrücklich gewünscht! Besonders folgende Dinge würden noch fehlen: Mehr Grundlagen und vor allem mal praktische Programmbeispiele / Algorithmen etc. |
Inhaltsverzeichnis
Messen der Drehzahl nach jedem Impuls
Dieser Teil beschäftigt sich mit der Optischen Drehzahlmessung mit Hilfe einer Lochscheibe und Gabellichtschranke berechnet über die Periodendauer ohne Drehrichtungserkennung.
Einführung
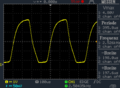
Die Winkelgeschwindigkeit ist die Winkeländerung pro Zeiteinheit. Mit der Lichtschranke und den geometrischen Daten der Lochscheibe kann man nun relativ einfach die Zeit für eine bestimmte Winkeländerung messen. Die Lochscheibe gibt uns die Winkeländerung bei einer Periode vor, bei einer 32er Lochscheibe wären das 11,25° pro Periode , wie in den Bildern vom Oszilloskop zu sehen ändert sich natürlich bei Änderung der Drehzahl die Periodendauer, die Winkeländerung pro Periode ist aber konstant da diese durch die Lochscheibe vor gegeben ist.
Um die Periodendauer zu messen verwende ich den ICP1 (Input Capture Pin) eines Atmega8 der bei steigender Flanke den Timer1 ausliest und in das ICR1 Register schreibt. Läuft der Mikrocontroller auf 8Mhz und wir stellen den Vorteiler des Timers auf 8 so bekommen wir die Periodendauer in µs als Wert.
Auslegen der Lochscheibe
In den meisten fällen definiert der mechanische Aufbau den Durchmesser der Lochscheibe und die Drehzahl die Anzahl der Löcher, der µC muss und die Gabellichtschranke müssen die Impulse auch erfassen können. Wenn man das Drehzahlband abschätzen kann ist es hilfreich sich schon Gedanken um die Programmierung zu machen, denn bei hohen Drehzahlen springt der µC jedes mal in die Interrupt Service Routine rein wenn man es so programmiert wie im Beispiel. Bei hohen Drehzahlen sollte die Auflösung somit gröber sein, bei niedriger feiner.
Berechnungen
Hier folgt nun die Berechnung über die Periodendauer, beachten sollte man das im Bogenmaß gerechnet wird, ein Winkel mit dem Bogenmaß 1 rad hat ein Gradmaß von ca. 57,3°. 11.25° sind also ca. 0,196 rad, das führt später natürlich zu unschönen Rechenoperationen im µC, Stichwort Festkommaarithmetik.
Nach dem umstellen kommt man aber auf eine recht handliche Formel [math]n = \frac{\varphi }{dt \cdot 360}[/math]
Es ist auch eine Überlegung wert ob man die Drehzahl nicht umrechnet sondern mit der Periodendauer arbeitet, das ist zwar nicht so geläufig aber das stört den µC nicht. Mit einem Kalkulationsprogramm hat man sich schnell ein Tool gemacht was die Umrechnung vornimmt.
Messen der Drehzahl durch zählen der Impulse
Dieser Teil beschäftigt sich mit der Optischen Drehzahlmessung mit Hilfe einer Lochscheibe und Gabellichtschranke berechnet über die die Anzahl der Impulse in einer gewissen Zeit.
Einführung
Berechnung
Drehrichtung mit Doppellichtschranke ermitteln
Einführung
Für kontrollierte Bewegungen ist mitunter wichtig, auch die Drehrichtung/Richtungswechsel und Position auszuwerten. Eine Lochscheibe mit einer Gabellichtschranke liefert lediglich Rechteckimpulse, egal wie rum sich die Lochscheibe bewegt. Bringt man eine zweite Gabellichtschranke an der gleichen Lochscheibe leicht versetzt an, bekommt man auch die Drehrichtung mit. Diese Methode ist altbekannt, simpel und leicht nachzubauen. Wenn man die Drehrichtung kennt, ist auch die Position kein Problem mehr. Ausgehend von einer Kalibrierposition können bei Vorwärtsbewegung Inkremente hochgezählt oder bei Rückwärtsbewegung runtergezählt werden.
Interessierte nehmen dazu mal eine PC-Maus mit Kugelantrieb zur Hand. Darin findet man zwei kleine Lochscheiben, die für die X- und Y-Richtung die Impulse erzeugen. Durch spezielle Gabellichtschranken mit 2 phasenversetzten Ausgängen wird auch die Drehrichtung erkannt. Aber es geht natürlich noch einfacher...
Zwei Lichtschranken liefern vier Informationen
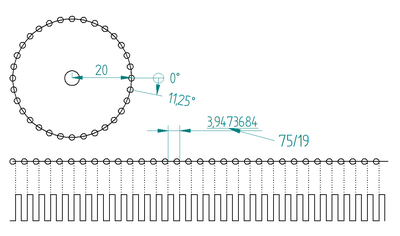
Man nimmt 2 normale Gabellichtschranken und bringt sie so an, das sie im 1,5 fachen Lochabstand die Lochscheibe durchleuchten. Wenn sich Lichtschranke A in der Mitte des Lichtstreifens befindet, ist Lichtschranke B schon an der Grenze zum Schattenstreifen und tritt aus dem Lichtstreifen heraus. Wichtig ist hierbei, das die Lochscheibe in gleich breite Licht- und Schattensegmente eingeteilt ist und die Lichtschranke einen möglichst haarfeinen Lichtstrahl besitzt. (Skizze folgt)
Es ergeben sich nun folgende Kombinationen:
- Zustand 1: LSA = hell und LSB = hell
- Zustand 2: LSA = hell und LSB = dunkel
- Zustand 3: LSA = dunkel und LSB = dunkel
- Zustand 4: LSA = dunkel und LSB = hell
Dreht man die Lochscheibe weiter, wiederholt sich der Vorgang. Die Zustandsfolge ist
1 > 2 > 3 > 4 > 1 > 2 > 3 > 4 > usw.
Bei entgegengesetzter Drehrichtung ändert sich diese Reihenfolge. Betrachtet man wieder vom Zustand 1 ausgehend die Gegenrichtung, ergeben sich nun diese Kombinationen:
- Zustand 1: LSA = hell und LSB = hell
- Zustand 4: LSA = dunkel und LSB = hell
- Zustand 3: LSA = dunkel und LSB = dunkel
- Zustand 2: LSA = hell und LSB = dunkel
Die Zustandsfolge in Gegenrichtung lautet dann: 1 < 4 < 3 < 2 < 1 < 4 < 3 < 2 < usw.
Mit diesem Wissen ist es nun ein Kinderspiel, auch die Änderung der Drehrichtung festzustellen. Dazu muss der letzte Zustand in einer Variable gespeichert und mit dem neu erkannten Zustand verglichen werden. Folgt nach Zustand 1 der Zustand 2, so ist es eine Vorwärtsbewegung. Folgt dem Zustand 1 der Zustand 4, so ist es eine Rückwärtsbewegung. Gleiches Prinzip gilt auch für die restlichen Zustände 2, 3 und 4.
Position, Geschwindigkeit und Beschleunigung
Von jedem der 4 Zustände gibt es also zwei zu unterscheidende Fälle: Vorwärts und Rückwärts. Insgesamt müssen demzufolge 8 Bedingungen zyklisch geprüft und ein Positionszähler entsprechend inkrementiert oder dekrementiert werden und schon hat man eine exakte Streckeninformation. In Worte gefasst ergibt sich folgende Logik:
Ausgangszustand: Beide Lichtschranken sind aus (A=0 UND B=0) und Zustand =1
- WENN (Zustand=1 UND A=0 UND B=1) DANN: Setze Zustand=2, Position inkrementieren, Vor
- WENN (Zustand=1 UND A=1 UND B=0) DANN: Setze Zustand=4, Position dekrementieren, Rück
- WENN (Zustand=2 UND A=1 UND B=1) DANN: Setze Zustand=3, Position inkrementieren, Vor
- WENN (Zustand=2 UND A=0 UND B=0) DANN: Setze Zustand=1, Position dekrementieren, Rück
- WENN (Zustand=3 UND A=1 UND B=0) DANN: Setze Zustand=4, Position inkrementieren, Vor
- WENN (Zustand=3 UND A=0 UND B=1) DANN: Setze Zustand=2, Position dekrementieren, Rück
- WENN (Zustand=4 UND A=0 UND B=0) DANN: Setze Zustand=1, Position inkrementieren, Vor
- WENN (Zustand=4 UND A=1 UND B=1) DANN: Setze Zustand=3, Position dekrementieren, Rück
Diese Prüfung muss während der Bewegung ständig wiederholt werden, damit alle Pegelwechsel der beiden Lichtschranken erfasst werden. Nur so ist es möglich, die exakte Position zu verfolgen. Dafür bieten sich 2 Möglichkeiten: Entweder die Prüfung wird im Hauptprogramm ständig durchlaufen (Polling) oder ein Timer-Interrupt ruft regelmäßig die Prüfung auf. Hier soll nur die zweite, also Interruptvariante betrachtet werden, weil sie mehr Vorteile bringt. Weiter unten im Artikel ist dazu ein Beispiel in Sprache C zu finden.
Zuvor muss aber eine sinnvolle Auslegung von Lochscheibe, Drehzahl und Positionsbereich gefunden und in Einklang mit den Resourcen des verwendeten µControlles gebracht werden. Dazu folgende Betrachtungen:
Wenn 2 phasenversetzte Lichtschranken je Hell-/ Dunkelzyklus bereits 4 Positionen liefern, benötigt die Lochscheibe nur halb so viel "Löcher" wie eine Lochscheibe mit nur einer Lichtschranke. Eine 15er Lochscheibe liefert demzufolge 15x4 = 60 Positionen auf 360°, das sind 6° je erfasster Position. Entscheidend ist, an welchem Antriebsteil die Lochscheibe montiert ist und mit welcher Untersetzung zwischen Motor und Abtriebswelle(Rad) gearbeitet wird. Ist die Lochscheibe an der Motorwelle angebracht, würde bei einer angenommenen Untersetzung von 10:1 eine erfasste Position nur 0,6° an der Abtriebswelle ausmachen.
Man muss sich klar machen, welche Positioniergenauigkeit nötig ist. Dabei gilt: Auslegung so genau wie nötig, nicht wie möglich. Weiter muss geklärt werden, wo man die Lochscheibe sinnvoll anbringt. Sie darf im Betrieb weder verschmutzt oder beschädigt werden. Fahrmodelle ziehen Staub, Haare etc. gern an, gut beraten ist man mit einer verkapselten Optomechanik. Ein weiterer Faktor ist die Drehzahl (Leerlauf und Vollast) des Motors, weil diese die Frequenz der abzutastenden Signale beeinflusst. Zwischen Drehzahl n [U/min], Frequenz f [Hz] und Teilung T besteht folgender Zusammenhang:
f = n * T / 60 s
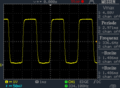
Beispiel: Ein Motor dreht im Leerlauf mit 2370 U/min und hat eine Lochscheibe mit Teilung = 12 an der Motorwelle. Die Frequnz der abzutastenden Signale einer Lichtschranke beträgt 474 Hz. (oben im Osszillogramm dargestellt)
f = 2370 * 12 / 60 s
f = 474 Hz
Eine Lichtschranke liefert also ein Rechtecksignal mit f = 474 Hz. Jetzt muss noch das Signal der zweiten Lichtschranke darübergelegt werden. Bei idealen Pegeln sind in einer Periode 4 Schaltzustände abzutasten, also muss die Abtastfrequenz mindestens 4-fach über der Grundfrequenz liegen. Da es in der Praxis aber keine idealen Pegel gibt, muss die Abtastfrequenz noch höher ausgelegt werden. Betrachten wir noch mal das Osszillogrammm:
Es fällt auf, das die Zeiten nicht exakt gleich sind, die Zustandszeiten 1 und 3 sind etwas länger als 2 und 4. Das liegt an der Einstellung des Abstandes beider Lichtschranken zueinander, die Phasenlage ist hier nicht genau 90°. Außerdem sind Lochscheibe und Lichtschranken mit kleinen Unregelmäßikeiten, Streuungen, Anstiegs- und Abfallzeiten behaftet, so dass es in einer Periode auch Zeiten gibt, die nicht eindeutig einem der 4 genannten Zustände entsprechen. Für eine sichere Abtastung ist deshalb von der kürzesten (= ungünstigsten) Schaltzeit auszugehen, hier sind es ca. 0,4 Millisekunden, das entspricht 2,5 kHz. Jeder Zustand sollte vom µController schon mindestens 3 bis 4 mal abgetastet werden, so das wir für das Beispiel mindestens ca. 10 kHz Abtastfrequenz einplanen müssen. Die Abtastung soll natürlich sicher sein
|
Baustelle
weiterführende Informationen: Inkrementalgeber
Vor und Nachteile der Messmethoden