K |
|||
| Zeile 110: | Zeile 110: | ||
Verändert man die "Wirksame Oberfläche" A, so verändert sich proportional dazu die Kapazität C. | Verändert man die "Wirksame Oberfläche" A, so verändert sich proportional dazu die Kapazität C. | ||
| + | |||
| + | |||
== Bauformen == | == Bauformen == | ||
| − | + | ||
| − | Die heutzutage verfügbaren Bauformen spiegeln den Fortschritt in der Entwicklung sowie den immer weiter steigenden Preisdruck in der Fertigung wieder. Auf die ursprünglich vorhandene mechanischen Befestigung mittels Schrauben folgte die Entwicklung mit Anschlussdrähten für die Leiterplattenmontage (liegende Bauform = axial; stehende Bauform = radial). Heute sind, verbunden mit der Bauteilminiaturisierung, zudem noch die oberflächenmontierbaren SMD-Bauelemente in allen möglichen Varianten verfügbar. | + | Die heutzutage verfügbaren Bauformen spiegeln den Fortschritt in der Entwicklung sowie den immer weiter steigenden Preisdruck in der Fertigung wieder. Auf die ursprünglich vorhandene mechanischen Befestigung mittels Schrauben folgte die Entwicklung mit Anschlussdrähten für die Leiterplattenmontage (liegende Bauform = axial; stehende Bauform = radial). Heute sind, verbunden mit der Bauteilminiaturisierung, zudem [[Bild:Kondensator-Bauformen.jpg|thumb|Verschide Bauformen von Kondensatoren]]noch die oberflächenmontierbaren SMD-Bauelemente in allen möglichen Varianten verfügbar. |
| + | |||
Daneben finden sich aber auch immer noch Bauformen für speziellen Anforderungen, z.B. Flachband- oder Schraubanschlüsse für Hochstromanwendungen oder Durchführungskondensatoren im HF-/UHF-Bereich. | Daneben finden sich aber auch immer noch Bauformen für speziellen Anforderungen, z.B. Flachband- oder Schraubanschlüsse für Hochstromanwendungen oder Durchführungskondensatoren im HF-/UHF-Bereich. | ||
Version vom 31. Mai 2011, 13:07 Uhr
Ein Kondensator ist ein passives Bauelement mit der Eigenschaft, elektrische Ladung und somit Energie zu speichern. Er besteht aus zwei elektrisch leitenden Flächen (Elektroden). Zwischen diesen befindet sich immer das Dielektrikum, ein Bereich mit isolierenden Eigenschaften (im einfachsten Fall Luft). Die einfachste Bauform eines Kondensators besteht also aus zwei parallelen Platten mit elektrischen Anschlüssen.
Inhaltsverzeichnis
Grundlagen
Wird eine Spannung an die Anschlüsse eines ungeladenen Kondensators angelegt, so fließt zeitabhängig ein elektrischer Strom, welcher eine Elektrode positiv und die andere negativ auflädt. Diese elektrische Ladung des Kondensators bleibt erhalten, wenn er von der Spannungsquelle getrennt wird: Der Kondensator hält seine Spannung. Entnimmt man dem Kondensator Ladung (also Strom), so sinkt seine Spannung wieder.
Die gespeicherte Ladung ist proportional zur Spannung zwischen den Elektroden des Kondensators. Diese Proportionalität wird als Kapazität bezeichnet, sie ist das wesentliche Merkmal eines Kondensators.
Ein weiteres wichtiges Merkmal ist die Maximalspannung, die ein Kondensator zwischen seinen Elektroden ertragen kann. Wird diese Spannung überschritten, ist das Dielektrikum nicht mehr in der Lage, seine isolierenden Eigenschaften zu behalten. Es kommt zu einem Durchschlagen der Ladungsträger, der Kondensator wird zerstört.
Kondensator an Gleichspannung
In dem Moment, in dem man eine Spannungsquelle mit einem ungeladenen Kondensator verbindet, wird die mit dem Pluspol verbundene Platte positiv, die mit dem Minuspol verbundene Platte negativ aufgeladen. Dabei fließt ein von der Kapazität des Kondensators abhängiger Ladestrom. Nach diesem Ladevorgang findet unter der Voraussetzung einer gleichbleibenden Spannung kein weiterer Stromfluss statt. Misst man dann mit einem Spannungsmessgerät die Spannung zwischen den beiden Platten, stimmt diese exakt mit der angelegten Spannung überein.
Klemmt man dann den Kondensator von der Spannungsquelle ab, bleibt die vorhandene Ladung erhalten.
Schließt man jetzt einen Verbraucher an den Kondensator an, fließt die Ladung über diesen Verbraucher ab; der Kondensator wird entladen.
Ein Kondensator sperrt also Gleichspannung, speichert aber die Ladung. Das Fließen eines Stromes zum Schaltzeitpunkt ist hierbei kein Widerspruch, denn das Schalten ist eine Veränderung der Spannung und damit keine Gleichspannung. Wenn nach ganz kurzer Zeit der stationäre Zustand erreicht ist, fließt kein Strom mehr; denn Strom kann nur fließen, wenn sich die Spannung am Kondensator ändert.
Kondensator an sinusförmiger Spannung
Aus den mathematischen Grundlagen folgt, dass bei einer sinusförmigen Spannung der Strom einen cosinusförmigen Verlauf mit der gleichen Frequenz wie die Spannung besitzt. Der Strom ist durch die Cosinus-Funktion um 90° phasenverschoben, d.h. er eilt der Spannung mit einer Phasenverschiebung von 1/4 Periode voraus (eine Spannung kann am Kondensator also nur anliegen, wenn vorher Strom in ihn geflossen ist).
Wenn man bei konstanter Spannung die Frequenz erhöht, nimmt die Änderungsgeschwindigkeit der Spannung zu. Damit muss in kürzerer Zeit die gleiche Ladung bewegt werden, folglich muss die Amplitude des Stroms zunehmen. Der Strom ist dabei proportional zur Frequenz, bei doppelter Frequenz fließt daher auch der doppelte Strom.
Technisch bedeutsame Größen
Hier sollen nur die für einen Hobby-Bastler technisch interessanten Kenngrößen aufgeführt werden.
- Kapazität
Die Kapazität (C) eine Kondensators gibt an, wieviel Ladung (Q) pro Spannung (U) gespeichert werden kann: C = Q / U. Die Einheit für Kapazitäten ist Farad: 1 F = 1 As/V.
Werden mehrere Kondensatoren parallel zueinander geschaltet, so addieren sich ihre Kapazitäten (wie bei der Reihenschaltung von Widerständen). Bei einer Reihenschaltung von Kondensatoren wird die Summe ihrer Reziprokwerte addiert (wie bei der Parallelschaltung von Widerständen).
- Spannungsfestigkeit
Die Isolierschicht eines Kondensators kann nur eine bestimmte Spannung aushalten. Wenn diese Spannung überschritten wird, wird in der Regel der Kondensator zerstört. Einige Folienkondensatoren sind selbstheilend und können kurze Überspannungen vertragen, verlieren dabei aber an Kapazität. Die angebenene Spannung ist immer der garantierte Mindestwert, die ein Kondensator ohne Beschädigung aushält.
- Tangens Delta
Bei einem realen Kondensator ist die Phasenverschiebung (Sinus) zwischen Strom und Spannung nicht wie ideal gefordert 90 Grad, sondern um den Werte "Delta" kleiner. Der Hauptgrund für die Abweichungen sind Verluste im Dielektrikum. Der Ausdruck "Tangens Delta" gibt gerade das Verhältnis von Verlustleistung zu Scheinleistung and.
- Strombelastbarkeit
Der reale Kondensator hat einen internen Serienwiderstand und zusätzlich Verluste im Dielektrikum. Wegen der damit verbundenen Erwärmung darf nur ein begrenzter (Wechsel-)Strom durch den Kondensator fließen. Die Strombelastbarkeit ist bei Elkos und einigen Folienkondensatoren relativ niedrig. Wichtig ist diese Beschränkung in Schaltnetzteilen.
- Selbstentladung
Ein aufgeladener realer Kondensator entlädt sich mit der Zeit von selbst. Dieser Effekt kann durch einen endlichen Isolationswiderstand Ris des Dielektrikums beschrieben werden, der zu einem idealen Kondensator C parallel geschaltet ist. Der dabei fließende Strom wird als Leckstrom bezeichnet.
Die Selbstentladezeitkonstante [math]\tau[/math] = Ris * C ist zudem ein Maß für die Güte der Isolation eines Kondensators.
Neuere Papier- und Kunststofffolienkondensatoren haben einen Isolationswiderstand zwischen 6 und 12 GΩ, daraus ergibt sich eine Selbstentladezeit (nach 5[math]\tau[/math] gilt ein Kondensator als entladen) zwischen 10.000 und 20.000 s (etwa 3 bis 6 Stunden). Für Elektrolytkondensatoren ist der Isolationswiderstand und damit auch die Selbstentladezeit deutlich niedriger.
Diese Zeitkonstante ist wichtig, wenn ein Kondensator zur Speicherung eines Spannungswertes eingesetzt werden soll.
Praktische Bedeutung
Ein Kondensator setzt durch seine Konstruktion einem Gleichstrom einen im Idealfall unendlich hohen Widerstand entgegen. Je höher aber die Frequenz eines angelegten Wechselstromes wird, desto niedriger wird der frequenzabhängige Blindwiderstand des Kondensators; für (theoretisch) unendlich hohe Frequenzen ist dieser Blindwiderstand gleich Null. Diese Eigenschaft macht den Kondensator zu einem Hochpass - hohe Frequenzen können nahezu ungehindert passieren, niedrige Frequenzen werden mehr oder weniger stark gedämpft. Weitere Informationen findet man unter Filter (Elektronik).
Bauarten
Keramik-Kondensator (Kerko)
Wie der Name schon sagt, besteht bei diesen Kondensatoren das Dielektrikum aus einem keramischen Material. Verwendet werden z. B. Titandioxid oder Bariumtitanat, beigemischt werden u.a. Aluminium-Silikate, Magnesium-Silikate oder Aluminiumoxide.
Keramik-Kondensatoren bilden eine große Gruppe von Kondensatoren im Kapazitätsbereich von 0,5 pF bis zu einigen 100 µF. Von der verwendeten Keramikart sind im wesentlichen 2 Klassen zu unterscheiden:
Klasse 1: Normale Keramiken (z.B. NP0) erlauben geringe Verluste und Temperaturkoeffizienten, allerdings nur relativ geringe Kapatzitäten (normal bis ca. 1 nF). Diese Kondensatoren eignen sich gut für Hochfrequenz- und Filteranwendungen.
Klasse 2: Ferroelektrische Keramiken geben hohe Kapazitäten, aber auch eine starke Nichtlinearität und Temperaturabhängigkeit. Auch reagieren diese Kondesatoren auf mechanische Spannung und können so Störungen einfangen. Diese Kondensatoren sind im wesenlichen als Entstörkondensator, Energiespeicher oder Abblockkondensator geeignet.
Folien-Kondensator
Hierbei werden Folien aus Kunststoff als Dielektrikum verwendet. Sie werden in zwei Ausführungen hergestellt:
Kunststoff-Folienkondensatoren mit Metallbelag bestehen aus je zwei Lagen Metallfolie und Kunststofffolie. Diese sind abwechselnd geschichtet und üblicherweise aufgewickelt.
Ein metallisierter Kunststoff-Folienkondensator besteht aus zwei Kunststofffolien, die auf beiden Seiten mit Aluminium bedampft sind und aufgewickelt oder geschichtet werden. Diese Kondensatorart ist bei einem Durchschlag selbstheilend, da die dünne Metallschicht vom Lichtbogen um den Durchschlagkanal herum verdampft wird.
Folienkondensatoren sind vielseitig verwendbar, hauptsächlich in Filtern, Taktgeben und bei Hochspannung. Der gängige Kapazitätsbereich reicht von etwa 10 pF bis 100µF. Wegen der geringen Temperaturbeständigkeit gibt es nur wenige Folienkondensatoren als SMD Bauform.
Elektrolyt-Kondensator (Elko)
Die große Gruppe der Elektrolyt-Kondensatoren gibt es in verschiedenen Technologien: Als Aluminium-Elko mit Aluminiumoxid, als Tantal-Elko mit Tantal-Pentoxid oder als Niob-Elko mit Niob-Pentoxid als Dielektrikum.
Bei diesen Kondensatoren wird auf dem Metall der Anode durch Elektrolyse eine nichtleitende Isolierschicht als Dielektrikum erzeugt. Der Elektrolyt (fest, flüssig oder eine Paste) bildet dabei die Kathode (Gegenelektrode). Die Stromzuführung zum Elektrolyten erfolgt über Folien gleichen Metalls wie das der Anode oder über eine geeignete Kontaktierung des Elektrolyten.
Die Anode eines Elektrolyt-Kondensators wird zur Vergrößerung der Oberfläche auf verschiedene Arten strukturiert. Auf Grund der großen Oberfläche und des äußerst dünnem Dielektrikums können mit Elektrolyt-Kondensatoren bei kleiner Bauweise relativ hohe elektrische Kapazitäten von bis zu einem Farad erreicht werden.
Elektrolyt-Kondensatoren sind fast immer gepolte Bauelemente. Elkos dürfen nicht mit falscher gepolter Spannung betrieben werden und können schon bei geringer Überspannung zerstört werden (in beiden Fällen besteht Explosionsgefahr bei Aluminium Elkos). Der Ausfall von Tantal-Elkos (passiert relativ leicht) führt in der Regel zu einem Kurzschluß.
Niob-Elektrolytkondensatoren ähneln Tantal-Elektrolytkondensatoren; sie stellen bei Spannungen zwischen 1,8 V und 6 V eine kostengünstige Alternative dar.
Elektrolyt-Kondensatoren können nur eingesetzt werden, wenn ein Verpolungsschutz sichergestellt ist. Auf Grund ihrer hohen Kapazität geschieht dies meist im Bereich der Spannungsversorgung und -stabilisierung.
Durch die relativ hohen Verluste (ESR) können größere Ströme Elkos erwärmen und auf Dauer auch zerstören (nicht selten Ursache für defekte Motherboards). Besonders in Schaltnetzteilen muß darum auf die Strombelastbarkeit der Elkos geachtet werden.
Doppelschicht-Kondensator
Auch Superkondensatoren genannt; Markennamen Gold Cap, Supercap, UltraCap, BoostCap u.a.
Sie zeichnen sich durch die höchste Energiedichte bei Kondensatoren aus. Ihre hohe Kapazität basiert auf einem flüssigen Elektrolyten, der an der Grenzschicht zu den Elektroden ein dünnes Dielektrikum von wenigen Atomlagen bilden. Dies wird kombiniert mit einer meist aus Aktivkohle hergestellen großen Elektrodenoberfläche.
Doppelschicht-Kondensatoren haben nur eine Spannungsfestigkeit von ca. 5,5 Volt, eine begrenzte Anzahl von Lade-Entladezyklen (typischerweise eine Million) und eine geringe Lebensauer bei erhöhter Umgebungstemperatur (nur ca. tausend Stunden bei 70 °C). Doppelschicht-Kondensatoren sind wie Elektrolytkondensatoren ebenfalls gepolte Bauelemente.
Da Doppelschicht-Kondensatoren im Gegensatz zu Akkus nicht überladen werden können, werden sie ohne zusätzlich notwendige Schaltungen meist als geräteinterne unterbrechungsfreie Spannungsversorgung eingesetzt.
Sonderarten
Metallpapier-Kondensator (MP)
Sie bestehen aus je zwei Lagen ölgetränktem Papier (als Dielektrikum) und Metallfolie, die aufgewickelt sind. Das Papier dient als mechanische Trennung der Elektroden, das Öl bestimmt die dielektrischen Eigenschaften. MP-Kondensatoren finden vor allem im Bereich der Leistungselektronik, z.B. bei Wechselstrommotoren, Verwendung; im Hochspannungsbereich sind sie selbstheilend.
Glimmer-Kondensator
Hierbei wird ein Dielektrikum aus dem natürlich vorkommenden Mineral Glimmer verwendet, welches eine hohe Spannungsfestigkeit aufweist und auf Grund seiner Struktur in dünne Blättchen spaltbar ist (bis zu 20 µm). Kondensatoren aus diesem Material werden aufgrund der niedrigen Verlustfaktoren in der Sendetechnik und aufgrund ihre Konstanz in Schwingkreisanwendungen für hohe Anforderungen verwendet.
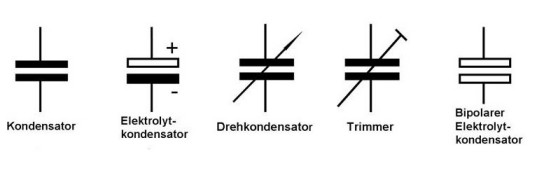
Trimm- und Drehkondensator
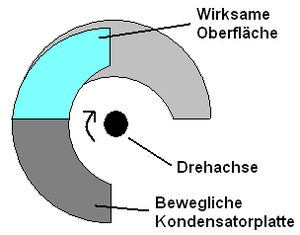
Trimm- bzw. Drehkondensatoren sind Kondensatoren, welche in der Kapazität variabel sind. Durch das verdrehen von mindestens zwei Kondensatorplatten ineinander, kann die Kapazität erhöht oder verringert werden. Da diese Kondensatoren meist nur Luft als Dielektrikum verwenden, ist die Kapazität sehr gering (etwa 1-100pF). Die Kondensatoren können zum Beispiel zum Abstimmen von Radioempfängern und Sendern sowie zum genauen Abgleich von Schwingquarzen verwendet werden.
Die Kapazität ergibt sich aus der Gleichung für Plattenkondensatoren: C = Epsilon_0 * Epsilon_r * A / d
Verändert man die "Wirksame Oberfläche" A, so verändert sich proportional dazu die Kapazität C.
Bauformen
Die heutzutage verfügbaren Bauformen spiegeln den Fortschritt in der Entwicklung sowie den immer weiter steigenden Preisdruck in der Fertigung wieder. Auf die ursprünglich vorhandene mechanischen Befestigung mittels Schrauben folgte die Entwicklung mit Anschlussdrähten für die Leiterplattenmontage (liegende Bauform = axial; stehende Bauform = radial). Heute sind, verbunden mit der Bauteilminiaturisierung, zudem noch die oberflächenmontierbaren SMD-Bauelemente in allen möglichen Varianten verfügbar.
Daneben finden sich aber auch immer noch Bauformen für speziellen Anforderungen, z.B. Flachband- oder Schraubanschlüsse für Hochstromanwendungen oder Durchführungskondensatoren im HF-/UHF-Bereich.
Anwendungsbeispiele
Filter
Die einfachste Verwendungsmöglichkeit von Kondensatoren findet man im Bereich der Frequenzfilter. Dort werden sie, zusammen mit Widerständen und ggf. auch Spulen als RC- oder RLC-Glieder ausgelegt. In ihrer Funktionalität unterscheidet man die so entstehenden Schaltungen zwischen Tief-, Hoch- oder Bandpassfiltern.
Ausführliche Informationen dazu siehe unter Filter (Elektronik)
Schwingkreis
Ein Schwingkreis ist eine Reihen- oder Parallelschaltung aus Kondensator und Spule. Sie ist so aufgebaut, daß die vorhandene Energie zwischen dem elektischen Feld des Kondensators und dem magnetischen Feld der Spule periodisch ausgetauscht wird.
Ein Schwingkreis schwingt theoretisch unendlich lange mit seiner idealen Resonanzfrequenz. Infolge der realen Bauteile und deren ohmschen Anteilen gilt jedoch eine davon abweichende reale Resonanzfrequenz; zudem nimmt die Amplitude der Schwingung im Laufe der Zeit ab, man spicht von einer „gedämpften Schwingung“. Durch aktive Verstärkerschaltungen muß regelmäßig wieder Energie zugeführt wird. Eine solche Schaltung bildet dann einen Oszillator.
Aus einzelnen Bauteilen diskret aufgebaute Schwingkreise werden heute hauptsächlich in der HF-Technik als Abstimmkreise, Oberwellen- oder Frequenzfilter eingesetzt. Hier kommen dann auch oft in ihren Kenngrößen veränderliche Bauteile (Trimmkondensatoren, Kapazitätsdioden, Spulen mit variablen Kernen) zum Einsatz.
In der Digitaltechnik haben diskret aufgebaute Schwingkreise wegen des hohen Schaltungsaufwandes so gut wie keine Bedeutung. Hier werden Schwingquarze oder Quarzoszillatoren wegen des einfacheren Schaltungsaufwandes sowie ihrer höheren Frequenzgenauigkeit bevorzugt.
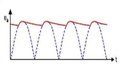
Spannungsstabilisierung
Die hohe Welligkeit einer gleichgerichteten Wechselspannung erzwingt eine Glättung vor der Spannungsstabilisierung. Nur so können die Spannungsregler ihre Arbeit einwandfrei erledigen und eine saubere Betriebsspannung zur Verfügung stellen. Bild a. zeigt den Verlauf der Spannung vor und nach einer Gleichtichtung. In Bild b. ist der Einsatz eines Elektrolytkondensators direkt am Ausgang der Gleichrichterschaltung zu sehen. Bild c. zeigt den Spannungsverlauf Ub auf der Ausgangsseite dieses Kondensators (entspricht der Eingangsspannung des Spannungsreglers). Bei der Auswahl des Kondensators muß auf die Spannungsfestigkeit, Kapazität und Strombelastbarkeit geachtet werden.
Signalentstörung
Die häufigste Anwendung eines Kondensators im Bereich der Signalentstörung ist seine Verwendung als Abblockkondensator
(Kommentar: Auch wenn Gelehrte streiten mögen, ob das nicht eher zur Spannungsstabilisierung dient... aber die Spannung ist ja stabil im Bereich dessen, was digitale ICs vertragen (müssten)!).
Anmerkungen
Der Autor möchte hier weder die an anderen Stellen zu findenden Formelsammlungen wiedergeben, noch mit diesem Artikel ein Fachbuch ersetzten. Einzig die Grundlagen, die (aus eigener Erfahrung) für einen Hobby-Bastler von Interesse sind, sollen hier dargestellt werden.
| Dieser Artikel ist noch lange nicht vollständig. Der Auto/Initiator hofft das sich weitere User am Ausbau des Artikels beteiligen.
Das Ergänzen ist also ausdrücklich gewünscht! Besonders folgende Dinge würden noch fehlen: Ausbau der einzelnen Kapitel - Bilder einfügen! |
Weblinks
Autor
--Williwilli 08:59, 25. Jul 2008 (CEST)