Waste (Diskussion | Beiträge) K (→Dimensionierung mit dem Bodediagramm) |
Waste (Diskussion | Beiträge) K (→PID-Regler) |
||
| Zeile 182: | Zeile 182: | ||
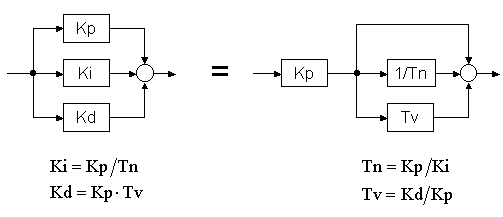
'''Alternative PID-Reglerstruktur:''' | '''Alternative PID-Reglerstruktur:''' | ||
| − | Es gibt 2 Darstellungsmöglichkeiten, die inhaltlich identisch sind. | + | Es gibt 2 Darstellungsmöglichkeiten, die inhaltlich identisch sind. In der analogen Regeltechnik ist noch die Darstellung mit der Nachstellzeit '''Tn''' und der Vorhaltezeit '''Tv''' üblich. Die Umrechnung zwischen den beiden Strukturen ist mit den angegebenen Formeln möglich. |
[[Bild:PIDstruktur.gif]] | [[Bild:PIDstruktur.gif]] | ||
Version vom 29. Dezember 2005, 12:24 Uhr
Inhaltsverzeichnis
Einleitung
Regelungen sind ein Bestandteil unseres Lebens und das nicht nur seit Erfindung der Dampfmaschine. Allein schon der aufrechte Gang funktioniert nur mit Regelung. Dabei wirken die Sinne als Sensoren, das Gehirn als Regler und die Muskeln als Aktuatoren. Weitere Regelungen in unserem Körper sind z.B. die Konstanthaltung der Körpertemperatur, der Blutdruck, die Anpassung der Pupille auf Helligkeitsänderungen usw. Im technischen Zeitalter ist der erste geschichtlich bedeutende Regler der Fliehkraftregler von James Watt, der für die Drehzahlregelung seiner Dampfmaschine eingesetzt wurde. Seitdem ist die Regelungstechnik aus keinem Technikbereich mehr wegzudenken. Die Regelungstechnik begegnet uns im täglichen Leben auf Schritt und Tritt: Der Temperaturregler der Zentralheizung, der Temperaturregler des Kühlschranks, der Regler für die Belichtungsautomatik im Fotoapparat, das ABS-System im Auto und die Netzspannungs- und Frequenzregelung des europäischen Versorgungsnetzes sind nur einige wenige Beispiele aus diesem Bereich.
Der Begriff Regelung ist zu unterscheiden von dem im allgemeinen Sprachgebrauch oft synonym gebrauchten Begriff der Steuerung. Das Steuern ist ein rein vorwärts gerichteter Prozess ohne Rückkopplung. Die Ausgangsgröße wird dabei nicht überwacht und kann sich durch Störungen von außen verändern. Ein Beispiel ist die Steuerung eines Motors mit einer einstellbaren Spannung. Durch Laständerungen wird sich die Drehzahl des Motors ändern. Soll nun die Drehzahl konstant gehalten werden, bedarf es einer Rückkopplung um über die Spannung die Drehzahl anzupassen. Diese Rückkopplung ist das Kennzeichen einer Regelung. Das Regeln ist ein Vorgang, bei dem die Ausgangsgröße, im Beispiel die Drehzahl, fortlaufend überwacht wird und bei Abweichung über die Stellgröße, im Beispiel die Spannung, korrigiert wird. Der sich dabei ergebende Wirkungsablauf findet in einem geschlossenen Kreis, dem Regelkreis, statt.
Autor Waste
Der Regelkreis
Das Prinzip einer Regelung ist das fortlaufende: Messen - Vergleichen - Stellen
http://www.roboternetz.de/wiki/uploads/Main/Regelkreis1.gif
| Messen: | Die Regelgröße wird direkt oder mittels Sensoren gemessen. |
| Vergleichen: | Der Wert der Regelgröße wird mit dem Sollwert verglichen. Die Differenz ist die Regelabweichung. |
| Stellen: | Aus der Regelabweichung wird unter Berücksichtigung der dynamischen Eigenschaften der Regelstrecke die Stellgröße bestimmt. |
Ein Regelkreis dient dazu, eine vorgegebene physikalische Größe (Regelgröße) auf einen gewünschten Wert (Sollwert) zu bringen und dort zu halten, unabhängig von eventuell auftretenden Störungen.
Um die Regelungsaufgabe zu erfüllen, muss der Augenblickswert der Regelgröße - der Istwert - gemessen und mit dem Sollwert verglichen werden. Bei auftretenden Abweichungen muss in geeigneter Art und Weise nachgestellt werden.
http://www.roboternetz.de/wiki/uploads/Main/Regelkreis2.gif
Ein typisches Beispiel für einen Regelkreis - eine Geschwindigkeitsregelung - wird im nächsten Bild gezeigt. Die Sollgeschwindigkeit ist 80 km/h. Durch eine äußere Störung, in dem Fall eine Steigung, verlangsamt sich das Fahrzeug auf 70 km/h. Die Abweichung wird durch das Tachometer erfasst und als Korrekturmaßnahme wird mehr Gas gegeben, um wieder auf die Sollgeschwindigkeit von 80 km/h zu kommen.
http://www.roboternetz.de/wiki/uploads/Main/Regelkreis3.gif
Um nun diese Aufgabe technisch zu lösen, gibt es die Regelungstechnik. Sie baut im wesentlichen auf die mathematische Beschreibung und Modellbildung des Systems Regelkreis. Zur Modellierung, Beschreibung und Simulation werden Blockschaltbilder mit diskreten Signalgliedern verwendet.
Ein vereinfachtes Blockschaltbild eines Regelkreises, wie es oft in der Regelungstechnik verwendet wird, ist in der nachfolgenden Abbildung dargestellt. Ein Regelkreis besteht entsprechend der Abb. aus den Hauptteilen Regler und Regelstrecke.
http://www.roboternetz.de/wiki/uploads/Main/Regelkreis4.gif
Regler: Ist der Teil des Regelkreises, der unter Berücksichtigung der dynamischen Eigenschaften der Regelstrecke aus der Regelabweichung die Korrekturmaßnahmen zum Ausregeln ergreift.
Regelstrecke: Ist der Teil des Regelkreises, der vom Regler ausgeregelt werden soll.
Führungsgröße (Sollwert) w: Vorgegebener Wert, auf dem die Regelgröße durch die Regelung gehalten werden soll. Sie ist eine von der Regelung nicht beeinflusste Größe und wird von außen zugeführt.
Regelgröße (Istwert) x: Ist die Ausgangsgröße der Regelstrecke, die zum Zweck des Regelns erfasst und zum Vergleich rückgeführt wird. In vielen Fällen ist in der Rückführung noch eine Messeinrichtung (Sensor) gezeichnet, die den Istwert erfasst, hier der Einfachheit halber weggelassen.
Regelabweichung e: Differenz zwischen Führungsgröße und Regelgröße e = w - x, bildet die eigentliche Eingangsgröße des Reglers.
Stellgröße y: Ausgangsgröße der Regeleinrichtung und zugleich Eingangsgröße der Strecke. Sie überträgt die steuernde Wirkung des Reglers auf die Strecke.
Störgröße z: Eine von außen wirkende Größe, die eine Änderung des Istwertes der Regelgröße bewirkt und einen Regelvorgang auslöst.
Die Regelstrecke
Die Regelstrecke stellt den zu regelnden Teil bzw. den zu regelnden Prozess dar und umfasst normalerweise eine Reihe von einzelnen Gliedern. Die Glieder werden entsprechend ihrem Zeitverhalten charakterisiert. Um das Zeitverhalten herauszufinden, legt man an den Eingang ein Testsignal an und zeichnet die Antwort auf. Im einfachsten Fall wird der Eingang mit einer sprunghaften Änderung beaufschlagt. Die Antwort auf die sprunghafte Änderung der Eingangsgröße wird Sprungantwort genannt und gibt Aufschluss über die Art der Regelstrecke und kann eventuell bereits genutzt werden, um die Parameter der Regelstrecke zu bestimmen.
Für den Aufbau eines gut funktionierenden Regelkreises und die Auslegung von Reglern ist es eine Voraussetzung zu wissen, wie die Regelstrecke reagiert. Ohne ein genaues Wissen um das dynamische Verhalten der Regelstrecke ist es nicht möglich geeignete Regler auszuwählen und diese zu parametrieren.
Die wichtigsten dynamischen Grundelemente zur Charakterisierung der Regelstrecke sind nachfolgend aufgelistet. Jedes Element wird mit einem Block dargestellt und darin durch ein Symbol oder der stilisierten Sprungantwort gekennzeichnet.
Proportionalglied (P-Glied)
http://www.roboternetz.de/wiki/uploads/Main/pglied.gif
Die einfachste Art einer Regelstrecke.
Beispiel: Hebel, Getriebe, Verstärker, Spannungsteiler,
Sensoren bei denen das Zeitverhalten vernachlässigt werden kann
Integrator (I-Glied)
http://www.roboternetz.de/wiki/uploads/Main/iglied.gif
Strecke ohne Ausgleich, ist häufig in Regelstrecken vorhanden.
Beispiel: Beschleunigung -> Geschwindigkeit -> Weg,
Strom -> Kondensatorspannung
Verzögerungsglied 0.Ordnung (Totzeitglied)
http://www.roboternetz.de/wiki/uploads/Main/ttglied.gif
Entsteht durch Laufzeiten von Material oder Signalen. Je größer die Totzeit einer Regelstrecke ist, um so schwieriger ist sie zu regeln.
Beispiel: Förderband, Rechenzeit, A/D-Wandler
Verzögerungsglied 1.Ordnung (PT1-Glied)
http://www.roboternetz.de/wiki/uploads/Main/pt1glied.gif
Viele einfache Regelstrecken haben ein solches Verhalten bzw. können näherungsweise damit beschrieben werden. Ist ein P-Glied mit nicht vernachlässigbarem Zeitverhalten.
Beispiel: Gleichstrommotor (Spannung -> Drehzahl),
Widerstand-Kondensator-Schaltung (RC-Glied)
Verzögerungsglied 2.Ordnung (PT2-Glied)
Man unterscheidet schwingungsfähige und nicht schwingungsfähige PT2-Glieder. Zur Charakterisierung gibt es die Parameter Dämpfung D und Eckfrequenz w0 oder die Zeitkonstanten T1 und T2. Für Dämpfung D<1 ist es schwingungsfähig.
Schwingfähiges PT2-Glied:
http://www.roboternetz.de/wiki/uploads/Main/pt2aglied.gif
Beispiel: Mechanischer Schwinger (Feder-Masse-System),
elektrischer Schwingkreis (RLC-Kreis)
Nicht schwingfähiges PT2-Glied:
http://www.roboternetz.de/wiki/uploads/Main/pt2bglied.gif
Beispiel: Zwei hintereinander geschaltete PT1-Glieder
Der Regler
Der Regler hat die Aufgabe, die Regelgröße zu messen, sie mit dem Sollwert zu vergleichen und bei Abweichungen die Stellgröße so zu verändern, dass Soll- und Istwert der Regelgröße wieder übereinstimmen bzw. die Differenz minimal wird.
Die Wahl eines bestimmten Reglertyps richtet sich nach dem geforderten Zeitverhalten und der geforderten Regelgenauigkeit der Regelstrecke. Nachfolgend finden Sie eine Zusammenfassung der wichtigsten klassischen Reglertypen:
P-Regler
Der proportionalwirkende Regler multipliziert die Regelabweichung mit seinem Verstärkungsfaktor Kp und gibt das Ergebnis unverzögert weiter. Er unterscheidet sich prinzipiell nicht vom dynamischen Element P-Glied, ist nur eben künstlich hergestellt für den Einsatz als Regler. Der P-geregelte Kreis ist einfach und mittelschnell im Vergleich zu anderen Regelungen. Das Problem ist die bleibende Regelabweichung!
http://www.roboternetz.de/wiki/uploads/Main/pregler.gif
Software P-Regler:
y = Kp * e
I-Regler
Der integralwirkende Regler summiert die Regelabweichung über der Zeit auf und multipliziert die Summe (d.h. das Integral) mit dem Faktor Ki. Je länger eine Regelabweichung ansteht, desto größer wird die Stellgröße des I-Reglers. Er unterscheidet sich prinzipiell nicht vom dynamischen Element I-Glied, ist nur eben künstlich hergestellt für den Einsatz als Regler. Der I-geregelte Kreis ist langsam im Vergleich zu anderen Regelungen. Er hat aber den Vorteil, dass die Abweichung vollständig eliminiert wird.
http://www.roboternetz.de/wiki/uploads/Main/iregler.gif
Software I-Regler:
esum = esum + e y = Ki * Ta * esum
esum ist die Summe aller bisherigen Abweichungen e. Der Parameter des Software I-Reglers ist abhängig von der Rechenschrittweite Ta (Abtastzeit). Je öfter gerechnet wird, desto öfter wird auch hinzugezählt (aufintegriert). Eine kleine Abtastzeit erfordert also einen kleineren Faktor, dies wird durch die Multiplikation mit Ta verwirklicht.
PI-Regler
Der PI-Regler ist die Kombination aus P- und I-Regler und kombiniert den Vorteil des P-Reglers, nämlich schnelle Reaktion, mit dem Vorteil des I-Reglers, der exakten Ausregelung. Der PI-geregelte Kreis ist also genau und mittelschnell.
http://www.roboternetz.de/wiki/uploads/Main/piregler.gif
Software PI-Regler:
esum = esum + e y = Kp * e + Ki * Ta * esum
PD-Regler
Der proportional-differential wirkende Regler kombiniert den P-Regler mit einem D-Anteil. Der D-Anteil bewertet die Änderung einer Regelabweichung (er differenziert) und berechnet so deren Änderungsgeschwindigkeit. Diese wird mit dem Faktor Kd multipliziert und zum P-Anteil hinzuaddiert. Der PD-Regler reagiert damit schon auf Ankündigungen von Veränderungen, das bewirkt sozusagen ein Vorhalten beim Regeln.
Der PD-geregelte Kreis ist sehr schnell im Vergleich zu anderen Regelungen, und manche Regelkreise (solche mit zweifacher Integration) sind ohne D-Anteil überhaupt nicht stabilisierbar. Das Problem der proportionalen Regler, die bleibende Regelabweichung, ist beim PD-Regler allerdings weiterhin vorhanden!
Ein Nachteil aller Regler mit D-Anteil kann die Unruhe im Kreis sein. Ist das Sensorsignal verrauscht, so wird dieses Rauschen durch die Differenziation weiter verstärkt und wieder in den Kreis hineingegeben. Dadurch wird der Aktuator stärker belastet. Macht der Regler insbesondere sehr hohe Ausschläge als Folge von schnellen Änderungen des Sollwertes, dann kann es sein, dass das Stellglied oder der Aktuator diese nicht umsetzen kann - die Wirkung des D-Anteils würde dann durch die Begrenzung verpuffen, und das Einschwingverhalten wäre nicht wie berechnet, sondern meist langsamer. Dies gilt aber nur für große Sprünge. Bei den normalen kleinen Regelvorgängen zum Ausgleich von Störeinflüssen wirkt der D-Anteil wie beabsichtigt.
http://www.roboternetz.de/wiki/uploads/Main/pdregler.gif
Software PD-Regler:
y = Kp * e + Kd * (e – ealt)/Ta ealt = e
Mit der neuesten Regelabweichung e und der vorhergehenden ealt wird der D-Anteil berechnet. Die Differenziation erfolgt damit angenähert durch Bildung des Differenzquotienten (e - ealt)/Ta.
PID-Regler
Der PID Regler ist der universellste der klassischen Regler und vereinigt die guten Eigenschaften der anderen Regler. Zur Beschreibung der Eigenschaften des P-, I- und D-Anteils siehe die anderen Reglertypen. Der PID-geregelte Kreis ist genau und sehr schnell. In den meisten Anwendungen kommt deshalb der PID-Regler zum Einsatz.
http://www.roboternetz.de/wiki/uploads/Main/pidregler.gif
Software PID-Regler:
esum = esum + e y = Kp * e + Ki * Ta * esum + Kd * (e – ealt)/Ta ealt = e
Alternative PID-Reglerstruktur:
Es gibt 2 Darstellungsmöglichkeiten, die inhaltlich identisch sind. In der analogen Regeltechnik ist noch die Darstellung mit der Nachstellzeit Tn und der Vorhaltezeit Tv üblich. Die Umrechnung zwischen den beiden Strukturen ist mit den angegebenen Formeln möglich.
Vergleich der Reglertypen
In der folgenden Abbildung ist der Vergleich von P-, I-, PI-, PD- und PID-Regler in einem Regelkreis mit PT2-Glied als Regelstrecke dargestellt. Es ist deutlich zu sehen, dass die Regler ohne I-Anteil (P und PD) eine bleibende Regelabweichung aufweisen. Erst die Regler mit I-Anteil können auf den Endwert von 1 ausregeln. Beim reinen I-Regler geht das so langsam, dass es gar nicht mehr auf dem Diagramm zu sehen ist. Der Hauptzweck eines I-Anteils ist also die Vermeidung bleibender Regelabweichungen. Daher ist ein I-Anteil normalerweise nicht nötig, wenn die Strecke schon einen I-Anteil besitzt. Ausnahme: Es wird ein doppelter I-Anteil zur Vermeidung von Schleppfehlern benötigt.
Die schnellsten Regler sind die mit einem D-Anteil (PD und PID). Der D-Anteil kommt deshalb hauptsächlich zum Einsatz, wenn schnelle Dynamik gefragt ist oder die Strecke selbst schon instabil ist. Voraussetzung für die Schnelligkeit ist allerdings, dass keine Begrenzung im Stellglied oder Aktuator auftritt. In der Praxis ist eine Begrenzung meistens nicht zu vermeiden, deshalb gilt die Sprungantwort in der Praxis nur für kleine Sprünge.
Die Regler ohne D-Anteil, aber mit P-Anteil (P und PI) sind mittelschnell. Für einfache Regelaufgaben reicht auch oft schon ein reiner P-Regler aus, wenn die bleibende Regelabweichung vernachlässigt werden kann oder weil die Strecke schon einen I-Anteil besitzt.
http://www.roboternetz.de/wiki/uploads/Main/vergleich.gif
Aus diesem Vergleich wird klar, warum der PID-Regler so beliebt ist, er vereinigt die Vorzüge aller anderen Regler.
Digitaler Regler
Durch die Einführung leistungsfähiger und preiswerter Mikroprozessoren hat sich der digitale Regler mehr und mehr durchgesetzt. Im Gegensatz zum analogen Regler werden die Signale nicht mehr analog mit Operationsverstärker verarbeitet, sondern mit einem Mikroprozessor errechnet. Bevor das Signal vom Mikroprozessor bearbeitet werden kann, muss zunächst das Eingangssignal (Istwert) mit einem Analog-Digital-Umsetzer (ADU) digitalisiert werden, d.h. in einen Zahlenwert umgewandelt werden. Das vom digitalen Regler errechnete Ausgangssignal (Stellgröße) wird wiederum zur Ansteuerung des Stellglieds mit einem Digital-Analog-Umsetzer (DAU) in ein analoges Signal gewandelt. Funktionell unterscheiden sich analoger und digitaler Regler jedoch nicht wesentlich, es müssen nur die Schnittstellen angepasst werden.
http://www.roboternetz.de/wiki/uploads/Main/digreg.gif
Da die Wandlungen und das Regelprogramm eine gewisse Zeit beanspruchen, vergeht pro Durchlauf die sogenannte Takt- oder Abtastzeit. Diese Zeit wirkt sich im Regelkreis wie ein Totzeitglied mit der halben Abtastzeit als Totzeit aus. Das verursacht eine zusätzliche Phasenverschiebung, was sich ungünstig auf die Stabilität des Regelkreises auswirken kann. Ist die Abtastzeit sehr viel kleiner als die dominierende Zeitkonstante der Strecke, dann spricht man von quasi-kontinuierlichem Verhalten, da sich der digitale Regler ähnlich wie ein analoger Regler verhält. Der digitale Regler kann dann wie ein analoger dimensioniert werden. Ist die Abtastzeit größer, kann sie nicht mehr vernachlässigt werden, dann muss sie auch beim Reglerentwurf berücksichtigt werden.
Vorteile digitaler Regler:
- Die Verarbeitung erfolgt driftfrei.
- Es lassen sich nichtlineare Kennlinien, intelligentes Verhalten oder adaptive Regelung leichter realisieren.
- Der Regler kann bei Bedarf per Software neu konfiguriert und parametriert werden
Digitale Realisierung am Beispiel des PID-Algorithmus
Ausgehend von der Differentialgleichung für kontinuierliche Systeme wird die Differenzengleichung für zeitdiskrete Systeme erstellt. Daraus folgt dann der Stellungsalgorithmus in allgemeiner Form.
Ta = Abtastzeit; k = Nummer der Abtastung
Kp = Proportionalbeiwert; Ki = Integrierbeiwert; Kd = Differenzierbeiwert
Differentialgleichung für den kontinuierlichen PID-Regler:
- [math] y(t) \;=\; Kp \!\cdot\! e(t) + Ki \int_0^t e(\tau) \, d\tau + Kd \, \frac{de(t)}{dt} [/math]
Differenzengleichung für den zeitdiskreten PID-Regler:
- [math] y_k \;=\; Kp \!\cdot\! e_k + Ki \!\cdot\! Ta \sum_{i=0}^k e_i + \frac{Kd}{Ta}\, ( e_k - e_{k-1} ) [/math]
PID Stellungs-Algorithmus:
- [math] y_k \;=\; y_{k-1} + q_0 \!\cdot\! e_k + q_1 \!\cdot\! e_{k-1} + q_2 \!\cdot\! e_{k-2} [/math]
Mit den Parametern:
- [math] q_0 \,=\, Kp + Ki \!\cdot\! Ta + \frac{Kd}{Ta} \, , \quad q_1 \,=\, -Kp - 2 \, \frac{Kd}{Ta} \, , \quad q_2 \,=\, \frac{Kd}{Ta} [/math]
Umsetzung in Code nach der Differenzengleichung:
Im Code wurden einige Variablen umbenannt, da die Indexschreibweise nicht möglich ist.
y entspricht yk, e entspricht ek, ealt entspricht ek-1, esum ist die Summenbildung
In der Praxis wird man die Ausdrücke Ki*Ta und Kd/Ta vorab berechnen und mit Ersatzvariablen in die Reglergleichung einsetzen. Der Verständlichkeit halber wurde es hier im Code belassen. Des weiteren kann eine Begrenzung von esum notwendig werden, um einen Variablenüberlauf oder Windup-Effekt zu vermeiden.
Der nachfolgende Code wird im Rhythmus der Abtastzeit Ta immer wieder aufgerufen.
e = w - x; //Vergleich esum = esum + e; //Integration I-Anteil y = Kp*e + Ki*Ta*esum + Kd/Ta*(e – ealt); //Reglergleichung ealt = e;
Alternative Umsetzung in Code nach dem Stellungsalgorithmus:
y entspricht yk, yalt entspricht yk-1, e entspricht ek, ealt entspricht ek-1, ealt2 entspricht ek-2
e = w - x; //Vergleich y = yalt + q0*e + q1*ealt + q2*ealt2; //Reglergleichung ealt2 = ealt; ealt = e; yalt = y;
Dimensionierung des Reglers
Die Auswahl des Reglertyps ist heutzutage bei den digitalen Reglern nicht mehr so kritisch, da der Mehraufwand in Software für einen PID-Regler gegenüber einfacheren Typen kaum zu Buche schlägt. Im Prinzip ist man deshalb mit einem PID-Regler fast immer auf der richtigen Seite, mit einer Ausnahme, bei einer Strecke mit reiner Totzeit. Die folgende Tabelle zeigt die Wahlmöglichkeiten.
| Strecke | Regler
| |||
P
|
PD
|
PI
|
PID
| |
| reine Totzeit | geeignet
|
|||
| 1.Ordnung mit kleiner Totzeit | gut geeignet | gut geeignet | ||
| 2.Ordnung mit kleiner Totzeit | gut geeignet | |||
| höhere Ordnung | gut geeignet | |||
| I-Glied und Verzögerung | geeignet | gut geeignet | geeignet
|
gut geeignet |
Nachdem man einen geeigneten Reglertyp ausgewählt hat, stellt sich noch die Frage, wie man die Reglerparameter Kp, Ki, und Kd optimiert. Im Laufe der Zeit wurden viele Methoden zur Dimensionierung der Reglerparameter entwickelt. Diese Aufzählung beschränkt sich auf die einfacheren und gängigen Methoden der Parametrierung.
Dimensionierung durch Probieren (Empirisches Einstellen)
Diese Methode ist geeignet um einfache Systeme zu dimensionieren, insbesondere wenn man bereits Erfahrung mit ähnlichen Regelkreisen hat. Man fängt mit einer unkritischen Einstellung (Kp klein, Ki=0, Kd=0) an und erhöht langsam die Verstärkung Kp, bis die Dämpfung schlecht wird. Falls eine Schwingneigung auftritt, muss die Verstärkung wieder etwas zurück genommen werden. Dann nimmt man allmählich den Integralanteil hinzu, erhöht ihn in Schritten und probiert solange herum, bis das Ergebnis einigermaßen passt. Bei Bedarf kann noch ein D-Anteil (PID-Struktur) probiert werden. Wenn dabei die Regelung stabiler wird, kann noch mal Kp und Ki erhöht werden, bis man endgültig zufrieden ist.
Es dürfte klar sein, dass so eine Optimierung im Blindflug nicht immer das Optimum ergibt, aber es ist eine gängige praktische Methode zur Ermittlung der Reglerparameter. Besser sieht es aus, wenn in einer Simulation empirisch optimiert wird. Zusätzliche Informationen über die Stabilität erlauben hierbei eine gezieltere Optimierung. Dazu muss allerdings die Regelstrecke bekannt sein. Ist das nicht der Fall, so bleibt nur das einfache Probieren oder das Einstellen nach der Schwingungsmethode wie im folgenden beschrieben.
Dimensionierung nach Einstellregeln
Die Dimensionierung nach Rezept ist eine praktische Methode ohne viel Rechnerei und Hilfsmittel, eine Methode also für den Praktiker. Die bekanntesten Einstellregeln sind von Ziegler/Nichols und von Chien/Hrones/Reswick. Darüber hinaus gibt es noch eine Vielzahl anderer Einstelltabellen, auf die hier aber verzichtet wird, das würde den Rahmen dieses Artikels sprengen. An der Vielzahl kann man schon ersehen, dass es kein universell gültiges Rezept gibt und mit diesen Tabellen nicht unbedingt das Optimum erreicht wird, eine Nachoptimierung kann nötig sein.
Bei Ziegler/Nichols unterscheidet man noch zwischen der Schwingungsmethode und der Einstellung nach der Sprungantwort.
Einstellung nach der Schwingungsmethode:
Bei der Schwingungsmethode nach Ziegler/Nichols werden die Regelparameter so verstellt, dass die Stabilitätsgrenze erreicht wird und der Regelkreis zu schwingen beginnt, d.h. die Regelgröße periodische Schwingungen ausführt. Aus der so gefundenen Einstellung können die Reglerparameter ermittelt werden. Dieses Verfahren ist nur auf Regelstrecken anwendbar, bei denen ein Schwingen keinen Schaden anrichtet und die überhaupt instabil gemacht werden können. Die Vorgehensweise ist folgende:
- Einstellung des Reglers als reinen P-Regler: Ki = 0 und Kd = 0
- Die Reglerverstärkung Kp wird solange vergrößert, bis sich der geschlossene Regelkreis an der Stabilitätsgrenze befindet und Dauerschwingungen ausführt.
- Der dabei eingestellte Wert Kp wird als Kpkrit bezeichnet.
- Die Periodendauer der sich einstellenden Dauerschwingung Tkrit wird gemessen.
- Anhand der folgenden Tabelle werden dann die Reglerparameter bestimmt.
|
|
Der Vorteil dieses Verfahrens liegt darin, dass die Untersuchung während des Betriebes und ohne Öffnen des Regelkreises durchgeführt werden kann. Der Nachteil an dem Verfahren ist, dass es nur auf Strecken angewendet werden kann, die auch zum Schwingen gebracht werden können.
Einstellung nach der Sprungantwort:
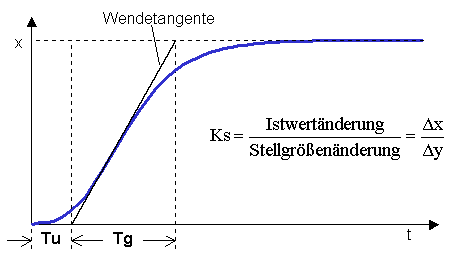
Diese Methode der Parameterbestimmung beruht auf der Aufnahme der Sprungantwort der Regelstrecke. Es eignet sich auch für Strecken, die nicht zum Schwingen gebracht werden können. Der Regelkreis muss allerdings geöffnet werden.
Vorgehensweise: Es wird die Sprungantwort aufgenommen und durch Einzeichnen der Wendetangente die Verzugszeit Tu und die Ausgleichszeit Tg ermittelt.
Mit den so festgestellten Werten werden die Parameter für den einzusetzenden Regler gemäß nachstehenden Tabellen ermittelt.
|
|
|
|
Dimensionierung mit dem Bodediagramm
Ein Bode-Diagramm ist die grafische Darstellung des Frequenzganges. Es werden der Betrag der Übertragungsfunktion (Amplitudengang) und der Verlauf des Phasenwinkels (Phasengang) als Funktion der Frequenz aufgetragen. Die Frequenzachse und die Amplitudenachse werden logarithmisch dargestellt. Die logarithmische Darstellung hat den Vorteil, dass eine Multiplikation auf eine einfache Addition zurückgeführt wird. Somit wird eine Hintereinanderschaltung von Systemen im Blockschaltbild zu einer einfachen Addition im Bodediagramm.
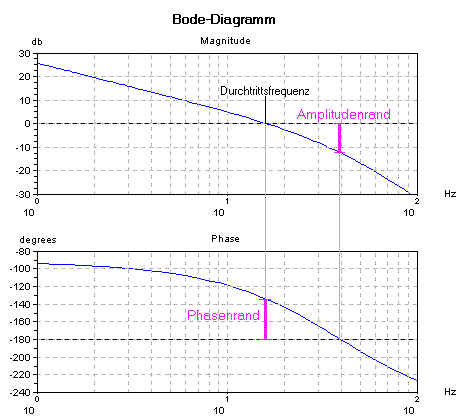
Das Zeitverhalten des rückgekoppelten Regelkreises hängt entscheidend vom Verlauf des Frequenzganges der offenen Regelschleife in der Umgebung des Durchtretens durch die 0dB-Achse ab. In der Regelungstechnik wird daher der offene Regelkreis im Bode-Diagramm aufgetragen. Das erlaubt einen schnellen Überblick über Stabilität und möglichen Reserven zur Optimierung. Ein Kriterium für die Stabilität der Schleife ist der Phasenrand und der Amplitudenrand. Der Phasenrand ist der Abstand (Phasenreserve) zur –180°-Linie bei der Durchtrittsfrequenz. Die Durchtrittsfrequenz ist diejenige Frequenz, bei der der Amplitudengang durch die 0dB-Linie geht. Siehe auch folgendes Bode-Diagramm.
| Regel: Eine geschlossene Regelschleife arbeitet genau dann stabil, wenn der Phasenrand positiv ist. |
Wird diese Bedingung verletzt, so wird in diesem Frequenzbereich die im Rückführzweig der Regelung eingebrachte Gegenkopplung zu einer Mitkopplung und das System kann schwingen.
Beim Reglerentwurf sind folgende Punkte zu beachten:
- Der Phasenrand muss positiv sein. Der geschlossene Regelkreis kann sonst instabil sein.
- Je größer der Phasenrand ist, desto größer ist die Stabilitätsreserve des Regelkreises und desto höher ist die Dämpfung des Regelkreises. Üblich sind Werte von 40°...70° für gutes Führungsverhalten und 20°...50° für gutes Störverhalten.
- Die Durchtrittsfrequenz ist ein Maß für die Schnelligkeit des Regelkreises, je höher, desto schneller ist die Reaktion auf Änderungen der Führungsgröße oder Störungen.
Hier ein Beispiel zur Dimensionierung mit dem Bode-Diagramm.
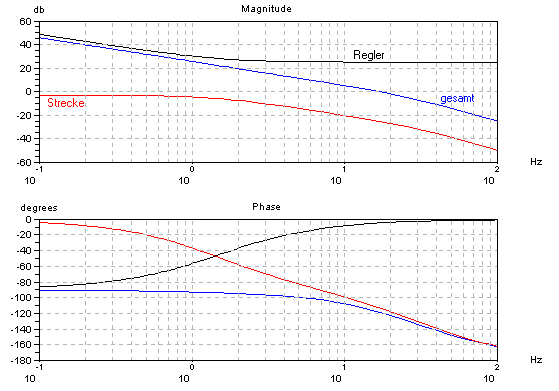
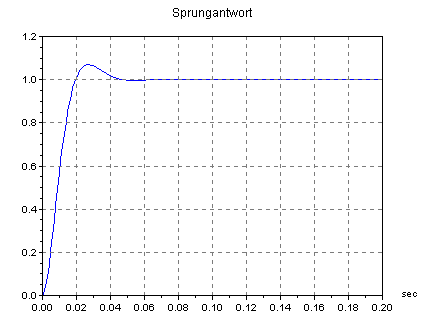
Die Strecke ist rot dargestellt und besteht in dem Beispiel aus einem nicht schwingfähigem PT2-Glied. Man sucht sich den Punkt, wo die Strecke für sich alleine noch ausreichend Phasenreserve hat, z.B. 70°. In dem Beispiel also die Frequenz, bei der die Strecke –110° Phasendrehung aufweist. Das ist etwa bei 15Hz. Da hat die Strecke ungefähr eine Dämpfung von 25dB. Wenn man nun diese Dämpfung durch eine Verstärkung von 25dB kompensiert, dann wird dieser Punkt zur Durchtrittsfrequenz. D.h. man wählt den P-Anteil des Reglers Kp=18, denn 25dB entspricht ungefähr dem Faktor 18. Um die Regelabweichung zu minimieren, wird noch ein I-Anteil hinzugefügt. Üblicherweise wählt man für die Grenzfrequenz des PI-Reglers die Grenzfrequenz des dominierenden Streckenteils, in dem Beispiel ca. 1.4Hz. Damit ergibt sich ein I-Anteil von 170. Im Bode-Diagramm ist der PI-Regler als schwarze Kurve eingezeichnet. Die Addition der Strecke und des Reglers im Bode-Diagramm führt dann zum Frequenzgang des offenen Regelkreises (blaue Kurve). Die resultierende Durchtrittsfrequenz ist wie gewählt bei etwa 15Hz. Der Phasenrand hat sich durch den I-Anteil im Regler auf ca. 60° reduziert, ist aber noch ausreichend. Das Einschwingen des geschlossenen Regelkreises für diese Dimensionierung sieht dann folgendermaßen aus:
Bei Bedarf könnte noch ein D-Anteil (PID-Regler) hinzugenommen werden, das würde die Phase anheben und man könnte dadurch die Durchtrittsfrequenz weiter nach oben schieben. In der Praxis wird dies allerdings wegen der wahrscheinlichen Begrenzung des Stellglieds kein schnelleres Einschwingen mehr bringen.
Begrenzungen oder Nichtlinearitäten werden bei der Dimensionierung mit dem Bode-Diagramm nicht berücksichtigt. Das ist ein Nachteil dieser Methode. Eventuell muss deshalb noch einmal im Zeitbereich nachoptimiert werden.
Beispiel: Drehzahlregelung
Es soll ein Gleichstrommotor in der Drehzahl geregelt werden. Als Sensor ist ein Tachogenerator vorhanden, der direkt auf der Motorwelle sitzt. Das System ist in einem kleinen Modellfahrzeug eingebaut und wird zur Geschwindigkeitsregelung eingesetzt, da die Drehzahl proportional zur Geschwindigkeit ist.
Das Funktionsschaltbild sieht folgendermaßen aus: http://www.roboternetz.de/wiki/uploads/Main/drehzahl1.gif
Als Störgröße können unterschiedliche Reibwerte oder Steigung und Gefälle rückwirkend über das Getriebe die Drehzahl beeinflussen. Das Getriebe und die Last sind zwar außerhalb der Regelschleife, beeinflussen aber durch die feste Kopplung des Getriebes die Dynamik des Regelkreises. Durch die starre Kopplung kann das Trägheitsmoment des Motors und die Masse des Fahrzeugs zusammengefasst werden. Das Gleiche gilt auch für die Reibwerte. Damit vereinfacht sich die Modellierung und das Blockschaltbild reduziert sich auf folgende Schaltung:
http://www.roboternetz.de/wiki/uploads/Main/drehzahl2.gif
Zur Ermittlung des dynamischen Verhaltens der Regelstrecke wird die Sprungantwort gemessen. Dazu wird auf den Eingang der Regelstrecke (Stellglied) ein Spannungssprung gegeben und die Antwort am Ausgang des Tachogenerators nachgemessen. Diese Methode erspart die aufwändige Ermittlung der elektrischen und mechanischen Daten der einzelnen Elemente der Regelstrecke (Motor, Getriebe, Fahrzeug). Die Sprungantwort der Regelstrecke ist in der nächsten Abbildung zu sehen:
http://www.roboternetz.de/wiki/uploads/Main/tacho.gif
Wie zu erwarten, ist die Sprungantwort annähernd ein Verzögerungsglied 1.Ordnung. Die abgelesene Zeitkonstante ist 0.11s. Die Verstärkung der Regelstrecke ist Ks = 0.72. Das Übertragungsmaß des Tachogenerators ist 1V pro 2480Upm. Damit kann auf die Drehzahl rückgerechnet werden.
Da die Regelstrecke nur aus einem PT1-Glied besteht, könnte eine analoge Regelung fast beliebig schnell gemacht werden. Wegen der Begrenzung bringt aber das Ausreizen der Optimierung für das Führungsverhalten nicht viel, nur für das Störverhalten wäre eine schnellere Regelung sinnvoll. Um aber einen Vergleich zwischen analogem und digitalem Regler anstellen zu können wird eine Parametrierung gewählt, die auch für den digitalen Regler mit seiner Totzeit noch stabil ist. Es wird deshalb auch auf einen D-Anteil im Regler verzichtet und nur ein PI-Regler realisiert. Das vereinfachte Blockschaltbild mit den dynamischen Elementen sieht damit folgendermaßen aus:
http://www.roboternetz.de/wiki/uploads/Main/drehzahl3.gif
Die Parameter des PI-Reglers sind: Kp = 18; Ki = 200
Die Werte wurden empirisch in einer Simulation ermittelt. Die Sprungantwort des Regelkreises sieht damit folgendermaßen aus:
http://www.roboternetz.de/wiki/uploads/Main/tacho2.gif
Realisierung mit analogem Regler
Die Realisierung als elektrische Schaltung ist in der nächsten Abbildung zu sehen. Der erste Operationsverstärker vergleicht den Sollwert w mit dem Istwert x. Der zweite Operationsverstärker bildet den PI-Regler. Die Werte R5, R6 und C1 sind so gewählt, dass sich die Parameter Kp = 18 und Ki = 200 ergeben. Die Formeln dazu sind:
Kp = R6/R5
Ki = 1/(R5*C1)
Da die Schaltung des PI-Reglers invertiert, wurden zum Ausgleich am Vergleicher die Eingänge w und x vertauscht, so dass sich über die gesamte Schaltung wieder die richtige Polarität ergibt.
http://www.roboternetz.de/wiki/uploads/Main/drehzahlregler.gif
Realisierung mit digitalem Regler
Bei der Realisierung mit einem digitalem Regler wird der Istwert x vom Tachogenerator mit einem A/D-Wandler digitalisiert. Der Sollwert w wird dem µC als digitaler Wert übergeben. Die Stellgröße y entspricht dem PWM-Wert für den Motortreiber. Um zum analogen Regler vergleichbar zu sein, wurde sowohl für den A/D-Wandler als auch für den PWM-Steller eine 8-Bit-Breite vorgesehen. Damit ist die Verstärkung in beiden Fällen gleich und analoger und digitaler Regler gut vergleichbar.
In dem folgenden Programmbeispiel ist als Programmiersprache C gewählt. Da der Code sehr einfach ist, sollte es kein Problem sein, den Code auf andere Sprachen umzusetzen. Der Algorithmus wird alle 10ms aufgerufen, d.h. die Taktzeit Ta = 10ms. In der Reglergleichung kann zur Vereinfachung das Produkt Ki*Ta durch eine Ersatzvariable, die gleich das Ergebnis aus dem Produkt 200*0.01 = 2 hat, ersetzt werden. Zum besseren Verständnis wurde es hier beim Ki*Ta belassen. Um einen Windup-Effekt zu verhindern, wird die Summenbildung esum auf 128 begrenzt. Der Wert wurde so gewählt, dass noch eine volle Aussteuerung durch den I-Anteil möglich ist. Zum Schluss wird die Stellgröße y auf die mögliche Aussteuerung des Stellglieds (0...255) begrenzt.
Programmbeispiel digitaler PI-Regler:
e = w - x; //Vergleich
esum = esum + e; //Integration I-Anteil
if (esum < -128) {esum = -128;} //Begrenzung I-Anteil
if (esum > 128) {esum = 128;}
y = Kp*e + Ki*Ta*esum; //Reglergleichung
if (y < 0) {y = 0;} //Begrenzung Stellgröße
if (y > 255) {y = 255;}
PWM = y; //Übergabe Stellgröße
Autor Waste