(→Einatzmöglichkeiten) |
|||
| (49 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
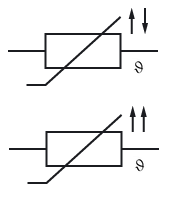
[[Bild:Schaltzeichen_ntcptc.PNG|thumb|Schaltzeichen eines NTC (oben) und eines PTC (unten)]] | [[Bild:Schaltzeichen_ntcptc.PNG|thumb|Schaltzeichen eines NTC (oben) und eines PTC (unten)]] | ||
| − | + | Heißleiter (engl. '''NTC''', ''negative temperature coefficient'') und Kaltleiter (engl. '''PTC''', ''positive temperature coefficient'') sind elektrische Widerstände aus bestimmten Materialien, deren Leitfähigkeit (und damit der Widerstand) sich mit der Temperatur deutlich ändert. | |
| + | ==NTCs== | ||
| + | [[Bild:ntc.gif|thumb|Typische Bauform]]Heißleiter sind stromleitende Materialien, die bei hohen Temperaturen eine höhere Leitfähigkeit besitzen als bei tiefen Temperaturen. Sie haben einen negativen Temperaturkoeffizienten; das heißt, mit steigender Temperatur sinkt ihr elektrischer Widerstand. | ||
| + | Ein großer Vorteil ist die starke Temperaturabhängigkeit und der geringe Preis. | ||
| + | Das nichtlineare Verhalten des Widerstandswertes bei sich verändernder Temperatur ist jedoch zugleich auch der größte Nachteil. | ||
| + | Ein einzelner, nicht kompensierter NTC ändert seinen Widerstand nicht linear. Hier dazu ein Beispieldiagramm: | ||
| − | + | [[Bild:ntcdiagramm.gif]] | |
| − | + | ||
| − | |||
| − | |||
| − | + | ===Temperaturabhängigkeit=== | |
| − | + | Mithilfe eines NTCs lässt sich ein einfacher Temperatursensor bauen. | |
| + | Bildet der Heißleiter einen Spannungsteiler mit einem konstanten Widerstand, so lässt sich die geteilte Spannung mithilfe eines Microcontrollers messen, wodurch auf den Widerstand des NTCs geschlossen werden kann.<br /> | ||
| + | Der Heißleiter ändert seinen elektrischen Widerstand nicht linear. Jedoch kann die Temperatur auch rechnerisch ermittelt werden. Es gilt:<br/> | ||
| + | <pre> | ||
| + | T ~ 1/ln(R) | ||
| + | </pre> | ||
| + | Bei Einbeziehung der Aktivierungsenergie, der Nenntemperatur (meist 25°C), und des Nennwiderstandes bei Nenntemperatur | ||
| + | gilt folgende Funktion:<br /> | ||
| + | <pre> | ||
| + | T(R) = T_N * B / (B + T_N * ln(R / R_N)) | ||
| + | </pre> | ||
| + | Wobei '''T''' die momentane Temperatur, '''T_N''' die Nenntemperatur (in Kelvin), '''R''' der Widerstand des Heißleiters und '''R_N''' den Nennwiderstand darstellt. Bei '''B''' handelt es sich um eine Materialkonstante, die vom Herrsteller im Datenblatt angegeben wird. Bei Implementierung der Funktion in ein Programm für den Microcontroller müssen umbedingt die Datentypen berücksichtigt werden! | ||
| + | {{Ausbauwunsch|Erbitte Implementierung der Gleichungen (Unbekannter Parserfehler)}} | ||
==PTCs== | ==PTCs== | ||
| − | Kaltleiter | + | Kaltleiter sind stromleitende Materialien, die bei hohen Temperaturen eine niedrigere Leitfähigkeit besitzen als bei tiefen Temperaturen. Sie haben einen positiven Temperaturkoeffizienten; das heißt, mit steigender Temperatur steigt auch ihr elektrischer Widerstand. |
| − | + | Bei den PTCs gibt es zwei Sorten: Einmal welche mit näherungsweise linearer Kennlinie und dann welche mit stark nichtlinearer Kennlinie. Die linearen Typen (z.B. KTYxx Reihe) oder Platinwiderstände (z.B. PT100, PT1000 ) sind mehr für die Temperaturmessung gedacht. | |
| − | + | Recht beliebt sind die PTCs der KTYxx-Reihe z.B. der KTY81-110. Sie sind sehr günstig (ca. 0,50€) und bieten für die meisten Anwendungen eine ausreichende Genauigkeit. | |
| + | |||
| + | Für höhere Anforderungen an den Messbereich (je nach Typ von -260 ... 850 °C) oder die Genauigkeit gibt es Platin-Widerstände zur Temperaturmessung. Auch hier ist der Temperaturkoeffizient positiv (0,38 %/K bei Raumtemperatur). Am häufigsten findet man hier Widerstände von 100 Ohm (PT100) und 1000 Ohm (PT1000). Diese sind jedoch relativ teurer (je nach Typ und Bezugsquelle und Qualität ab etwa 3 €). | ||
| + | |||
| + | Die stark nichtlinearen Typen sind mehr als Übertemperaturschutz oder als selbst rückstellende Sicherung geeignet. | ||
| + | Auch dazu ein Beispieldiagramm für einen nicht linearen PTC: | ||
| − | |||
[[Bild:Ptcdiagramm.GIF]] | [[Bild:Ptcdiagramm.GIF]] | ||
| + | ==Einatzmöglichkeiten== | ||
| + | Mit NTCs und PTCs lassen sich in "normalen" Bereichen (das heißt hier kleiner etwa 200 °C) günstig Temperaturen messen. Dieses Gebiet umfasst alles vom kleinen digitalen Fieberthermometer über die verschiedenen Anzeigeinstrumente (wie Wetterstationen und KFZ-Elektronik) bis hin zu kompletten Heizungs- und Klimasteuerungen in Gebäuden. | ||
| − | + | Daneben gibt es auch Anwendungen bei denen es nicht um eine eigentliche Messung geht: | |
| + | *spezielle NTCs werden z.B. bei Netzteilen als Einschaltstrombegrenzer genutzt. Hier wird die Eigenerwärmung als gewollter Effekt genutzt: die Bauteile sind im kalten Zustand so hochohmig, dass beispielsweise große Elkos geladen werden, ohne dass die vorgeschaltete Sicherung auslöst. Fließt dann der Nennstrom, erwärmen sich die Bauteile und verringern ihren Widerstand. Um wieder strombegrenzend wirksam zu sein, müssen sie nach Abschalten des Gerätes erst abkühlen. | ||
| + | *PTC-Sicherungen schalten den Strom aufgrund ihrer Eigenerwärmung bei Überlastung ab. Sie sind gut für Verbraucher geeignet, die kurzzeitig Überlast vertragen (z.B. Transformatoren), da die Auslösung relativ träge ist. Erst nach Trennen der Stromversorgung stellen sich die PTC-Sicherungen durch Abkühlung zurück. Bei der Auswahl von PTC-Sicherungen muss neben Halte- und Abschaltstrom deren Maximalstrom und die Maximalspannung beachtet werden. | ||
| + | *PTC-Heizelemente können selbst ihre Temperatur regeln. Sie ist werkstoffabhängig. | ||
| + | ==Temperaturmessung mit PTC== | ||
| + | Um aus der Widerstandsänderung am Sensor eine passende Spannung zu erzeugen gibt es verschieden Möglichkeiten. Ein naheliegender Weg ist eine Konstantstromquelle, so dass die Spannung am Sensor direkt proportional zum Widerstand ist. Wenn man das Signal danach digitalisieren will, hat dieser Weg aber zwei wesentliche Nachteile: Eine gute Konstantstromquelle ist aufwendig, und man hat dann 2 Referenzen im System und damit unnötige Fehlerquellen. Für eine Widerstandsmessung ist ein Widerstand als Vergleichswert besser und einfacher als das Verhältnis von einer Spannungsquelle und einer Stromquelle. Dafür gibt es im wesentlichen 3 Möglichkeiten: | ||
| + | |||
| + | 1) Der selbe Strom fließt durch den Sensor und den Vergleichswiderstand. Die Spannung an Vergleichswiderstand wird als Referenz für den AD Wandler benutzt, die Spannung am Sensor wird gemessen. Dieses Verfahren ist vor allem mit hochauflösenden AD Wandlern mit Differenzeingängen (z.B. LTC2440) sinnvoll. | ||
| + | |||
| + | 2) Der selbe AD Wandler misst nacheinander die Spannung am Sensor und Vergleichswiderstand. Dafür braucht man 2 Eingänge mit Differenzeingang. | ||
| + | |||
| + | 3) Der Sensor und der Vergleichswiderstand bilden einen Spannungsteiler. Die Spannung über den Spannungsteiler dient als Referenz für den AD-wandler. Anders als bei den beiden vorherigen Möglichkeiten ist das Ergebnis der AD Wandlung hier nicht mehr linear vom Widerstand abhängig. | ||
| + | Bei einem kleinen Messbereich und geringer Auflösung des AD's lohnt es sich ggf. den konstanten Teil der Spannung abzuziehen, damit der Wertebereich des AD Wandler weitgehend ausgenutzt werden kann. Die Schaltung ist dann eine Brückenschaltung. | ||
| + | |||
| + | In allen 3 Fällen muss der Strom nicht besonders stabilisiert sein und es wird keine stabile Referenzspannung für den AD benötigt. Es kommt nur auf das Spannungsverhältnis an. | ||
| + | |||
| + | Beim Strom durch den Sensor muss ein Kompromiss zwischen genügend Spannung und der Eigenerwärmung des Sensors gefunden werden. Bei mehr als etwa 1 mW Verlustleistung am Sensor wird eine genaue Temperaturmessung schwierig. Für genaue Messungen mit dem PT100 werden oft sogar 0,1 mW als Grenze angegeben, d.h der Strom liegt bei nur 1 mA. | ||
| + | |||
| + | ==Linearisierung== | ||
| + | [[Bild:LinearPTC.GIF]] | ||
| + | KTY81 mit konstanten Strom (1,4 mA), und mit Widerstand in Reihe. | ||
| + | |||
| + | Um trotz der nicht linearen Kennlinie des Sensors ein linear von der Messgröße (Temperatur) abhängiges Ergebnis (Spannung oder Digitaler Wert) zu erhalten, bieten sich verschiedene Methoden an: | ||
| + | |||
| + | * Man nutzt die Nichtlineare Kennlinie von Dioden. Wegen der Temperaturabhängigkeit der Diodenkennlinie ist das aber schwierig und nur für sehr starke Nichtlinearitäten gerechtfertigt. Für die schwache Nichtlinearität der PTCs ist das Verfahren eher ungeeignet. | ||
| + | |||
| + | * Man nutzt den nichtlinearen Zusammenhang zwischen Spannung und Widerstand beim Spannungsteiler, bzw. in einer Brückenschaltung. Bei den Sensoren des Typs KTY81 wird mit einem 2,7kOhm-Widerstand in Reihe gerade eine relativ gute Kompensation der Nichtlinearitäten erreicht. Im Bereich von -40 °C ... +140 °C erscheint der PTC nun nahezu linear, der verbleibende Linearitätsfehler liegt bei etwa ±10 mV (für 5 V am Spannungsteiler). So einfach geht die Linearisierung allerdings nicht bei allen Sensoren. | ||
| + | |||
| + | * Man überlässt die Linearisierung den mathematischen Fähigkeiten eines Prozessors, z.B. einem ATMega-x, an dessen ADC der PTC angeschlossen ist. Das Verfahren ist sehr universell, benötigt aber einiges an Programmcode. | ||
| + | |||
| + | ==Schaltungsbeispiele== | ||
| + | |||
| + | === Brückenschaltung === | ||
| + | [[Bild:PT1000-Brücke.png]] | ||
| + | |||
| + | Eine einfache, aber dennoch gute Auswerteschaltung ist eine Brückenschaltung. Wegen der relativ kleinen Spannungsänderungen wird oft eine Verstärkung benötigt, vor allem beim <b>Pt100</b> oder — Strom sparender — <b>Pt1000</b>. | ||
| + | Bei den gezeigten Widerstandswerten reicht der Messbereich von etwa -25 °C bis +250 °C für 0 bis V+ (z.B. 5 V) am Ausgang. Über die Widerstände R2 und R3 kann der Bereich angepasst werden. Mit R3 = 20 kΩ hätte man z.B. einen Messbereich von etwa -10 °C bis + 130 °C. Die Linearisierung erfolgt in der Regel digital hinter dem A/D-Wandler. Die Referenzspannung des A/D-Wandlers sollte V+ sein, für eine ratiometrische Messung. Wenn nur eine Versorgung (z.B. 5 V) zur Verfügung stehen, sollte V+ an den Ausgangsbereich des OPs angepasst sein, also etwa 3 V für den LM358 (oder den besseren LT1013), oder der Operationsverstärker eine Rail-to-Rail-Typ (z.B. MCP6001) sein, wenn der AD mit der Versorgungsspannung als Ref. Arbeitet. | ||
| + | |||
| + | {{Ausbauwunsch|... auf jeden Fall Anwendungs- und Schaltungsbeispiele mit Heiß- oder Kaltleiter!'''}} | ||
| + | |||
| + | === Spannungsteiler === | ||
| + | |||
| + | Für <b>NTC</b> (Heißleiter) bietet sich ein einfacher Spannungsteiler an. Den Vorwiderstand dimensioniert man so, dass er etwa so groß ist wie der Widerstandswert <i>in der Mitte des gewünschten Temperatur-Messbereiches</i>. Die A/D-Wandlung erfolgt „ratiometrisch“ mit dem vollen Speisespannungsbereich. Dann hat man — nach der Linearisierung in Software — etwas oberhalb der Mitte (zu niedrigeren Temperaturen hin) die höchste und am den beiden Rändern gleichmäßig abnehmende Auflösung. Von Vorteil bei dieser Lösung ist, dass man sich über den Messbereich keine Gedanken machen muss, er ist prinzipiell 0 K .. ∞ K, und die Auflösung nimmt zu den beiden Extrema kontinuierlich ab. | ||
| + | |||
| + | ==== Rechenbeispiel (NTC mit 220 kΩ bei 25 °C) ==== | ||
| + | <table border cellspacing=0 cellpadding=4> | ||
| + | <tr bgcolor=#FFFFE0><th>Temperatur<th>NTC-Widerstandswert<th>Vorwiderstand<th>Ausgangsspannung<th>Auflösung | ||
| + | <tr><td>0 °C<td>844 kΩ<td rowspan=6>100 kΩ<td>U<sub>B</sub> * 0,894<td rowspan=2>10 bit: 0,4 K<br>12 bit: 0,1 K | ||
| + | <tr><td>10 °C<td>500 kΩ<td>U<sub>B</sub> * 0,667 | ||
| + | <tr bgcolor=#E0FFE0><td>40 °C<td>120 kΩ<td>U<sub>B</sub> * 0,545<td rowspan=2>10 bit: 0,1 K<br>12 bit: 0,025 K | ||
| + | <tr bgcolor=#E0FFE0><td>50 °C<td>80 kΩ<td>U<sub>B</sub> * 0,444 | ||
| + | <tr><td>130 °C<td>5,63 kΩ<td>U<sub>B</sub> * 0,053<td rowspan=2>10 bit: 0,75 K<br>12 bit: 0,2 K | ||
| + | <tr><td>140 °C<td>4,21 kΩ<td>U<sub>B</sub> * 0,040 | ||
| + | </table> | ||
| + | |||
| + | ==== Grafisches Rechenbeispiel mittels WolframAlpha ==== | ||
| + | * [http://www.wolframalpha.com/input/?i=log+plot+y=220000*exp(4000*(1/(275%2Bx)-1/300)),+x=-50+to+150 Kennlinie (R über T)], die Exponentialkonstante '''B''' ist hier gleich 4000 angesetzt. | ||
| + | * [http://www.wolframalpha.com/input/?i=plot+y=1/(1%2B1/exp(4000*(1/(275%2Bx)-1/300))),+x=-50+to+150 Ausgangsspannung (U/U<sub>B</sub> über T)], der Heißleiter befindet sich einpolig auf Masse, daher nimmt die Spannung mit steigender Temperatur ab. Der Vorwiderstand ist hier genauso groß wie der Heißleiter-Widerstand bei 25 °C (Nennwiderstand). Am Wendepunkt der s-förmigen Kurve ist die Steilheit und damit die Auflösung am größten. | ||
| + | * [http://www.wolframalpha.com/input/?i=plot+derive+y=1/(1%2B1/exp(4000*(1/(275%2Bx)-1/300))),+x=-50+to+150 Steilheit (<i>d</i>U/U<sub>B</sub> über T) = Ableitung], der Wert -0,01 bedeutet ≈ 0,1 K Auflösung bei 1024 A/D-Werten (eines 10-bit-A/D-Wandlers). | ||
| + | |||
| + | ==== Tipp zur Spreizung des Messbereichs ==== | ||
| + | |||
| + | Möchte man den ''genau arbeitenden'' Messbereich vergrößern, ist es am einfachsten, den Vorwiderstand ''umschaltbar'' zu machen! | ||
| + | |||
| + | Ein per Portpin schaltbarer Widerstand ist ohnehin nötig, wenn die Widerstandsmessung bei einem batteriebetriebenen Aufnehmer nur kurzzeitig erfolgen soll. Um Querstrom zu vermeiden, ist für die jeweiligen niederohmigen Widerstände (sofern umschaltbar mehrere vorhanden) an einem Pin anzuschließen, dessen digitaler Einang abtrennbar ist. Bei manchen Controllern, etwa MSP430x2xx, ist man da eingeschränkt. | ||
| + | |||
| + | Da beide A/D-Wandlungen ratiometrisch arbeiten, sind keinerlei Referenzspannungen erforderlich. Die Maßverkörperung (Vergleichsnormal) erfolgt mit dem Festwiderstand bzw. den Festwiderständen. | ||
| + | |||
| + | === Mehr Auflösung === | ||
| + | |||
| + | <i>… bedeutet nicht unbedingt mehr Genauigkeit!</i> | ||
| + | |||
| + | Hier gibt es prinzipiell drei Wege: | ||
| + | * Einschränken des Wandlungsbereiches durch Brückenschaltung und Verstärkung : Geringerer Messumfang<br><i>Typische Anwendung: Fieberthermometer</i> | ||
| + | * Verwenden eines besseren (externen) A/D-Wandlers - kann sich angesichts der gesunkenen Preise mittlerweile lohnen. | ||
| + | * Verwenden eines anderen Wandlungsprinzips in Mikrocontroller-Software. In der einfachsten Form Oversampling (d.h. häufiges abtasten und Mitteln) mit dem vorhandenen ADC im µC. Möglich, wenn auch nicht besonders genau, ist etwa ein Einflanken-Umsetzer mit dem µC internen Analog-Komparator,der wenig externe Beschaltung erfordert. | ||
==Siehe auch== | ==Siehe auch== | ||
| Zeile 38: | Zeile 133: | ||
==Weblinks== | ==Weblinks== | ||
| − | [http://de.wikipedia.org/ Wikipedia] | + | [http://de.wikipedia.org/wiki/Kaltleiter Wikipedia: Kaltleiter] |
| + | |||
| + | [http://www.maxim-ic.com/app-notes/index.mvp/id/3450 Schaltung für PT100 mit Linearisierung] | ||
| − | + | [[Kategorie:Elektronik]] | |
| − | + | [[Kategorie:Sensoren]] | |
Aktuelle Version vom 20. Februar 2015, 22:08 Uhr
Heißleiter (engl. NTC, negative temperature coefficient) und Kaltleiter (engl. PTC, positive temperature coefficient) sind elektrische Widerstände aus bestimmten Materialien, deren Leitfähigkeit (und damit der Widerstand) sich mit der Temperatur deutlich ändert.
Inhaltsverzeichnis
NTCs
Heißleiter sind stromleitende Materialien, die bei hohen Temperaturen eine höhere Leitfähigkeit besitzen als bei tiefen Temperaturen. Sie haben einen negativen Temperaturkoeffizienten; das heißt, mit steigender Temperatur sinkt ihr elektrischer Widerstand.Ein großer Vorteil ist die starke Temperaturabhängigkeit und der geringe Preis. Das nichtlineare Verhalten des Widerstandswertes bei sich verändernder Temperatur ist jedoch zugleich auch der größte Nachteil.
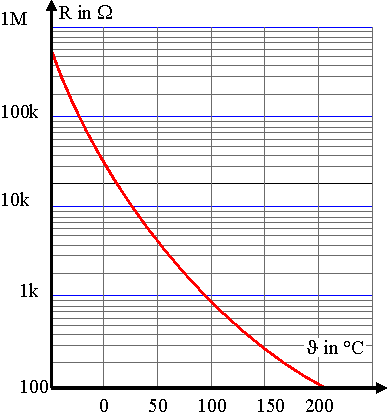
Ein einzelner, nicht kompensierter NTC ändert seinen Widerstand nicht linear. Hier dazu ein Beispieldiagramm:
Temperaturabhängigkeit
Mithilfe eines NTCs lässt sich ein einfacher Temperatursensor bauen.
Bildet der Heißleiter einen Spannungsteiler mit einem konstanten Widerstand, so lässt sich die geteilte Spannung mithilfe eines Microcontrollers messen, wodurch auf den Widerstand des NTCs geschlossen werden kann.
Der Heißleiter ändert seinen elektrischen Widerstand nicht linear. Jedoch kann die Temperatur auch rechnerisch ermittelt werden. Es gilt:
T ~ 1/ln(R)
Bei Einbeziehung der Aktivierungsenergie, der Nenntemperatur (meist 25°C), und des Nennwiderstandes bei Nenntemperatur
gilt folgende Funktion:
T(R) = T_N * B / (B + T_N * ln(R / R_N))
Wobei T die momentane Temperatur, T_N die Nenntemperatur (in Kelvin), R der Widerstand des Heißleiters und R_N den Nennwiderstand darstellt. Bei B handelt es sich um eine Materialkonstante, die vom Herrsteller im Datenblatt angegeben wird. Bei Implementierung der Funktion in ein Programm für den Microcontroller müssen umbedingt die Datentypen berücksichtigt werden!
| Dieser Artikel ist noch lange nicht vollständig. Der Auto/Initiator hofft das sich weitere User am Ausbau des Artikels beteiligen.
Das Ergänzen ist also ausdrücklich gewünscht! Besonders folgende Dinge würden noch fehlen: Erbitte Implementierung der Gleichungen (Unbekannter Parserfehler) |
PTCs
Kaltleiter sind stromleitende Materialien, die bei hohen Temperaturen eine niedrigere Leitfähigkeit besitzen als bei tiefen Temperaturen. Sie haben einen positiven Temperaturkoeffizienten; das heißt, mit steigender Temperatur steigt auch ihr elektrischer Widerstand.
Bei den PTCs gibt es zwei Sorten: Einmal welche mit näherungsweise linearer Kennlinie und dann welche mit stark nichtlinearer Kennlinie. Die linearen Typen (z.B. KTYxx Reihe) oder Platinwiderstände (z.B. PT100, PT1000 ) sind mehr für die Temperaturmessung gedacht. Recht beliebt sind die PTCs der KTYxx-Reihe z.B. der KTY81-110. Sie sind sehr günstig (ca. 0,50€) und bieten für die meisten Anwendungen eine ausreichende Genauigkeit.
Für höhere Anforderungen an den Messbereich (je nach Typ von -260 ... 850 °C) oder die Genauigkeit gibt es Platin-Widerstände zur Temperaturmessung. Auch hier ist der Temperaturkoeffizient positiv (0,38 %/K bei Raumtemperatur). Am häufigsten findet man hier Widerstände von 100 Ohm (PT100) und 1000 Ohm (PT1000). Diese sind jedoch relativ teurer (je nach Typ und Bezugsquelle und Qualität ab etwa 3 €).
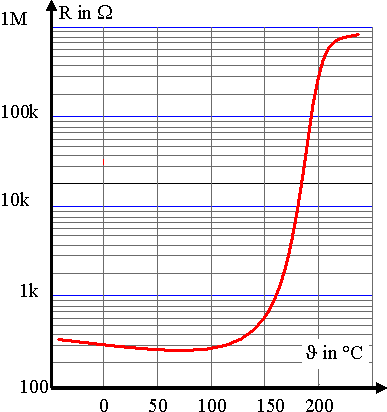
Die stark nichtlinearen Typen sind mehr als Übertemperaturschutz oder als selbst rückstellende Sicherung geeignet. Auch dazu ein Beispieldiagramm für einen nicht linearen PTC:
Einatzmöglichkeiten
Mit NTCs und PTCs lassen sich in "normalen" Bereichen (das heißt hier kleiner etwa 200 °C) günstig Temperaturen messen. Dieses Gebiet umfasst alles vom kleinen digitalen Fieberthermometer über die verschiedenen Anzeigeinstrumente (wie Wetterstationen und KFZ-Elektronik) bis hin zu kompletten Heizungs- und Klimasteuerungen in Gebäuden.
Daneben gibt es auch Anwendungen bei denen es nicht um eine eigentliche Messung geht:
- spezielle NTCs werden z.B. bei Netzteilen als Einschaltstrombegrenzer genutzt. Hier wird die Eigenerwärmung als gewollter Effekt genutzt: die Bauteile sind im kalten Zustand so hochohmig, dass beispielsweise große Elkos geladen werden, ohne dass die vorgeschaltete Sicherung auslöst. Fließt dann der Nennstrom, erwärmen sich die Bauteile und verringern ihren Widerstand. Um wieder strombegrenzend wirksam zu sein, müssen sie nach Abschalten des Gerätes erst abkühlen.
- PTC-Sicherungen schalten den Strom aufgrund ihrer Eigenerwärmung bei Überlastung ab. Sie sind gut für Verbraucher geeignet, die kurzzeitig Überlast vertragen (z.B. Transformatoren), da die Auslösung relativ träge ist. Erst nach Trennen der Stromversorgung stellen sich die PTC-Sicherungen durch Abkühlung zurück. Bei der Auswahl von PTC-Sicherungen muss neben Halte- und Abschaltstrom deren Maximalstrom und die Maximalspannung beachtet werden.
- PTC-Heizelemente können selbst ihre Temperatur regeln. Sie ist werkstoffabhängig.
Temperaturmessung mit PTC
Um aus der Widerstandsänderung am Sensor eine passende Spannung zu erzeugen gibt es verschieden Möglichkeiten. Ein naheliegender Weg ist eine Konstantstromquelle, so dass die Spannung am Sensor direkt proportional zum Widerstand ist. Wenn man das Signal danach digitalisieren will, hat dieser Weg aber zwei wesentliche Nachteile: Eine gute Konstantstromquelle ist aufwendig, und man hat dann 2 Referenzen im System und damit unnötige Fehlerquellen. Für eine Widerstandsmessung ist ein Widerstand als Vergleichswert besser und einfacher als das Verhältnis von einer Spannungsquelle und einer Stromquelle. Dafür gibt es im wesentlichen 3 Möglichkeiten:
1) Der selbe Strom fließt durch den Sensor und den Vergleichswiderstand. Die Spannung an Vergleichswiderstand wird als Referenz für den AD Wandler benutzt, die Spannung am Sensor wird gemessen. Dieses Verfahren ist vor allem mit hochauflösenden AD Wandlern mit Differenzeingängen (z.B. LTC2440) sinnvoll.
2) Der selbe AD Wandler misst nacheinander die Spannung am Sensor und Vergleichswiderstand. Dafür braucht man 2 Eingänge mit Differenzeingang.
3) Der Sensor und der Vergleichswiderstand bilden einen Spannungsteiler. Die Spannung über den Spannungsteiler dient als Referenz für den AD-wandler. Anders als bei den beiden vorherigen Möglichkeiten ist das Ergebnis der AD Wandlung hier nicht mehr linear vom Widerstand abhängig. Bei einem kleinen Messbereich und geringer Auflösung des AD's lohnt es sich ggf. den konstanten Teil der Spannung abzuziehen, damit der Wertebereich des AD Wandler weitgehend ausgenutzt werden kann. Die Schaltung ist dann eine Brückenschaltung.
In allen 3 Fällen muss der Strom nicht besonders stabilisiert sein und es wird keine stabile Referenzspannung für den AD benötigt. Es kommt nur auf das Spannungsverhältnis an.
Beim Strom durch den Sensor muss ein Kompromiss zwischen genügend Spannung und der Eigenerwärmung des Sensors gefunden werden. Bei mehr als etwa 1 mW Verlustleistung am Sensor wird eine genaue Temperaturmessung schwierig. Für genaue Messungen mit dem PT100 werden oft sogar 0,1 mW als Grenze angegeben, d.h der Strom liegt bei nur 1 mA.
Linearisierung
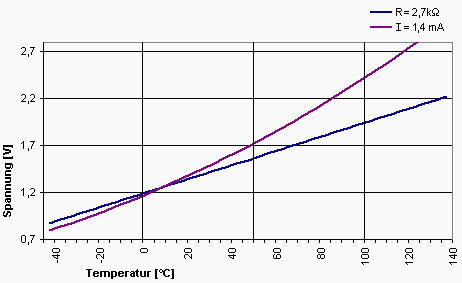
Um trotz der nicht linearen Kennlinie des Sensors ein linear von der Messgröße (Temperatur) abhängiges Ergebnis (Spannung oder Digitaler Wert) zu erhalten, bieten sich verschiedene Methoden an:
- Man nutzt die Nichtlineare Kennlinie von Dioden. Wegen der Temperaturabhängigkeit der Diodenkennlinie ist das aber schwierig und nur für sehr starke Nichtlinearitäten gerechtfertigt. Für die schwache Nichtlinearität der PTCs ist das Verfahren eher ungeeignet.
- Man nutzt den nichtlinearen Zusammenhang zwischen Spannung und Widerstand beim Spannungsteiler, bzw. in einer Brückenschaltung. Bei den Sensoren des Typs KTY81 wird mit einem 2,7kOhm-Widerstand in Reihe gerade eine relativ gute Kompensation der Nichtlinearitäten erreicht. Im Bereich von -40 °C ... +140 °C erscheint der PTC nun nahezu linear, der verbleibende Linearitätsfehler liegt bei etwa ±10 mV (für 5 V am Spannungsteiler). So einfach geht die Linearisierung allerdings nicht bei allen Sensoren.
- Man überlässt die Linearisierung den mathematischen Fähigkeiten eines Prozessors, z.B. einem ATMega-x, an dessen ADC der PTC angeschlossen ist. Das Verfahren ist sehr universell, benötigt aber einiges an Programmcode.
Schaltungsbeispiele
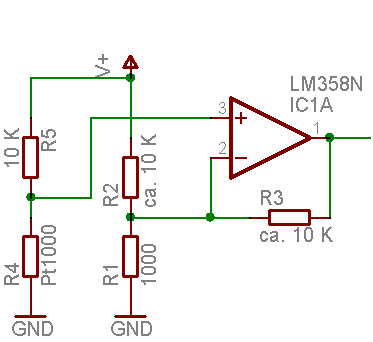
Brückenschaltung
Eine einfache, aber dennoch gute Auswerteschaltung ist eine Brückenschaltung. Wegen der relativ kleinen Spannungsänderungen wird oft eine Verstärkung benötigt, vor allem beim Pt100 oder — Strom sparender — Pt1000. Bei den gezeigten Widerstandswerten reicht der Messbereich von etwa -25 °C bis +250 °C für 0 bis V+ (z.B. 5 V) am Ausgang. Über die Widerstände R2 und R3 kann der Bereich angepasst werden. Mit R3 = 20 kΩ hätte man z.B. einen Messbereich von etwa -10 °C bis + 130 °C. Die Linearisierung erfolgt in der Regel digital hinter dem A/D-Wandler. Die Referenzspannung des A/D-Wandlers sollte V+ sein, für eine ratiometrische Messung. Wenn nur eine Versorgung (z.B. 5 V) zur Verfügung stehen, sollte V+ an den Ausgangsbereich des OPs angepasst sein, also etwa 3 V für den LM358 (oder den besseren LT1013), oder der Operationsverstärker eine Rail-to-Rail-Typ (z.B. MCP6001) sein, wenn der AD mit der Versorgungsspannung als Ref. Arbeitet.
| Dieser Artikel ist noch lange nicht vollständig. Der Auto/Initiator hofft das sich weitere User am Ausbau des Artikels beteiligen.
Das Ergänzen ist also ausdrücklich gewünscht! Besonders folgende Dinge würden noch fehlen: ... auf jeden Fall Anwendungs- und Schaltungsbeispiele mit Heiß- oder Kaltleiter! |
Spannungsteiler
Für NTC (Heißleiter) bietet sich ein einfacher Spannungsteiler an. Den Vorwiderstand dimensioniert man so, dass er etwa so groß ist wie der Widerstandswert in der Mitte des gewünschten Temperatur-Messbereiches. Die A/D-Wandlung erfolgt „ratiometrisch“ mit dem vollen Speisespannungsbereich. Dann hat man — nach der Linearisierung in Software — etwas oberhalb der Mitte (zu niedrigeren Temperaturen hin) die höchste und am den beiden Rändern gleichmäßig abnehmende Auflösung. Von Vorteil bei dieser Lösung ist, dass man sich über den Messbereich keine Gedanken machen muss, er ist prinzipiell 0 K .. ∞ K, und die Auflösung nimmt zu den beiden Extrema kontinuierlich ab.
Rechenbeispiel (NTC mit 220 kΩ bei 25 °C)
| Temperatur | NTC-Widerstandswert | Vorwiderstand | Ausgangsspannung | Auflösung |
|---|---|---|---|---|
| 0 °C | 844 kΩ | 100 kΩ | UB * 0,894 | 10 bit: 0,4 K 12 bit: 0,1 K |
| 10 °C | 500 kΩ | UB * 0,667 | ||
| 40 °C | 120 kΩ | UB * 0,545 | 10 bit: 0,1 K 12 bit: 0,025 K | |
| 50 °C | 80 kΩ | UB * 0,444 | ||
| 130 °C | 5,63 kΩ | UB * 0,053 | 10 bit: 0,75 K 12 bit: 0,2 K | |
| 140 °C | 4,21 kΩ | UB * 0,040 |
Grafisches Rechenbeispiel mittels WolframAlpha
- Kennlinie (R über T), die Exponentialkonstante B ist hier gleich 4000 angesetzt.
- Ausgangsspannung (U/UB über T), der Heißleiter befindet sich einpolig auf Masse, daher nimmt die Spannung mit steigender Temperatur ab. Der Vorwiderstand ist hier genauso groß wie der Heißleiter-Widerstand bei 25 °C (Nennwiderstand). Am Wendepunkt der s-förmigen Kurve ist die Steilheit und damit die Auflösung am größten.
- Steilheit (dU/UB über T) = Ableitung, der Wert -0,01 bedeutet ≈ 0,1 K Auflösung bei 1024 A/D-Werten (eines 10-bit-A/D-Wandlers).
Tipp zur Spreizung des Messbereichs
Möchte man den genau arbeitenden Messbereich vergrößern, ist es am einfachsten, den Vorwiderstand umschaltbar zu machen!
Ein per Portpin schaltbarer Widerstand ist ohnehin nötig, wenn die Widerstandsmessung bei einem batteriebetriebenen Aufnehmer nur kurzzeitig erfolgen soll. Um Querstrom zu vermeiden, ist für die jeweiligen niederohmigen Widerstände (sofern umschaltbar mehrere vorhanden) an einem Pin anzuschließen, dessen digitaler Einang abtrennbar ist. Bei manchen Controllern, etwa MSP430x2xx, ist man da eingeschränkt.
Da beide A/D-Wandlungen ratiometrisch arbeiten, sind keinerlei Referenzspannungen erforderlich. Die Maßverkörperung (Vergleichsnormal) erfolgt mit dem Festwiderstand bzw. den Festwiderständen.
Mehr Auflösung
… bedeutet nicht unbedingt mehr Genauigkeit!
Hier gibt es prinzipiell drei Wege:
- Einschränken des Wandlungsbereiches durch Brückenschaltung und Verstärkung : Geringerer Messumfang
Typische Anwendung: Fieberthermometer - Verwenden eines besseren (externen) A/D-Wandlers - kann sich angesichts der gesunkenen Preise mittlerweile lohnen.
- Verwenden eines anderen Wandlungsprinzips in Mikrocontroller-Software. In der einfachsten Form Oversampling (d.h. häufiges abtasten und Mitteln) mit dem vorhandenen ADC im µC. Möglich, wenn auch nicht besonders genau, ist etwa ein Einflanken-Umsetzer mit dem µC internen Analog-Komparator,der wenig externe Beschaltung erfordert.
Siehe auch
Weblinks