(→Temperaturmessung mit PTC) |
(→Linearisierung) |
||
| Zeile 51: | Zeile 51: | ||
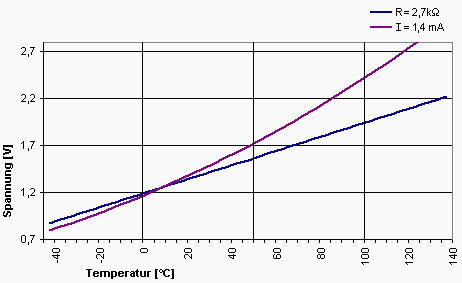
KTY81 mit konstanten Strom (1,4 mA), und mit Widerstand in Reihe. | KTY81 mit konstanten Strom (1,4 mA), und mit Widerstand in Reihe. | ||
| − | + | Um trotz der nicht linearen Kennline des Sensors ein linear von der Messgröße (Temperatur) abhängiges Ergebnis (Spannung oder Digitaler Wert) zu erhalten, bieten sich verschiedene Methoden an: | |
| − | + | ||
* Man nutzt die Nichtlineare Kennline von Dioden. Wegen der Temperaturabhängigkeit der Diodenkennline ist das aber schwierig und nur für sehr strarke nichtlinearitäten gerechtfertigt. Für die schwache nichtlinearität der PTCs ist das Verfahren eher ungeeignet. | * Man nutzt die Nichtlineare Kennline von Dioden. Wegen der Temperaturabhängigkeit der Diodenkennline ist das aber schwierig und nur für sehr strarke nichtlinearitäten gerechtfertigt. Für die schwache nichtlinearität der PTCs ist das Verfahren eher ungeeignet. | ||
| − | * Man nutzt den nichtlinearen Zusammenhang zwischen Spannung und Widerstand bei beim Spannungsteiler, bzw. in einer Brückenschaltung. Bei den Sensoren des Typs KTY81 wird mit einem 2,7kOhm-Widerstand in Reihe gerade eine relativ gute Kompensation der nichtlinearitäten erreicht. Im Bereich von -40 °C ... +140 °C erscheint der PTC nun nahezu linear, der verbleibende Linearitätsfehler liegt bei etwa ±10 mV (für 5 V am Spannungsteiler) | + | * Man nutzt den nichtlinearen Zusammenhang zwischen Spannung und Widerstand bei beim Spannungsteiler, bzw. in einer Brückenschaltung. Bei den Sensoren des Typs KTY81 wird mit einem 2,7kOhm-Widerstand in Reihe gerade eine relativ gute Kompensation der nichtlinearitäten erreicht. Im Bereich von -40 °C ... +140 °C erscheint der PTC nun nahezu linear, der verbleibende Linearitätsfehler liegt bei etwa ±10 mV (für 5 V am Spannungsteiler). So einfach geht die Linearisierung allerdings nicht bei allen Sensoren. |
| − | * Man überläßt die Linearisierung den mathematischen Fähigkeiten eines Prozessors, z.B. einem ATMega-x, an dessen ADC der PTC angeschlossen ist. Das Verfahren ist sehr universell, benötigt aber einiges an Programmcode | + | * Man überläßt die Linearisierung den mathematischen Fähigkeiten eines Prozessors, z.B. einem ATMega-x, an dessen ADC der PTC angeschlossen ist. Das Verfahren ist sehr universell, benötigt aber einiges an Programmcode. |
| − | + | ||
| − | + | ||
| − | + | ||
==Schaltungsbeispiele== | ==Schaltungsbeispiele== | ||
Version vom 1. Juni 2010, 20:59 Uhr
Heißleiter (engl. NTC, negative temperature coefficient) und Kaltleiter (engl. PTC, positive temperature coefficient) sind elektrische Widerstände aus bestimmten Materialien, deren Leitfähigkeit (und damit der Widerstand) sich mit der Temperatur deutlich ändert.
Inhaltsverzeichnis
NTCs
Heißleiter sind stromleitende Materialien, die bei hohen Temperaturen eine höhere Leitfähigkeit besitzen als bei tiefen Temperaturen. Sie haben einen negativen Temperaturkoeffizienten; das heißt, mit steigender Temperatur sinkt ihr elektrischer Widerstand.Ein großer Vorteil ist die starke Temperaturabhängigkeit und der geringe Preis. Das nichtlineare Verhalten des Widerstandswertes bei sich verändernder Temperatur ist jedoch zugleich auch der größte Nachteil.
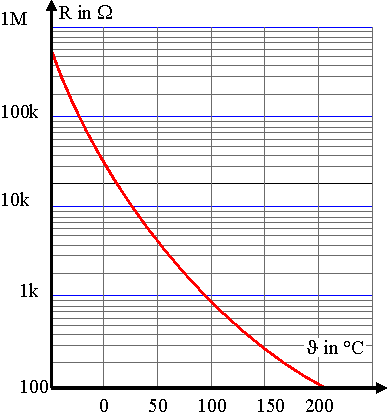
Ein einzelner, nicht kompensierter NTC ändert seinen Widerstand nicht linear. Hier dazu ein Beispieldiagramm:
PTCs
Kaltleiter sind stromleitende Materialien, die bei hohen Temperaturen eine niedrigere Leitfähigkeit besitzen als bei tiefen Temperaturen. Sie haben einen positiven Temperaturkoeffizienten; das heißt, mit steigender Temperatur steigt auch ihr elektrischer Widerstand.
Bei den PTCs gibt es zwei Sorten: Einmal welche mit näherungsweise linearer Kennlinie und dann welche mit stark nichtlinearer Kennlinie. Die linearen Typen (z.B. KTYxx Reihe) oder Platinwiderstände (z.B. PT100, PT1000 ) sind mehr für die Temperaturmessung gedacht. Recht beliebt sind die PTCs der KTYxx-Reihe z.B. der KTY81-110. Sie sind sehr günstig (ca. 0,50€) und bieten für die meisten Anwendungen eine ausreichende Genauigkeit.
Im Vergleich zu anderen PTCs oder NTCs ist bei den PTxxx-Typen im Bereich von -200...500 °C die Kennlinie nahezu linear steigend. Dafür ist der Temperaturkoeffizient deutlich kleiner (0,38 %/K bei Raumtemperatur). Es gibt diese Kaltleiter in den Serien PT100 (mit 100 Ohm Innenwiderstand) oder PT1000 (mit 1000 Ohm). Diese sind jedoch erheblich teurer (je nach Typ und Bezugsquelle und Qualität ab etwa 3 €) als die anderen Typenreihen und werden eingesetzt, wenn höhere Anforderungen an Messbereich oder Genauigkeit gestellt werden.
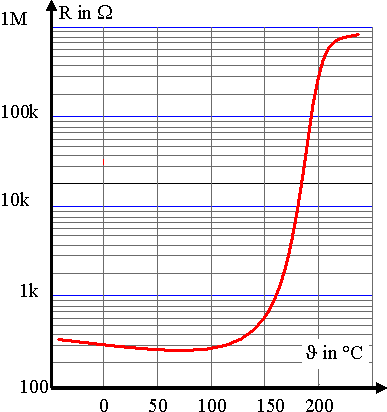
Die stark nichtlinearen Typen sind mehr als Übertemperaturschutz oder als selbst rückstellende Sicherung geeignet. Auch dazu ein Beispieldiagramm für einen nicht linearen PTC:
Einatzmöglichkeiten
NTCs und PTCs werden immer dann eingesetzt, wenn in "normalen" Bereichen (das heißt hier kleiner etwa 200 °C) eine Temperatur gemessen werden soll. Dieses Gebiet umfasst alles vom kleinen digitalen Fieberthermometer über die verschiedenen Anzeigeinstrumente (wie Wetterstationen und KFZ-Elektronik) bis hin zu kompletten Heizungs- und Klimasteuerungen in Gebäuden.
Für Temperaturen größer etwa 150 °C werden meist spezielle Sensoren eingesetzt, wie z.B. Thermoelemente oder Platinwiderstände.
Temperaturmessung mit PTC
Um aus der Widerstandsänderung am Sensor eine passende Spannung zu erzeugen gibt es verschieden Möglichkeiten. Ein naheliegender Weg ist eine Konstantstromquelle, so dass die Spannung am Sensor direkt proportional zum Widerstand ist. Wenn man das Signal danach digitalisieren will, hat dieser Weg aber zwei wesenliche Nachteile: Eine gute Konstantstromquelle ist aufwendig, und man hat dann 2 Referenzen im System und damit unnötige Fehlerquellen. Für eine Widerstandsmessung ist ein Widerstand als Vergleichswert besser und einfacher als das Verhältnis von einer Spannungquelle und einer Stromquelle. Dafür gibt es im wesentlichen 3 Möglichkeiten:
1) Der selbe Strom fleißt durch den Sensor und den Vergleichwiderstand. Die Spannung an Vergleichswiderstand wird als Referenz für den AD Wandler benutz, die Spannung am Sensor wird gemessen.
2) Der selbe AD Wandler mißt nacheinander die Spannung am Sensor und Vergleichswiderstand.
3) Der Sensor und der Vergleichswiderstand bilden einen Spannunsgteiler. Die Spannung über den Spannungsteiler dient als Referenz für den AD-wandler. Anders als bei den beiden vorherigen Möglichkeiten ist das Ergebnis der AD Wandlung hier nicht mehr linear vom Widerstand abhängig.
In allen 3 Fällen muß der Strom nicht besonders stabilisiert sein, und es geht ohne stabile Referenzspannung für den AD. Es kommt nur auf das Spannungsverhältnis an.
Bei einem kleinen Messbereich lohnt es sich den konstanten Teil der Spannung abzuziehen, damit der Wertebereich des AD Wandler weitgehend ausgenutzt werden kann. Beim Strom durch den Sensor muß ein Kompromiss zwischen genügend Spannung und dem Stromverbauch und der damit verbundenen Eigenerwärmung des Sensors gefunden werden. Bei mehr als etwa 1 mW Verlustleistung am Sensor wird eine genaue Temperaturmessung schwierig.
Linearisierung
Um trotz der nicht linearen Kennline des Sensors ein linear von der Messgröße (Temperatur) abhängiges Ergebnis (Spannung oder Digitaler Wert) zu erhalten, bieten sich verschiedene Methoden an:
- Man nutzt die Nichtlineare Kennline von Dioden. Wegen der Temperaturabhängigkeit der Diodenkennline ist das aber schwierig und nur für sehr strarke nichtlinearitäten gerechtfertigt. Für die schwache nichtlinearität der PTCs ist das Verfahren eher ungeeignet.
- Man nutzt den nichtlinearen Zusammenhang zwischen Spannung und Widerstand bei beim Spannungsteiler, bzw. in einer Brückenschaltung. Bei den Sensoren des Typs KTY81 wird mit einem 2,7kOhm-Widerstand in Reihe gerade eine relativ gute Kompensation der nichtlinearitäten erreicht. Im Bereich von -40 °C ... +140 °C erscheint der PTC nun nahezu linear, der verbleibende Linearitätsfehler liegt bei etwa ±10 mV (für 5 V am Spannungsteiler). So einfach geht die Linearisierung allerdings nicht bei allen Sensoren.
- Man überläßt die Linearisierung den mathematischen Fähigkeiten eines Prozessors, z.B. einem ATMega-x, an dessen ADC der PTC angeschlossen ist. Das Verfahren ist sehr universell, benötigt aber einiges an Programmcode.
Schaltungsbeispiele
| Dieser Artikel ist noch lange nicht vollständig. Der Auto/Initiator hofft das sich weitere User am Ausbau des Artikels beteiligen.
Das Ergänzen ist also ausdrücklich gewünscht! Besonders folgende Dinge würden noch fehlen: ... auf jeden Fall Anwendungs- und Schaltungsbeispiele mit Heiß- oder Kaltleiter! |
Siehe auch
Weblinks