Aus RN-Wissen.de
Wechseln zu: Navigation, Suche
LiFePO4 Speicher Test

Zeile 307: Zeile 307:
 
:- bei flachen Öffnungswinkeln flachere Verrundungen als Kurve 1),  
 
:- bei flachen Öffnungswinkeln flachere Verrundungen als Kurve 1),  
 
:- bei spitzeren Öffnungswinkeln spitzere Verrundungen als Kurve 1).  
 
:- bei spitzeren Öffnungswinkeln spitzere Verrundungen als Kurve 1).  
−
 
−
 
 
* Liegen die Tangenten der zu verbindenden Segmente parallel, so erzeugt Kurve 1) einen Halbkreis, Kurve 2) eine Halb-Ellipse.
 
* Liegen die Tangenten der zu verbindenden Segmente parallel, so erzeugt Kurve 1) einen Halbkreis, Kurve 2) eine Halb-Ellipse.
 
* Kurve 3) "reagiert stärker" auf Änderungen des Öffnungswinkels und der Schnittpunktlage als die beiden anderen; dies kann in sehr "elegante" aber auch völlig unbrauchbare Kurven führen.  
 
* Kurve 3) "reagiert stärker" auf Änderungen des Öffnungswinkels und der Schnittpunktlage als die beiden anderen; dies kann in sehr "elegante" aber auch völlig unbrauchbare Kurven führen.  

Version vom 5. Juni 2016, 19:33 Uhr

Vorwort

Irgendwie hatte sich aus Diskussionen zur Knickarm-Robotermechanik die Frage ergeben, …"und wie berechnen Sie das?" Meine Antwort war, "Mit EXCEL® ist das recht einfach. Ganz so einfach war es dann doch nicht. Im Internet findet sich zwar einiges zum Thema, aber wenig Problem orientiertes im Focus Robotic. Meine Recherchen führten mich so zunächst in die Entwicklung Robotic orientierter Algorithmen.

  • Hier, im Teil 2 finden Sie Praxis orientierte Problemlösungen. Besprochen werden ein 3D Bahngenerator und die aus der "Sollbahn" berechneten Winkel der Knickarme.
Hierzu sollten Sie die kostenlose Test und Demo-Version downloaden.
  • Teil 1 dieses Artikels Inverse Kinematik 1 – Theorie (Tutorial) gibt theoretischen Back-Ground. Hier finden Sie Hintergrundinformation zu Problemen der Kinematik, theoretische Lösungsansätze und die Mathematik der Winkeltransformation. Für die Nutzung des Gelenkbaukastens ist es nicht unbedingt erforderlich, dieses zu lesen – es kann aber hilfreich sein!


Mathematischer 3D Gelenk-Baukasten

Dieser Artikel ist ein (weitestgehnd) produkt-neutraler Handbuch–Auszug; er orientiert sich jedoch an der auf EXCEL®-Basis realisierten Problemlösung.

Systemüberblick

Der Baukasten ist aus der Aufgabe entstanden, anwenderorientiert und Hardware neutral

  • Rotations- und Teleskopachsen für Knickarm-Robotersysteme beliebiger Bauart & Geometrie - ggf. auf Portal verfahrbar - mathematisch zusammenzustellen, um deren Bewegungsbahn 3D zu simulieren,
  • eine gegebene Hardware hierzu produktspezifisch zu parametrieren
  • oder durch Auswahl geeigneter Hardware Komponenten ein optimales Gesamtsystem zu konfigurieren.
  • Gelenk-Winkel und XYZ-Koordinaten wahlweise direkt oder invers zu berechnen und
  • das Roboter-System im 3D-Raum zu visualisieren.
  • In Anlehnung an die 8-Achsen Bahnsteuerung RoBo-mac's berechnet der Gelenk-Baukasten 8 Achsen mit jeweils 2 Freiheitsgraden (Teleskop-Dreh-Achse). Der Algorithmus ermöglicht beliebig viele kaskadierbare Achsen und ist somit erweiterbar.
  • Das Ergebnis steht numerisch (16-stellig / Fließkomma 15 Ziffern) zur Verfügung und wird ergänzend als 3D Grafik visualisiert.

Direkte Kinematik

Die kinematischen Grenzen werden durch Parametrierung der Achs-Längen, ihrer XYZ-Grundorientierung und der max. Achs-Drehwinkel definiert. An- und Abtrieb jedes Gelenkes kann unter beliebigem Winkel im Raum stehen. Die Werte werden über Schieber verändert und Real-Time visualisiert.

Inverse Kinematik

Um trotz Überbestimmung aus theoretisch unendlich vielen Winkel-Kombinationen möglichst geeignete Vektorlagen der Roboterarme zu berechnen verfolgt RoBo-mac mehrere, frei wählbare Bewegungsstrategien. Der Algorithmus basiert auf trigonometrischen und iterativen Elementen. Er arbeitet unabhängig von der Vorwärts Kinematik und nutzt diese für die Ergebnis-Visualisierung sowie die Positionskontrolle.

  • Die absoluten Positionierfehler Soll/Ist des TCP liegen unter 1/10.000 mm, meist in einer Größenordnung von 10-5 bis 10-6 mm.


3D-Kinematik & 2D-Perspektive

Achs-Drehwinkel und Perspektive werden über Schieber verändert und Real-Time visualisiert.

Roboter Arm 080 vollst.gif


Kartesische Koordinaten und Roboter Kinematik

Legen wir ein Blatt Papier auf den Tisch und zeichnen mit dem Bleistift ein Achsenkreuz – wir können dies auch mit einem CAD-System am Bildschirm tun – so hat der Kreuzungs-punkt per Definition die Bezeichnung "0 / 0". X- und Y-Wert sind also beide gleich "0".

Dieser Kreuzungspunkt liegt in einem willkürlichen Versatz zum Papier- bzw. Bildschirm-rand, Bildschirm bzw. Papier befinden sich in willkürlichem Abstand und Winkel zum Schreibtischrand, der Schreibtisch steht irgendwo im (Büro-) Raum usw.

  • Jeder dieser Gegenstände hat eine Bezugskante, von der üblicher Weise gemessen wird. Und, jeder dieser Gegenstände wird von einem anderen "umhaust", - er hat relative Koordinaten zu dieser Umhausung.
Eingebetet ist das System relativer Koordinaten in das Weltkoordinatensystem, auf das allerdings nur selten referenziert werden muß.

Wenn wir vor der Aufgabe stehen, daß ein Roboter gezielt irgendwo hingreifen oder eine Bewegungsbahn fahren muß, müssen wir den Zielpunkt in einem (kartesischen) Koordinaten-system erfassen auf das auch der Roboter-Fußpunkt referenziert. Während das Kartesische System achsparallel ohne Winkelwerte arbeitet sind Winkelwerte, - kaskadisch aneinander gereiht - der einzige Bezug zwischen Roboter-Fußpunkt und dem "End-Effektor"; dem Teil, das bewegt und in Position gebracht werden soll.

Drehwinkel werden in Grad gemessen – so haben wir es in der Schule gelernt! Ein Vollkreis hat 360 ° Grad – und das hat sich eingeprägt, wenngleich es andere Maß Systeme der Winkelmessung gibt: In der Geodäsie wird der Vollkreis mit 400 Gon (Neu-Grad) gemessen. Die RoBo-mac Algorithmen arbeitet intern im "Bogenmaß"; ein Vollkreis gleich "2 PI" – was nicht ganz zufällig dem Kreisumfang bei Radius = 1 entspricht!

Eine Achse kann sich beliebig oft um sich selbst drehen. 2 Umdrehungen entsprechen im (Alt-) Gradsystem einem Drehwinkel von 720°. Mathematisch ist dies unproblematisch, mechanisch ist eine Roboterachse - zumindest bei Gelenk- bzw. Knickarmrobotern - jedoch auf meist weniger als eine Vollkreisdrehung beschränkt. SCARA haben hier eine größere Freiheit. Gemeinsam ist diesen Systemen, daß nach Erreichen des maximalen Drehwinkels "zu-rückgedreht" werden muß. Robotersysteme haben somit zwischen beiden Endlagen einen Nullpunkt, der meist als symmetrisch mittig definiert wird. Sind alle Arme gestreckt, so steht das System in "Null-Stellung".

Per Definition referenziert jede Drehung eines Armes auf die Stellung des (kaskadisch vorhergehenden) Armes. Gemessen wird der Winkel zwischen den jeweils benachbarten Armen. Eigentlich beträgt der Winkel zwischen gestreckten Armen 180° (im 0° bis 360° System); da andererseits die Streckstellung aller Arme als "Null-Stellung" bezeichnet wird, macht es Sinn, den Bezugsnullpunkt in diese Position zu legen. Das Bezugssystem ist dann als +/- 180° Sy-stem definiert.

Auf unsere Aufgabe bezogen, den Roboter gezielt "irgendwo" hingreifen zu lassen, bedeutet dies, das "Irgendwo" kartesisch zu definieren und den Roboter im kartesischen System geeignet zu positionieren, den Rest übernimmt der MATHEMATISCHE 3D GELENK-BAUKASTEN


Die ersten Schritte

Wenn Sie sich in die Thematik einarbeiten, werden Sie recht schnell zu dem Schluß kommen:

  • Der Gelenkbaukasten bietet kinematische Bewegungsmöglichkeiten die zu beherrschen einige Erfahrung erfordert. Es ist wie beim Klavierspielen: Das Instrument wird vom Pianisten zum Leben erweckt! Und hier macht Übung den Meister.
Üben Sie, Sie können nichts kaputt machen, der Baukasten ist sehr bedien-tolerant. Ich habe bei der Entwicklung hohen Wert auf "Bediener-Komfort" und darauf gelegt, "Bedienungsfehler" (grausame Ausrede inkompetenter Entwickler) automatisch abzufangen. Vieles von dem was Sie tun überprüfet ein Algorithmus im Hintergrund auf Plausibilität – und meldet sich!
Stöbern Sie!

Für Ungeduldige

  • Die Datei "Demo-Arm" zeigt (nach Initialisierung der kostenlosen Test- und Demo Version) einen Bewegungsablauf. Clicken Sie in der Grafik (oben links) "Control-Center"; eine Maske erscheint; clicken Sie (Maske mitte unten) "Simulation Bewegung / vorwärts"; der Arm fährt eine Bewegungsbahn.
  • Die Datei "Demo-Arm_schief" ist Beispiel einer komplexen Inversen Kinematik mit in sich gedrehtem Arm (vgl. Tutorial).
  • Strategie-Demo
verlassen Sie das 'Control-Center'. In der 3D Grafik (oben rechts) finden Sie den Button 'Demo-Menü'. Die Demo-Beispiele zeigen mögliche Bewegungs-Strategien – und geben einen Einblick in die Problematik kinematischer Überbestimmung.

Für Lernwillige

  • führt dieses Handbuch Schritt für Schritt durch die Möglichkeiten des 3D Gelenk-Baukastens. Sie finden eine Vielzahl von Möglichkeiten eine Bewegungsbahn selbst zu generieren oder aus einem CAD-System zu importieren. Zu Maskenfunktionen finden Sie ein "wie, warum und wozu"!
  • Ein "Kochbuch" im Anhang des Manuals zeigt (hoffentlich) praxisorientiert, wie die Demo-Datei generiert wurde. Diese Rezeptesammlung führt "Schritt für Schritt" (einschließlich kinematischer Stolperfallen & Lösungen) durch die Bewegungsprogrammierung.
Über die "normale" Knickarm-Robotik hinaus beherrscht der Programm-Algorithmus
- in der Länge veränderbare Teleskop-Achsen sowie
- kombinierte Portal & Knickarm Robotik


Parametrierung

  • Die Roboter-Mathematik dieses Baukastens ist entsprechend der mechanischen Roboter-Hardware individuell parametrierbar; mehr hierzu im orig. Handbuch / Kapitel Supervisor-Information.


Bildschirm- und Maskenaufbau

Bildschirm

  • Bildschirm oben links
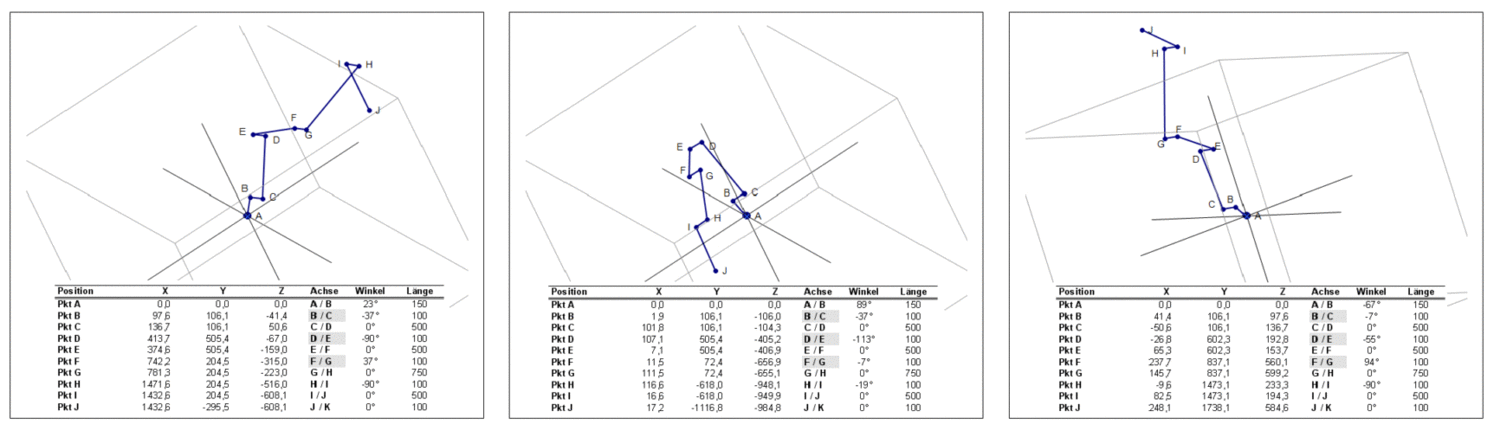
Grafik: Stilisierte Armstellung im 3D-Raum.
Der 3D-Raum ist kontinuierlich zwischen Maus & Vogelperspektive einstellbar. Die Einstellung hat keinen Einfluß auf die Berechnung.
- In der Grafik oben links der Button 'Control-Center', der die Maske aufruft.


  • Bildschirm oben rechts
ganz oben Perspektiv-Schieber, darunter die aktuellen XYZ Koordinaten aller Gelenke.


  • Bildschirm unten links / rechts
Kinematische Bewegungsdaten


Bedienerhinweise

  • Sprachumschaltung : Maske 'Start' (derzeit Deutsch / English, weitere Sprachen möglich).


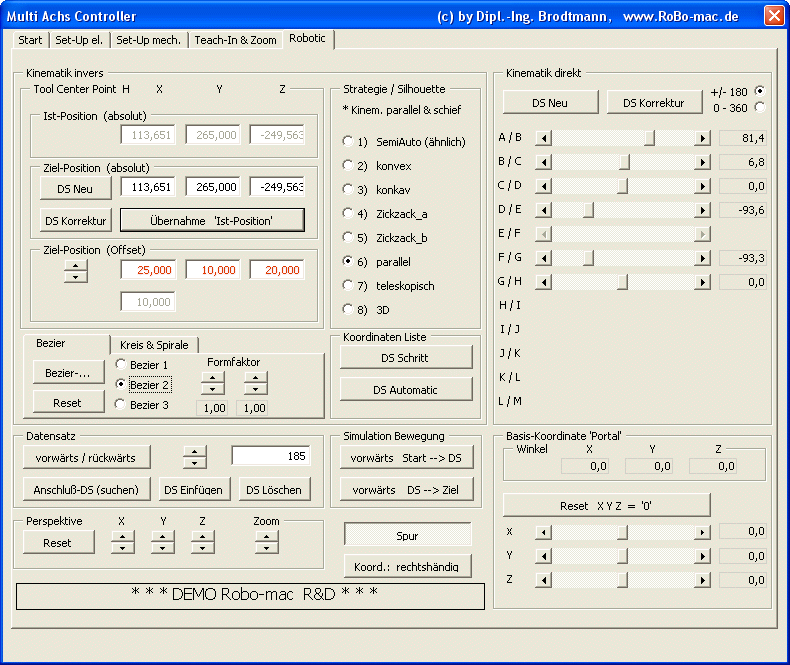
Maske 'Robotic'

Die Maske 'Robotic' mag zunächst "erschlagend" wirken, ermöglicht jedoch ohne Maskenwechsel nahezu alle kinematischen Funktionen und Befehle:

Direkte (vorwärts) Kinematik,

  • Berechnung der XYZ-Koordinaten des TCP aus Winkelstellung der Knickarme

Inverse (rückwärts) Kinematik

  • Berechnung der Knickarm-Winkelstellung aus vorgegeben XYZ-Koordinaten des TCP
  • freie, interaktive Off-line Entwicklung einer Bewegungsbahn
  • automatische Transformation einer extern vorgegeben Bewegungsbahn
  • 8 frei wählbare Bewegungsstrategien der Knickarme
  • sowie die Möglichkeit, Knickarm Roboter zusätzlich auf XYZ-Portal zu verfahren.

Last not lease

  • 3D-Visualisierung der Roboter Knickarme und einer Bewegungsspur des TCP aus frei wählbarer Maus- bis Adler-Perspektive.


Auch dieses Leistungsspektrum mag "erschlagen"; wir betrachten es schrittweise. Zunächst den Maskenaufbau. Grundsätzlich gilt: Sie können nichts kaputt machen – probieren Sie!

CNC+RoBo Maske Inv-Kinematik Deutsch 04.gif

Die Maske zeigt 3 Säulen,

links: inverse Kinematik & Bahngenerator, rechts: direkte Kinematik, Mitte: Zusatzfunktionen


Kinematik invers

alle Werte dieses Blocks (links oben) beziehen sich auf den TCP.

  • Die aktuelle Ist-Position wird im XYZ-Koordinatenfenster (ganz oben) angezeigt.
  • Ziel Position (absolut).
Der Wert wird im XYZ-Koordinatenfenster eingegeben.
Falls sinnvoll, kann der Ist-Wert zuvor ins Ziel-Feld kopiert (Übernahme 'Ist-Position') und danach geändert werden. Wahlweise wird diese Ziel Position als Neuer Datensatz (DS-Neu) hinzugefügt oder der aktuell gewählte Datensatz korrigiert (DS-Korrektur).
Die Achs-Winkelwerte werden hieraus OnLine errechnet und dem aktuellen Datensatz (s.u.) hinzugefügt.
  • Ziel Position (Offset).
Der Offset bewegt den TCP - bezogen auf seine aktuelle Position - stets um den gleichen Wert mit den Doppel-Pfeiltasten wahlweise vorwärts / rückwärts. Er ist entweder
  • als kartesischer Zielwert (XYZ) oder
  • als Vektor-Hub führ in eine teleskopartige 'Unter-Arm'-Bewegung definierbar.
Der aktive Offset färbt sich 'rot'.
  • Bezier
Diese Funktion ist in Vorbereitung; sie verbindet Teleskop-Bewegungen am Anfang und Ende einer Positionierbahn mit den "weichen Übergängen" einer Bezier-Kurve; vgl. Bezier, Hermite & Spline Interpolation


  • Datensatz
wählen Sie den zu bearbeitenden Datensatz mit seiner Ordnungs-Nr. oder den Pfeiltasten. Falls bereits mehrere Datensätze vorhandenen sind und Sie den letzten einer Liste aufrufen wollen, clicken Sie 'Anschluß DS (suchen)'. So Sie einen vorhandenen aus der Liste löschen oder einen zusätzlichen einfügen wollen, clicken Sie: 'DS-Neu' / 'DS-Löschen'.
Es kann sinnvoll sein, die Anfahr-Koordinaten eines Zieles vom Ziel aus gesehen "rückwärts" zu entwickeln. In der Praxis können hierbei zunächst 2 getrennte Bewegungsfragmente (Start-Fragment / Ziel-Fragment) entstehen, die es zu schließen gilt. Die Rast-Taste 'vorwärts / rückwärts' wählt in Zusammenarbeit mit 'Anschluß DS (suchen)' das entsprechende Fragment und dreht die Suchrichtung im 'Ziel-Fragment' um.


  • 3D-Perspektive & Zoom
wählen Sie mit den Doppel-Pfeiltasten die 3D-Perspektive. Der Knopf 'Reset' führt aus "unglücklichen" Perspektiven zurück in eine klassische 3D-Perspektive.


  • Bewegungsstrategie / Silhouette
Mehreren Bewegungsstrategien stehen zur Auswahl. Beispiele, wie diese Strategien arbeiten, finden Sie im Makro-Menü unter "Strategie-Demo…". Die gewählte Bewegungsstrategie bestimmt den Algorithmus der inversen Kinematik.
- Clicken Sie eine Strategie Ihrer Wahl. Im oberen Fenster-Bereich erscheint eine Info, ob diese für Parallel Kinematik, Schief Kinematik oder beide geeignet ist (vgl. Tutorial).
- Ein Wechsel zwischen den Bewegungsstrategien ist jederzeit möglich.
- Die Strategien 6 und 7 erzeugen ab Handgelenk-Punkt lineare Bewegungen und somit konstante Orientierung der Abtriebs-Achse.


  • Koordinaten Liste
Die Liste extern erzeugter XYZ Koordinaten des TCP wird - entsprechend der Bewegungsstrategie - in die Winkel der Knickarme transferiert; schrittweise oder automatisch für die gesamte Liste.


  • Simulation Bewegung
Die Bewegungssimulation visualisiert im zügigen Durchlauf die einzelnen Datensätze. Die bereits bekannte Rasttaste 'vorwärts / rückwärts' bestimmt die Laufrichtung:
Vorwärts: Start-Punkt bis zum aktuellen Datensatz / aktueller Datensatz bis Zielpunkt
Rückwärts: In umgekehrter Richtung.


  • Spur
Die Bewegungsspur des TCP läßt sich per Rasttaste zu/abschalten. Angezeigt wird die Spur zwischen Startpunkt und dem (beim Clicken der Taste) aktuellen Datensatz. Sie kann über die Tasten 'Simulation Bewegung' bzw. die Befehlsgruppe 'Datensatz' mit den Doppel-Pfeiltasten frei durchlaufen und so ein gesuchter Datensatz visuell gefunden werden. Mit Aufruf der Maske wird die Spur automatisch aktiviert – und kann ggf. abgeschaltet werden.


  • Stop
eine 'Stop-Taste' erscheint, sobald Simulation Bewegung oder Koordinaten Liste automatic gewählt ist. Die Funktion bricht ab, der Datensatz wird zum aktuellen Datensatz.


Kinematik direkt

Dieses Feld (rechts oben )zeigt Winkelschieber für 12 Achsen (A/B bis L/M) sowie den aktuell eingestellten Winkelwert, wahlweise im 0-360° oder -180° / +180° System. Nur die Schieber, die im Rahmen der Parametrierung aktiviert wurden, sind aktiv.
  • Die direkte Kinematik dient in erster Linie dazu, eine "vernünftige Startposition", die Orientierung des TCP-Trägerarmes als Ausgangspunkt der inversen Kinematik oder auch Stützpunkte zur Umfahrung eines Hindernisses manuell zu bestimmen. Man braucht sie selten, aber man braucht sie. Vieles ist hier Sisyphus & Try and Error.
  • Hat nach dem Gesetz der größten Gemeinheit Murphy zugeschlagen und die Knickarme stehen völlig daneben, so können die Schieber mit den Doppel-Pfeiltasten des Bereiches Datensatz auf die Werte des List-Datensatzes synchronisiert werden.
  • Ist in direkter Kinematik eine Winkelposition gefunden, so kann sie der Datensatz Liste über den Button 'Teach-In / Aktuelle Koordinaten' direkt zugeführt werden. Auch Kreisbewegungen sind so einfach erzeugbar.


  • Basiskoordinate Portal rechts unten
Koordinaten und Winkel-Berechnungen referenzieren auf den Achs-Fußpunkt XYZ.
  • Komplexe Robotersysteme arbeiten mit verfahrbarem Fußpunkt auf XYZ-Portal. Der Algorithmus inverser Kinematik berücksichtigt bei der Knickarm Berechnung die in direkter Kinematik vorgewählte Portal-Kordinate.
  • Die Verschiebung der Basiskoordinaten ermöglicht es auch, eine feste Fußpunkt Position entsprechend den kinematischen Möglichkeiten der Roboter-Mechanik zu optimieren.


  • Button 'DS Neu' & 'DS Korrektur'
Sie finden diese Funktionen in den Bereichen inverse sowie direkte Kinematik.
Per 'DS Korrektur' ändern Sie den aktuellen Datensatz, 'DS Neu' generiert einen zusätzlichen Datensatz am aktiven Ende eines Datensatz-Blocks.
Unter Sicherheitsgesichtspunkten ist 'DS Neu' de-aktiviert, sobald der aktuell gewählte Datensatz sich nicht am Block-Ende befindet; gleichsinniges gilt für die Offset Doppel-Pfeiltasten. Wollen Sie größere Änderungen vornehmen, so sollten Sie (im Feld 'Datensatz')
  • per 'DS Einfügen' einen Datensatz an aktueller Stelle einfügen,
  • per 'Anschluß DS suchen' das aktive Ende des Blockes (vorwärts/rückwärts) aufsuchen.
Die Taste 'DS Neu' wird aktiviert.


Koordinaten & Datensatz-Liste

Im unteren Teil des Bildschirmes werden (ab Zeile 51) die Kinematischen Bewegungsdaten zeilenweise gespeichert; links die XYZ-Koordinaten, rechts deren korrespondierende Winkel. Über die Maske haben Sie direkten Zugriff auf bereits erstellte oder entstehende Datensätze sowie deren Korrektur. Die in der Maske angezeigte Ordnungs-Nr. des Datensatzes wird mit dem Cursor ergänzend markiert. Sie finden:

Spaltenbereich 1 / (A) Ordnungs-Nr. der Bewegungsstrategie
Spaltenbereich 2 bis 4 / (B bis D) Soll-Koordinate XYZ des TCP (absolut)
Spaltenbereich 5 / (E) Soll-Vektor-Offset des TCP (relativ)
Spaltenbereich 7 bis 9 / (G bis I) Ist-Koordinate XYZ Portal / Fußpunkt *)
Spaltenbereich 14 bis 16 / (N bis P) Ist-Koordinate XYZ des TCP (absolut)
Spaltenbereich 39 bis 50 / (AM bis AX) Winkelwerte Achsen (A/B bis L/M)

Portal / Fußpunkt Ist-Koordinate

  • Sind in der Liste keine Fußpunkt-Koordinaten vorhanden, so arbeitet der Algorithmus "mit 0-Wert". Arbeiten Sie mit dem Bahn-Generator, so werden Portal Koordinaten in der Koordinatenliste nur ausgewiesen, wenn sie von 0 abweichen.
  • Sind Fußpunkt-Koordinaten in der Liste vorhanden, so werden sie als Offset berücksichtigt.


Bahnsteuerung

CAD-Import

Sind Soll-Koordinaten (z.B. aus einem CAD-Programm) vorhanden, so werden sie zunächst mit den Excel-üblichen Befehlen in den Bereich der Sollkoordinaten (Spalten 2 bis 4 / bzw. B bis D) des Datenmoduls ab Zeile 50 übertragen. Das Programm generiert aus diesen TCP Soll-Koordinaten entsprechend der gewählten Bewegungsstrategie (s.u.) die Winkelstellung der Knickarme und schreibt sie in das Bewegungsprotokoll. Hierzu werden die Koordinaten entweder über den Button 'DS-Schritt' (Step by Step) aufgerufen oder per 'DS-Automatic' als Datenblock verarbeitet.

Bahngenerator

Sind keine (extern ermittelten) Soll-Koordinaten vorhanden, so müssen sie interaktiv generiert werden (Offline Teach-In). Die TCP-Bahn-Stützpunkte werden wahlweise als XYZ-Wert Absolut oder als Offset eingegeben und per 'DS Neu' bzw. 'DS Korrektur' verarbeitet. Der Bahngenerator

- visualisiert "Real-time" die Bewegung im 3D-Raum entsprechend der gewählten Bewegungsstrategie (s.u.)
- erlaubt hierbei beliebig "Try & Error" und
- erzeugt die XYZ-Koordinatenliste des TCP sowie das Knickarm-Bewegungsprotokoll.


CAD-Import und Bahngenerator greifen auf die gewählte Bewegungsstrategie zurück und ermöglichen eine kontinuierliche oder schrittweise Kontrollfahrt. Bestimmen Sie ggf. in direkter Kinematik eine "vernünftige" Startpositionierung.


  • Im Rahmen einer interaktiven Arbeitssitzung erzeugt/speichert das Programm ein Bahnprofil mit Koordinaten und Winkelwerten. Wurden diese mit dem Bahngenerator erzeugt, so kann aus den gewonnenen Ist-Koordinaten eine ähnliche "parallel versetzte" Bahn mit den EXCEL-üblichen Befehlen "recht bequem" generiert werden: Die per Bahngenerator erzeugte Ist-Koordinatenliste wird mit entsprechendem Offset in den Soll-Koordinaten Bereich übertragen und über den Button 'DS-Schritt' bzw. 'DS-Automatic' erneut verarbeitet.
  • Stellt sich heraus, daß ein Zielpunkt außerhalb der kinematischen Möglichkeiten liegt und daß das Problem durch verschieben des Roboter 'Schulter bzw. Fußpunktes' zu lösen sei, so muß nicht die bisherige Arbeit erneuert werden: Über den Portal-Offset wird eine neue Basisposition gewählt und über den Button 'DS-Schritt' bzw. 'DS-Automatic' ein neues Bewegungsprofil bei geändertem Fußpunkt erzeugt.
  • Der Portal-Offset ist im Masken Bereich der 'direkten Kinematik' korrigierbar.
- Der hier eingegebene Wert wird für den aktuellen Datensatz in der Koordinaten-Liste gespeichert. Clicken Sie hierzu den Button 'DS Korrektur' bzw. 'DS Neu'.
- Um den bisherigen Portal-Offset beizubehalten, clicken sie den 'Doppelpfeil' "rauf/runter" (im Feld Datensatz) je einmal, der bisherige Offset wird synchronisiert.

TCP Spur

Die Grafik visualisiert aus beliebiger Perspektive die aktuell errechnete Winkelstellung der Knickarme im 3D-Raum und (zu-/abschaltbar) die Bewegungsspur des TCP. Die Perspektiv-Einstellung hat keinen Einfluß auf die kinematische Berechnung.


Bewegungsstrategien

Um trotz Überbestimmung aus theoretisch unendlich vielen Winkel-Kombinationen möglichst geeignete Vektorlagen der Roboterarme zu berechnen verfolgt der RoBo-mac Gelenkbaukasten mehrere, frei wählbare Bewegungsstrategien:

  • Semi-Automatic präzisiert manuelle Winkel-Vorwahl "in ähnlicher Silhouette"
  • Konvex: Das mittlere Arm-Element liegt oberhalb des Zielpunktes
  • Konkav arbeitet vice versa zu Konvex
  • Zickzack: Die Arm-Elemente bilden eine Zickzack Silhouette
  • Parallel, bewegt den Übergangspunkt "Arm/Handgelenk" parallel
  • Teleskope bewegt Knickarme transversal wie Teleskoparme.

Zwischen den Strategien kann beliebig gewechselt werden.

Semi-Automatic

orientiert sich an der Ist-Position der Gelenke und erreicht die neue Zielposition "in ähnlicher Silhouette". Wird die Arm-Position mit den Schiebern "in etwa" vorgewählt, so ermittelt der Algorithmus die Vektorlagen der Arme mit o.g. Präzision, ein Hindernis kann mit der Halb-Automatic so umfahren werden. Die Stützpunkt-Schrittweite beeinflußt die "Ähnlichkeit" der Silhouette; liegen die Stützpunkte weit auseinander, so geht die Ähnlichkeit verloren. Die Bahnen der Gelenkpunkte sind bei Hin- und Herbewegung selten kongruent.


Konvex, Konkav & Zickzack

sind Voll-Automatic Funktionen, sie generieren die Bahn mit reproduzierbarer Winkelstellung der Gelenke - unabhängig von deren Ausgangs-Position; diese Bewegungsstrategien ermitteln für alle Gelenkpunkte stets die gleiche Bahn. Der Algorithmus eignet sich für Bewegungen, denen genügend Arbeitsraum zur Verfügung steht, er benötigt wenige Stützpunkte.

Innerhalb jeder einzelnen Bewegungsstrategie verlaufen die Armbewegungen konsistent und erwartungsgemäß.

  • Ein Strategiewechsel ist jederzeit möglich, führt jedoch über eine im Detail undefinierte Streck-Bewegung des Armes. In dieser Bewegungsphase besteht erhöhte Kollisionsgefahr.


Parallel & Teleskope

ähneln o.g. Voll-Automatic Funktionen. Der "Unter-Arm" mit dem Übergangspunkt "Arm/Handgelenk" wird parallel zu sich selbst, bzw. in der Vektororientierung seiner eigenen Achse bewegt. Die Bewegungsstrategie 'teleskopisch' verwendet hierzu keinen absoluten oder relativen XYZ-Wert, sondern einen Vektor-Hub. Die Ist-Vektorlage des "TCP Trag-Armes" wird um diesen Hub verschoben. Im Ergebnis führt dies zu einer teleskopartigen Bewegung.

  • Die Winkelorientierung aller kaskadisch folgenden Achsen bleibt erhalten.
  • Ein Strategiewechsel ist jederzeit ohne erhöhte Kollisionsgefahr möglich. Der Arbeitsbereich ist kleiner als der anderer Strategien.


Bézier-Generator

Bézier Kurven haben die wunderbare Eigenschaft, nicht nur 2 Punkte zu verbinden:

  • Die Kurve läßt sich in weiten Grenzen mit mathematisch gut beherrschbaren "Anfassern" beliebig formen. Besonders hilfreich ist es, daß die Bézier Kurve ihre "Anfasser" punktgenau tangential verläßt bzw. tangential einläuft, vgl. Tutorial.
  • Liegen die Anfasser in der Vektor-Orientierung einer anderen, anschließenden Kurve oder Geraden so gehen beide nahtlos ineinander über. Anders ausgedrückt:
  • Zwei gegebene Bahn-Segmente, können durch Bézier-Splines "glatt" verbunden werden.

Soweit die Theorie. Mehr hierzu unter: http://www.cnc-mac.de/html/bezier___spline_.html.


In der Praxis bedarf es erheblicher Übung, mit den Anfassern eine "vernünftige" Kurve zu generieren. Wir überlassen dies dem Bahngenerator.

Der Bahngenerator fügt eine Bézier Kurve mit 20 Stützpunkten ein, die Ihnen zur Beurteilung zunächst lediglich in der 3D-Grafik gezeigt wird. Im Sinne besserer Übersichtlichkeit werden alle anderen Bewegungsbahnen bis auf diese Kurve ausgeblendet.

  • Der Bahngenerator bestimmt aus der Vektorlage der zu verbindenden Bahn-Segmente deren Tangentenlage im 3D Raum und berechnet 3 Vorschlagsformen der Kurve, die Sie per Click auswählen oder individuell per Schieber ändern können. Die Grundform dieser Basis-Kurven ist vom Öffnungswinkel zwischen den Tangenten abhängig.


Bei einem Öffnungswinkel von 90° und

  • gleichem Abstand zum theoretischen Schnittpunkt erzeugen Kurve 1) und 2) einen exak-ten ¼ Kreis. Kurve 3) bildet eine Sehne.
  • unterschiedlichem Abstand erzeugt Kurve 1) ein Oval, Kurve 2) eine Ellipse. Kurve 3) bildet eine Sehne.


Bei anderen Öffnungswinkeln kommt die Vielfalt Béziers zum Tragen:

  • Kurve 1) verbindet die Bahn-Segmente bei beliebigem Öffnungswinkel jedoch gleichem Abstand zum theoretischen Schnittpunkt mit einem Kreissegment.
  • Tendenziell erzeugt Kurve 2)
- bei flachen Öffnungswinkeln flachere Verrundungen als Kurve 1),
- bei spitzeren Öffnungswinkeln spitzere Verrundungen als Kurve 1).
  • Liegen die Tangenten der zu verbindenden Segmente parallel, so erzeugt Kurve 1) einen Halbkreis, Kurve 2) eine Halb-Ellipse.
  • Kurve 3) "reagiert stärker" auf Änderungen des Öffnungswinkels und der Schnittpunktlage als die beiden anderen; dies kann in sehr "elegante" aber auch völlig unbrauchbare Kurven führen.

Liegen zu verbindenden Bahnsegmente "parallel versetzt" (oder auch "schräg versetzt"), so werden sie mit einem "S-Bogen" verbunden; die Ausprägung des "S-Bogens" ist bei den 3 Kurven recht unterschiedlich.

Falls Sie die Kurvenlage ändern möchten, korrigieren Sie die Stützpunkte.


Bézier "Wunschbahn"

Bézier Kurven laufen hoch präzise in ihren eigenen Tangentenpunkt ein; die Kurve selber ist, wenngleich exakt reproduzierbar jedoch nur bedingt auf eine "exakte Wunschbahn" zu brin-gen. Für die Bedienung des Bahngenerators bedeutet dies, zwischen 'bestimmter' und 'unbe-stimmter' Bewegungs-Bahn zu unterscheiden. Die 'bestimmte' Bewegungs-Bahn ermöglicht einen präzis geführten Werkzeugeingriff, die 'unbestimmte' Bahn dient vorzugsweise einer "eleganten" Werkzeugbewegung im Raum ohne Werkzeugeingriff. Bahnsegmente mit Werk-zeugeingriff generieren Sie in 'Inverser- Kinematik' mit den Bewegungsstrategien 1) bis 8).

  • Muß die "Wunschbahn" Bahn präzise über einen oder mehrere bestimmte Raumpunkt geführt werden, so teilen Sie die Bahn in Segmentabschnitte. Mehrere Bézier Kurven ver-binden diese Raumpunkte als "Cascadierter Spline". Ein gemeinsames Stützpunkt-Paar bestimmt die Orientierung der ein- und auslaufenden Kurve. CAD/CAE Systeme arbeiten auf dieser Technologie-Basis. Vgl. http://www.cnc-mac.de/html/bezier___spline_.html.


Bézier-Kreise, Ellipsen & Spiralen

sind als Cascadierter Spline mit hoher Präzision möglich.

  • Ab 3 Raumpunkten läßt sich ein nahezu exakter Vollkreis, ab 4 Raumpunkten eine Ellipse bzw. Spirale mit den Vorschlagswerten des Bahngenerators formen. Der Bahngenerator arbeitet für alle 3 "Kreisvarianten" mit cascadierten ¼ Kreisen. Abweichung zur "echten" Bahn liegen im 1/10 Promille-Bereich.
  • Ellipsen und Spiralen sind auf einen Kreis zurückzuführen, dessen Radius sich mit dem Drehwinkel ändert. Per Button 'Bézier- Spirale' teilen Sie dem Generator mit, die Tangentenorientierung aus dem Steigungswinkel der Spirale zu berechnen.
  • "Spiralbewegungen" werden aus ¼ Kreisen zusammengesetzt. Soll die Spirale von innen nach außen laufen, so erhöht sich der Radius jedes "End-Kreis ¼" gegenüber seinem jeweiligen "Start-Radius" um ¼ der gewünschten Steigung. Der Bahngenerator berechnet hieraus den Steigungswinkel der Tangenten.

Im Kochbuch Inverse Kinematik finden Sie eine "Schritt für Schritt" Anleitung.


Bézier-Bahn & Arbeitsbereich

Der Bézier Kurven Generator prüft, ob die vorgeschlagene Kurve im Arbeitsbereich des Roboters liegt. Ob diese Kurve in 'Inverser Kinematik' durch den Roboterarm realisiert werden kann, hängt von den parametrierten Grenzwinkeln ab (vgl. Supervisor-Information). Die Algorithmen der 'Inversen Kinematik' melden ggf. eine 'Winkelwert Überschreitung'.

Falls die Kurve in eine 'Winkelwert Überschreitung' führt, haben Sie 2 Korrekturmöglichkeiten:

  • Stauchen Sie die Kurve mit den Schiebern bzw.
  • Fahren Sie den Zielpunkt nicht über den kürzesten Weg an, sondern drehen Sie die Arme über die "Winkelposition 0°" zurück. Führen Sie den Roboterarm hierzu über "Hilfs-" Raumpunkte in die Ziel-Position.


Positionierung & Orientierung

  • Die Positionierung bestimmt die kartesische XYZ-Position des "End-Effektors" im Raum,
  • die Orientierung unter welchen Winkeln er steht.

Beide Werte zusammen definieren seine Vektorlage.

Bedienungshinweis

  • Muß bei Beibehaltung der Position die Orientierung korrigiert werden, so wird zunächst per Button 'Übernahme Ist-Position' diese "vorgemerkt".
  • In Direkter Kinematik wird die gewünschte Orientierung gewählt.

Hilfreich hierbei ist die Koordinaten-Übersicht unmittelbar rechts neben der Grafik. - Für eine senkrechte Orientierung der Achse G/H sind deren X und Z-Koordinaten gleich, - für eine horizontale die Y-Koordinaten.

  • Die Um-Orientierung führt zunächst in eine Änderung der Position. In Inverser Kinematik wird die "vorgemerkte" Position in der gewählten Orientierung mit 'Strategie 6) parallel' angefahren.

Zweckmäßiger Weise wird der "mit richtiger Orientierung aber falscher Position" in 'Direkter Kinematik' erzeugte Zwischenschritt nicht als Datensatz gespeichert und nachträglich korrigiert, sondern im Feld 'Zielposition absolut' der Butten 'DS Neu' sofort geklickt.

  • Bitte beachten Sie, daß eine Um-Orientierung bei großer Schrittweite (horizontal / senk-recht) über undefinierte Detail-Bewegung führen kann. Legen Sie diese Bewegungsphase in einen unkritischen Bewegungsbereich.


Kombinierte Portal & Knickarm Robotik

Ist ein Knickarm Roboter auf Portal verfahrbar, so überlagern sich beide Bewegungskomponenten. Dies erhöht die Anzahl der Freiheitsgrade enorm. Um trotzdem gezielt Einfluß auf die Kinematik nehmen zu können, referenziert die Berechnung der Knickarm-Winkel auf die aktuelle Fußpunkt Position.

  • Wählen Sie eine Fußpunktposition in direkter Kinematik und
die XYZ-Zielkoordinate des TCP im Maskenbereich der inversen Kinematik.
  • Beide Bewegungskomponenten lassen sich so zu einer komplexen Gesamtbewegung kombinieren – und bestimmen die Orientierung des TCP.


Soll die TCP Position bei geänderter Fußpunkt Koordinate beibehalten werden, so

- clicken Sie zunächst den Button 'Übernahme Ist-Position' (Feld 'Zielposition absolut'),
- korrigieren Sie die Fußpunkt Koordinate,
- clicken Sie 'DS Neu' (Bereich direkte Kinematik)
- clicken Sie 'DS Korrektur' (im Feld 'Zielposition absolut').
  • Diese Orientierungsänderung bei gleicher XYZ-Position führt in eine "Biege-Bewegung".


Positionierfehler & Watchdog

Unabhängig davon, wie die Soll-Werte erzeugt wurden, werden die Datensatz Ist-Werte in inverser Kinematik entsprechend der gewählten Bewegungsstrategie berechnet und als korrespondierende Knickarm-Winkel gespeichert. In direkter Kinematik wird aus diesen Knickarm-Winkeln der XYZ-Wert des TCP errechnet. Das Verfahren mag umständlich sein, ermöglicht jedoch einen Soll/Ist Vergleich. Die absoluten Positionierfehler Soll/Ist des TCP liegen unter 1/10.000 mm, meist in einer Größenordnung von 10-5 bis 10-6 mm.

Ein Watchdog-Algorithmus überwacht intern die Soll/Ist-Abweichung und schlägt ggf. Alarm. Falls der Zielpunkt nicht berechenbar oder kinematisch nicht erreichbar ist, wird eine Fehlermeldung generiert.


Kinematische Bewegungsebenen

Parallele Ebenen

Die Algorithmen der bisher besprochenen Bewegungsstrategien erwarten, daß sich die Schwenkachsen zwischen Schulterpunkt und Ellbogen bzw. dem Übergangspunkt "Arm/Handgelenk" in parallelen Ebenen bewegen. Die An- und Abtriebsachsen A/B bzw. G/H dürfen Drehachsen sein. Diese Parallel-Kinematik (vgl. Tutorial) erreicht jeden beliebigen Raumpunkt (XYZ).


Schiefe Ebenen

Die zusätzliche Drehmöglichkeit einer Schwenkachse zwischen Schulterpunkt und Handgelenk erhöht die Bewegungsvielfalt enorm. Dieser Vorteil wird mit einer komplexen Mechanik sowie einer nochmals gesteigerten kinematischer Überbestimmung erkauft; der Rechenaufwand steigt extrem – und führt in wahrnehmbare Rechenzeit. Es müssen 3D- Näherungsalgorithmen verwendet werden (vgl. Tutorial).

Näherungsalgorithmen haben stets einen Gültigkeitsbereich, der hier von Start- & Zielposition sowie der Bewegungsstrategie abhängt. Nicht jede Zielposition ist aus jeder Startposition erreichbar, ggf. muß die Bewegungsstrategie geändert bzw. die Startposition im Rahmen der Bahnoptimierung (Interaktiver Prozeß) zuvor korrigiert werden.

Der Gültigkeitsbereich bildet sich aus Schnittmengen vorgenannter Parameter. Ein Watchdog-Algorithmus überwacht, daß sich die Näherungsalgorithmen im Gültigkeitsbereich bewegen; er generiert ggf. eine Fehlermeldung & Korrekturempfehlung. Die Standardabweichung der absoluten Positionierfehler Soll/Ist liegt in der Größenordnung "einiger Hundertstel".

  • Die Näherungsalogrithmen beherrschen die Bewegungsstrategien 5 und 6 (bevorzugt) sowie eine spezielle 3-D Strategie 8. Sie ermöglicht höhere Drehwinkel der Armachsen bei kleinerem Arbeitsbereich.

Das Programm prüft selbstständig, ob der rechenintensive Schief-Algorithmus erforderlich wird oder der schnellere & präzisere Parallel-Algorithmus geeignet ist.


Theorie & Praxis

Dieser Praxis orientierte Artikel ist ein produkt-neutralisierter Handbuch-Auszug.

  • Im Orig. Handbuch finden Sie Supervisor-Informationen, wie das Programm der Mechanik-Struktur Ihres Gelenkarmroboters und dessen Maßen angepaßt wird, so daß die Mathematik des 3D Gelenk-Baukasten und Roboter-Mechanik kongruent sind. Die mathematischen Positionierfehler liegen dann in einer Größenordnung von 10-5 bis 10-6 mm - und dies ist gewiß eine Herausforderung an die Robotermechanik!
  • Im Anhang zum Handbuch ein "Kochbuch" Inverse Kinematik. Diese Rezeptesammlung führt "Schritt für Schritt" (einschließlich kinematischer Stolperfallen & Lösungen) durch die Bewegungsprogrammierung.
  • Theoretischen Background erläutert Teil 1 dieses Artikels Inverse Kinematik 1 – Theorie (Tutorial).


Weblinks


Mehr dazu unter

All dies muß getestet werden, ich habe hierzu OKTAVIAX, den Acht-Achser entwickelt; unter 

 http://www.youtube.com/watch?v=TT344LsOnuY

macht er ein Tänzchen (Bitte Lautsprecher einschalten).


NLB

Von „https://rn-wissen.de/wiki/index.php?title=Inverse_Kinematik_2_–_Praxis&oldid=27849“

LiFePO4 Speicher Test