(→Graue Katzen) |
(→Tabelle der Faltungskerne) |
||
| Zeile 279: | Zeile 279: | ||
|- | |- | ||
|<math> | |<math> | ||
| − | |||
\begin{pmatrix} | \begin{pmatrix} | ||
1 & 2 & 1 \\ | 1 & 2 & 1 \\ | ||
| Zeile 289: | Zeile 288: | ||
|- | |- | ||
|<math> | |<math> | ||
| − | |||
\begin{pmatrix} | \begin{pmatrix} | ||
1 & 0 & -1 \\ | 1 & 0 & -1 \\ | ||
| Zeile 299: | Zeile 297: | ||
|- | |- | ||
|<math> | |<math> | ||
| − | |||
\begin{pmatrix} | \begin{pmatrix} | ||
1 & 1 & 1 \\ | 1 & 1 & 1 \\ | ||
| Zeile 309: | Zeile 306: | ||
|- | |- | ||
|<math> | |<math> | ||
| − | |||
\begin{pmatrix} | \begin{pmatrix} | ||
-1 & -1 & 1 \\ | -1 & -1 & 1 \\ | ||
Aktuelle Version vom 31. August 2006, 13:23 Uhr
In diesem Tutorial möchte ich einen Einstieg in die Bildverarbeitung für alle Interessierten bieten. Die zwei Kapitel, die momentan fertig sind, habe ich schon vor einiger Zeit erstellt. Je nach meiner freien Zeit werde ich versuchen, dieses Tutorial weiter auzubauen. Vorschläge und Fragen bitte auf die Seite Diskussion. Zefram 17:42, 22. Dez 2005 (CET)
Inhaltsverzeichnis
Farbräume - Warum nachts alle Katzen grau sind
In diesem Kapitel geht es um scheinbar selbstverständliches: Um Farben.Wir werden eine neue Möglichkeit der Darstellung von Farben kennenlernen und schließlich auch die Frage nach den grauen Katzen beantworten können.
Forty Shades of Green - RGB
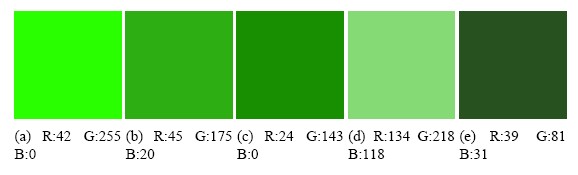
Jeder weiß wohl wofür RGB steht. Die Abkürzung bezeichnet das Format, in dem normalerweise die Farben der Pixel eines Farbbildes kodiert werden. Pro Pixel geben uns drei Zahlen die jeweilige Intensität jedes der drei Farbkanäle rot, grün und blau an. Was HSV ist, werden wir gleich sehen. Schauen wir uns in der untigen Tabelle mal einige Grüntöne und die zugehörigen RGB-Werte an.
Nun stellen wir uns vor, wir sollen anhand der RGB-Werte alle grünen Objekte im Bild finden. Nix leichter als das, oder? Wir schauen einfach Pixel für Pixel an und entscheiden anhand der RGB-Werte, ob es sich um einen grünen Bildpunkt handelt, oder nicht. Aha, dann mal los.
Zuerst brauchen wir also ein Kriterium, anhand dessen wir festlegen, was "grün" ist, und was nicht. Wir werden schnell feststellen, dass das garnicht so einfach ist, denn wie man sieht, schwanken die RGB-Werte bei den Grüntönen hier unten doch erheblich. Betrachten wir auch Abbildung 1.1.
Das Bild zeigt einen bunten Fußboden und darauf einige Objekte, die von der Bildverarbeitung erkannt werden sollen. (Nein, das Bild habe ich nicht in meinem Wohnzimmer aufgenommen, sondern in einem Labor unserer Uni. Der Fußbodenbelag ist eine Antiquität aus der Gründerzeit, die ich mir garnicht leisten könnte.) In der Tat ist ein solch gemusterter Fußboden für die Bildverarbeitung eine Katastrophe. Die RGB-Werte springen wie wild, da sich viele verschiedene Farbtöne in dem Muster befinden. Jetzt schauen wir mal das rechte Bild an.
Erstmal ist das Bild offensichtlich schwarz/weiß. Außerdem haben die Fußboden- Pixel so ziemlich alle den selben Grauwert und die Objekte heben sich deutlich vom uninteressanten Hintergrund ab. Das sieht doch schon besser aus, da könnte unsere Bildverarbeitung was draus machen.
HSV
Das Geheimnis: Wir haben nicht einfach ein s/w-Bild erzeugt, sondern haben das Bild vom RGB-Farbraum in den HSV-Farbraum überführt. Beim HSV-Farbraum wird jeder Pixel wieder mit drei Werten codiert (3 Kanäle). Also genau wie bei RGB. Allerdings haben wir jetzt einen Kanal für den Farbwert (Hue), einen für die Sättigung (Saturation) und eine Art Helligkeitsbeiwert (Value). Daher also die Abkürzung HSV. Das rechte Bild zeigt nur einen der drei Kanäle, nämlich den Hue-Kanal (Farbwert).
Was hat es nun mit diesen drei Kanälen auf sich? Das HSV Farbmodel ist sehr intuitiv. Erinnert euch mal an den Kunst-Unterricht in der Schule. Wenn man eine Farbe zusammenmischen will nimmt man sich zunächst mal eine Grundfarbe aus dem Farbkasten. Nehmen wir zum Beispiel ein schönes Grün. Diese Grundfarbe ist der Hue-Wert in HSV. Jetzt wollen wir das grün etwas aufhellen und mischen Weiß dazu. Je mehr Weiß, desto heller wird die Farbe. Mischen wir viel Weiß dazu, erhalten wir einen Pastell-Farbton. Bei noch mehr Weiß erhalten wir eine Art Grauton. Der Weiß-Anteil wird in HSV mit dem zweiten Kanal, der Sättigung codiert. Der dritte Kanal funktioniert ähnlich, nur dass wir hier Schwarz statt Weiß beimischen.
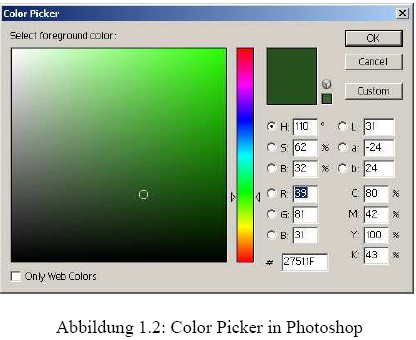
Am besten, ihr startet mal Photoshop oder eine ähnliche Software und spielt mal ein wenig mit der Farbauswahl herum. Denn auch dort kommt das HSV-Modell (oder zumindest eine Abart davon) zum Einsatz. Abbildung 1.2 zeigt das Farbauswahl-Tool von Photoshop. In dem farbigen Balken kann man sich den Hue (Farbwert)-Kanal festlegen. In dem großen Quadrat daneben wird der Saturation (horizontal) und Value (vertikal) festgelegt. Obwohl dabei eine Menge unterschiedlicher Farben entstehen, haben alle eine Gemeinsamkeit: Der Hue-Wert ändert sich nicht.
Schaut nochmal oben in das Bild 1.1. All diese Grüntöne haben den selben Hue-Wert. Und auch der Fußbodenbelag im Bild aus dem Labor hat überall einen ähnlichen Hue-Wert. Offensichtlich ist der HSV-Farbraum dem RGB weit überlegen, wenn es darum geht, bestimmte Farben im Bild zu finden. Aufgrund seiner Eigenschaften ändert sich der H-Wert eines Objektes auch bei wechselnden Beleuchtungsverhältnissen kaum, was ein großer Vorteil gegenüber RGB ist. Da HSV offenbar so gut ist, brauchen wir noch ein Verfahren, unser RGB-Bild nach HSV umzurechnen.
Von RGB zu HSV
Der folgende Algorithmus (Pseudo-Code) zeigt die Umrechnung von RGB nach HSV. Viel mehr ist dazu auch nicht zu sagen.
function RGBtoHSV(pixel RGB): pixel
{ variable minimum,maximum, delta;
pixel HSV;
minimum=min(RGB.r, RGB.g, RGB.b);
maximum=max(RGB.r, RGB.g, RGB.b);
delta=maximum-minimum;
HSV.v=maximum;
if (HSV.v==0) then HSV.s=0;
else HSV.s=delta*(255/HSV.v);
if (HSV.s==0) then HSV.h=0;
else
{ if (maximum==RGB.r) then
HSV.h=60.0*(RGB.g-RGB.b)/delta;
else if (maximum==RGB.g) then
HSV.h=120+60.0*(RGB.b-RGB.r)/delta;
else if (maximum==RGB.b) then
HSV.h=240+60.0*(RGB.r-RGB.g)/delta;
if (HSV.h<0) then HSV.h+=360;
//HSV.h hat noch einen Wertebereich von 0..360
//darum jetzt auf 0..255 normieren
HSV.h=HSV.h*255/360;
}
return HSV;
}
Graue Katzen
In diesem Kapital haben wir den HSV-Farbraum und seine Vorteile gegenüber RGB kennengelernt. Ein Punkt ist aber noch offen: Warum sagt der Volksmund, dass nachts alle Katzen grau sind? Ist da etwas dran?
Nun, im menschlichen Auge sind prinzipiell zwei Arten von Zellen für das Sehen verantwortlich. Die sog. "Zapfen" sind für das Farbsehen zuständig. Es gibt drei Arten von diesen Zapfen: Manche sind besonders für rotes Licht empfindlich, andere für grünes und die dritte Art ist für Blau zuständig. Die zweite Sorte von Zellen sind die "Stäbchen". Sie können keine Farben unterscheiden, sondern reagieren nur auf Hell/Dunkel-Reize.
Nun brauchen die farbempfindlichen Zapfen aber relativ viel Licht, um arbeiten zu können. Sie sind also für das Sehen bei Tag zuständig, bei Dunkelheit liefern sie keine Signale. Die farbunempfindlichen Stäbchen hingegen sind sehr empfindlich und kommen auch mit sehr wenig Licht klar. Deshalb sehen wir im Dunkeln oder in der Dämmerung hauptsächlich oder ausschließlich mit den Stäbchen, die aber keine Farben wahrnehmen können. Dem Gehirn fehlt also die Farbinformation, wir sehen schwarz/weiß. Und darum sind eben nachts (nicht nur) alle Katzen grau.
Von Falten und Kanten - Lineare Faltung
In diesem Kapitel nutzen wir die Kantenerkennung als Motivation, um uns mit den sogenannten "Linearen Faltungen" eine Menge Möglichkeiten bei der Bildverarbeitung zu erschließen.
Vom Bild zur Kante - Kantenerkennung leicht gemacht
Der Begriff "Lineare Faltung" klingt erstmal furchtbar kompliziert. Ich kann euch aber beruhigen, das Verfahren ist ganz einfach. Wer ein paar Zahlen addieren kann, der kann auch eine effiziente Kantenerkennung durchführen. Mehr als eine handvoll Additionen und Multiplikationen braucht man nämlich nicht, wie wir gleich sehen werden.
Eine Faltung ist eine binäre Operation. Das hat nix mit Binärzahlen zu tun, sondern bedeutet, dass zwei Operanden gebraucht werden. Klingt kompliziert? Ist es aber nicht. Die Addition zum Beispiel ist auch eine binäre Operation, denn wir brauchen zwei Operanden: Operand1 + Operand2.
Ok, was sind nun die beiden Operanden für die Faltung? Ganz einfach: Wir brauchen ein Bild (wer hätte das gedacht) und als zweiten Operanden einen sogenannten Faltungskern. Dieser Faltungskern bestimmt, wie das Ergebnis der Faltung aussieht. Anderer Kern, anderes Ergebnis. Klar, bei der Addition kommt auch eine andere Summe raus, wenn ich einen Summanden ändere. Als erstes brauchen wir also ein Bild. Voilá, hier ist es: [math] \begin{pmatrix} \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots \\ \dots & 20 & 20 & 20 & 100 & 100 & 100 & \dots \\ \dots & 20 & 20 & 20 & 100 & 100 & 100 & \dots \\ \dots & 20 & 20 & 20 & 100 & 100 & 100 & \dots \\ \dots & 20 & 20 & 20 & 100 & 100 & 100 & \dots \\ \dots & 20 & 20 & 20 & 100 & 100 & 100 & \dots \\ \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots & \vdots \\ \end{pmatrix} [/math]
Ok, das ist natürlich nur ein Ausschnitt aus der Mitte des Bildes. Wir stellen fest, dass in den ersten drei Spalten alle Pixel fast schwarz sind (sie haben den Wert 20, also ein sehr dunkles grau). Die folgenden Pixel mit Farbwert 100 sind etwas heller. Wir haben es hier also mit einer fantastischen Kante zu tun, die nur darauf wartet, von unserem Algorithmus entdeckt zu werden. Aber soweit sind wir noch nicht. Also schnell weiter zum Faltungskern. So ein Kern sieht aus wie ein kleines Bild (wir sagen auch "Matrix" dazu) und hat meist die Größe 3x3. Also 3 Spalten und 3 Zeilen. Hier ist mal so ein Kern:
[math] \begin{pmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \\ \end{pmatrix} [/math]
Wie man sieht, können die Einträge im Kern durchaus auch negativ sein. Soweit, so gut. Wir haben also unsere beiden Operanden, das Bild und den Kern. Nun müssen wir nur noch wissen, was wir mit denen machen sollen. Irgendwie müssen wir beide miteinander verrechnen, um ein Ergebnisbild zu erhalten.
Wir machen folgendes: Wir packen uns den Faltungskern in Gedanken in der Mitte (an der 4) und schieben ihn Pixel für Pixel über das Bild. Wir multiplizieren jetzt die übereinander liegenden Werte von Bild und Kern miteinander und Addieren die Produkte auf. Das Ergebnis ist der neue Wert für das Pixel, über dem die Mitte des Kerns gerade liegt.
Nich kapiert? Macht nix, hier mal ein Bild. Wir haben den Kern also soweit geschoben, dass die Mitte (die 4) genau über der 0 in der zweiten Zeile, zweite Spalte des Bildausschnittes liegt.
[math] \begin{pmatrix} \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots \\ \dots & 20 _0 & 20 _{-1} & 20 _0 & 100 & 100 & 100 & \dots \\ \dots & 20 _{-1} & 20 _4 & 20 _{-1} & 100 & 100 & 100 & \dots \\ \dots & 20 _0 & 20 _{-1} & 20 _0 & 100 & 100 & 100 & \dots \\ \dots & 20 & 20 & 20 & 100 & 100 & 100 & \dots \\ \dots & 20 & 20 & 20 & 100 & 100 & 100 & \dots \\ \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots & \vdots \\ \end{pmatrix} [/math]
Ich habe die Zahlen des Kerns klein hinter die Pixelwerte geschrieben. Jetzt Multiplizieren wir also die Pixelwerte mit den dazugehörigen Zahlen aus dem Kern und Addieren die einzelnen Produkte auf.
Also los gehts: [math] 20 \cdot 0 + 20 \cdot -1 + 20 \cdot 0 + 20 \cdot -1 + 20 \cdot 4 + 20 \cdot -1 + 20 \cdot 0 + 20 \cdot -1 + 20 \cdot 0 = 0 [/math] Na so eine Überraschung. Der neue Wert für den Pixel, an dem jetzt die 4 vom Kern stand, ist also 0. Machen wir also ins Ergebnisbild an die entsprechende Stelle einen komplett schwarzen Pixel.
Offensichtlich sind wir hier auf eine interessante Eigenschaft dieses Faltungskernes gestoßen: Liegt er über einer gleichfarbigen Fläche, ist das Ergebnis der Rechnung 0 ... genau das, was wir für eine Kantenerkennung brauchen, oder? Jetzt ist nur noch die Frage, was passiert, wenn der Kern über einer Kante liegt? Rechnet doch selber mal nach. Schiebt also den Kern Pixel für Pixel über das alte Bild und rechnet nach der obigen Anleitung die Farbwerte für das neue Bild aus. Wer richtig gerechnet hat, erhält folgendes Ergebnisbild:
[math] \begin{pmatrix} \vdots & \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots \\ \dots & 0 & 0 & -80 & 80 & 0 & 0 & \dots \\ \dots & 0 & 0 & -80 & 80 & 0 & 0 & \dots \\ \dots & 0 & 0 & -80 & 80 & 0 & 0 & \dots \\ \dots & 0 & 0 & -80 & 80 & 0 & 0 & \dots \\ \dots & 0 & 0 & -80 & 80 & 0 & 0 & \dots \\ \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots & \vdots \\ \end{pmatrix} [/math]
Anstelle von -80 schreiben wir einfach +80 in das Bild, das ist kein Problem. So, was ist hier passiert? Offensichtlich haben wir mit dieser einfachen Rechnung unsere Kante genau markiert. Dort, wo vorher der Übergang von 20 auf 100 war, befinden sich jetzt zwei Spalten mit dem Farbwert 80. Herzlichen Glückwunsch zur Kantenerkennung!
|
Sei [math]I_{(x,y)}[/math] unser Bild und [math]K_{(u,v)}[/math] unser Faltungskern. Dann definieren wir das Ergebnis der linearen Faltung mit Kern [math]K[/math] als:
|
Dieser Faltungskern, der so schön die Kanten im Bild markiert, hat natürlich auch einen Namen. Das ist nämlich der Laplace-Operator.
Wie kommen eigentlich diese Zahlen im Kern, also die -1 und die 4 und ihre symetrische Anordnung zustande? Auf eine genaue Herleitung möchte ich an dieser Stelle verzichten. Das hat was mit partiellen Ableitungen zu tun. Wer irgendwann mal studiert, wird sich damit noch früh genug plagen dürfen, solange sollt ihr verschont bleiben.
Tabelle der Faltungskerne
| Faltungskern | Beschreibung |
|---|---|
| [math] \frac{1}{9} \begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\ \end{pmatrix} [/math] | Unschärfeoperator, glättet Kanten im Bild |
| [math] \begin{pmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \\ \end{pmatrix} [/math] | horizontaler Sobel-Operator, hebt waagerechte Kanten hervor |
| [math] \begin{pmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \\ \end{pmatrix} [/math] | vertikaler Sobel-Operator, hebt senkrechte Kanten hervor |
| [math] \begin{pmatrix} 1 & 1 & 1 \\ -1 & -2 & 1 \\ -1 & -1 & 1 \\ \end{pmatrix} [/math] | hebt Kanten in Nordostrichtung (schräg rechts nach oben) hervor |
| [math] \begin{pmatrix} -1 & -1 & 1 \\ -1 & -2 & 1 \\ 1 & 1 & 1 \\ \end{pmatrix} [/math] | hebt Kanten in Südostrichtung (schräg rechts nach unten) hervor |
weitere Anwendungen der linearen Faltung
Im letzten Abschnitt haben wir den Laplace-Operator kennengelernt und das Prinzip der Linearen Faltung verstanden. Natürlich gibt es noch eine Vielzahl weiterer Faltungskerne, von denen jeder interessante Eigenschaften hat. Tabelle 2.1 fasst einige davon zusammen.
Anmerkung: Die [math]\frac{1}{9}[/math] vor dem Kern bedeutet einfach, dass mal alle Zahlen im Kern mit [math]\frac{1}{9}[/math] multiplizieren muß.
Die Anwendung der beiden Sobeloperatoren für die horizontalen und vertikale Kanten erlaubt uns noch eine weitere Information zu berechnen: Wenn wir zuerst den einen und dann den anderen Operator auf das Originalbild anwenden, erhalten wir zwei Ergebnisbilder, ich nenne die mal [math]B_x[/math] und [math]B_y[/math]. Um beide zu kombinieren können wir einfach den Mittelwert [math]\frac{B_{x(P)} + B_{y(P)}}{2}[/math] für jeden Pixel P bilden, oder wir rechnen mathematisch exakt (aber aufwändiger) [math]\sqrt{B_{x(P)} ^2 + B_{y(P)} ^2}[/math]. Sieht aus wie die Formel vom Satz des Pythagoras, oder?
Das eigentlich Interessante ist aber, dass wir hier ganz einfach für jeden Pixel die Richtung der Kante bestimmen können: [math]\mathrm{Kantenrichtung} = \operatorname{atan}\,\left ( \frac{B_{y(P)}}{B_{x(P)}} \right )[/math].
Erinnert ihr euch noch an Bild 1.1? Wir hatten es im ersten Kapitel in den HSV-Farbraum umgerechnet.
Abbildung 2.1 zeigt die Szene nach Anwendung des kombinierten Sobel-Operators (horizontal+vertikal).