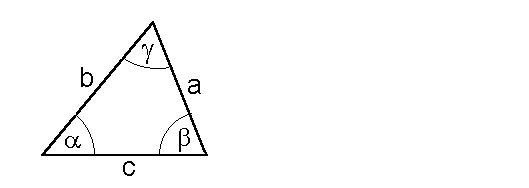Inhaltsverzeichnis
Einleitung
Dieser Beitrag dient dem groben Verständniss der Technischen Mechanik. Natürlich kann ich hier nur einen kleinen Ausschnitt zeigen, da das Thema einfach zu umfassend ist.
Ich werde das Prinzip der Technischen Mechanik sowie alle Berechnungen anhand des Beispiels eines Hexapod´s erläutern.
Am Ende dieses Beitrags solltet Ihr in der Lage sein folgende Berechnungen durchzuführen:
- Kräfte und Momente am Lager berechnen.
- Spannungen im Bauteil berechnen.
- Aussagen über die Sicherheit gegen Bruch/Versagen treffen.
- Verformung und Festigkeit berechnen.
Was ist Technische Mechanik?
Die Technische Mechanik betrachtet Zustände von Körpern unter Einfluss von Kräften und Momenten.
Dabei unterscheidet man zwischen:
1)Statik: Die Mechanik der starren Körper.
2)Elastomechanik/Elastostatik: Die Mechanik der deformierbaren Körper.
3)Kinetik/Kinematik: Die Mechanik der dynamischen Systeme. [math]\Leftarrow[/math] Auf Kinetik werde ich hier nicht näher eingehen.
Statik
Die Statik befasst sich mit dem Gleichgewicht der Kräfte/Momente am ruhenden Körper. Mit der Statik lassen sich Lagerkräfte bzw. resultierende Kräfte berechnen. Allerdings berücksichtigt die Statik weder das Material, noch die Geometrie des Querschnitts. Somit lässt sich mit der Statik keine Aussage über die Belastungen des Bauteils selbst treffen.
Verdeutlichen wir das einmal durch folgendes Beispiel:
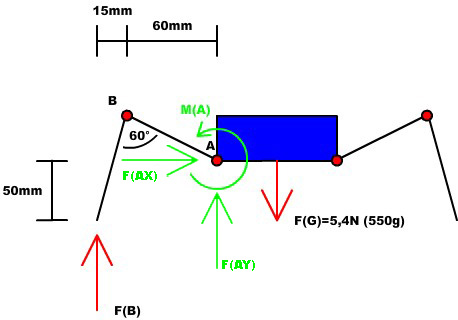
Wir wollen berechnen welche/s Kraft/Moment auf den Schulterservo allein durch das Gewicht des Hexapod wirkt.
Dazu müssen wir erstmal ein mechanisches Ersatzmodell (Skizze) Bilden:
Die Gewichtskraft [math]F_G[/math] resultiert aus dem Gewicht (in Kg) multipliziert mit der Erdbeschleunigung [math]g=9,81 m/s^2[/math],
denn: [math]F=m\cdot a[/math] , also Kraft = Masse * Beschleunigung.
Nun müssen wir die Gleichgewichtsbedingungen aufstellen: (Also die Summe aller Kräfte in x/y Richtung und des Momentes um den Punkt A = 0)
(1)[math]\Sigma\vec x =: 0[/math]
(2)[math]\Sigma\uparrow y =: F_B - F_G = 0[/math]
(3)[math]\Sigma M_A =: F\cdot (15mm + 60mm) - M_A = 0[/math]
Aus (2) erhalten wir: [math]F_B = F_G[/math]
da wir davon ausgehen das die Spinne immer mit mindestens 3 Beinen auf dem Boden steht rechnen wir mit der Ersatzkraft: [math]F = \frac{1}{3}F_B = \frac{1}{3}F_G = 1.8N[/math]
Setzen wir nun die Ersatzkraft F, die wir aus (2) berechnet haben, in (3) ein, erhalten wir:
[math]M_A = F \cdot (15mm + 60mm) \Rightarrow M_A = 135N/mm = 13.5N/cm[/math]
Der Schulterservo muss also mindestens 13.5N/cm haben.
Mit einem Sicherheitsfaktor von 1.5 Multipliziert erhalten wir: [math]13.5N/cm \cdot 1.5 \approx 20N/cm[/math]
Elastomechanik
Für weitere Berechnungen, wie Verformung und Spannungen im Material etc. braucht man nun die Elastomechanik. Die Elastomechanik befasst sich mit der Berechnung der Verformung und Festigkeit und ermöglicht Aussagen über die Sicherheit gegen Versagen und Bruch.
Verdeutlichen wir dass wieder am Beispiel des Hexapod:
Wenn der Hexapod läuft bewegt er sich ja nicht "flüssig" wie ein Roboter mit Rädern, sondern "ruckartig".
Wir gehen hier mal von einer 3:3 Schrittfolge aus, Infos zu Schrittfolgen hier: Spinnenbeine (Hexapods).
Jetzt sind 2 Fälle denkbar:
Der Hexapod steht mit drei Beinen auf dem Boden und bewegt sich über diese nach vorne:
1)Bevor er jetzt mit den angehobenen Beinen wieder auftritt muss er zum Stillstand kommen.
2)Der Hexapod tritt mit den 3 angehobenen Beinen noch in der Bewegung auf und kommt plötzlich zum Stillstand.
Variante 2 würde ich bevorzugen, da so eine schnellere Fortbewegung möglich ist.
In beiden Fällen müssen 3 Beine die Querkräfte aufnehmen, in Fall 2 treten aber wesentlich höhere Querkräfte auf, da das Abbremsen über einen kürzeren Zeitraum geschieht.
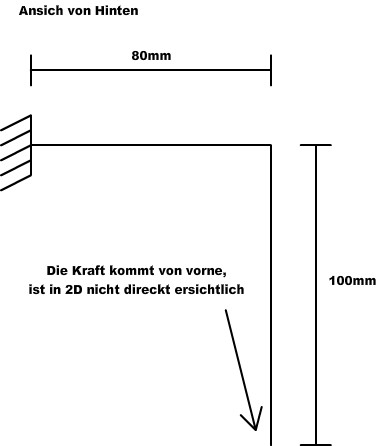
Hier eine Skizze zur Verdeutlichung:
Was ist das gefährliche an Querkräften?
-Die Querkraft greift über einen dünneren Querschnitt an (dazu später mehr)
-Die Querkraft sorgt für eine Torsion des Oberschenkels (dazu später mehr)
Physik Exkurs
Wir müssen nun berechnen wie hoch diese Querkräfte sind, dazu brauchen wir etwas Physik!
Die Kraft in Querrichtung hängt von der Beschleunigung ab, die die Spinne beim Auftreten negativ und Losgehen positiv erfährt.
Die höhere von Beiden ist logischerweise die beim Auftreten, denn sie ist "ruckartiger", also in einem kurzerem Zeitraum. Deshalb kann man die Beschleunigung und die daraus resultierende Querkraft beim Losgehen ignorieren.
[math]F=m\cdot a[/math] , Kraft = Masse * Beschleunigung
[math]a = \frac{\Delta v(t)}{\Delta t}[/math] , Beschleunigung = Geschwindigkeitsunterschied pro Zeitraum
Die Beschleunigung hängt von der Geschwindigkeit ab. Die Geschwindigkeit wird wiederrum von der Schrittweite und der Geschwindigkeit der Servos definiert, denn:
[math]V = \frac{s}{t}[/math] , Geschwindigkeit = Weg / Zeit
Um diesen Gedankengang zu verdeutlichen:
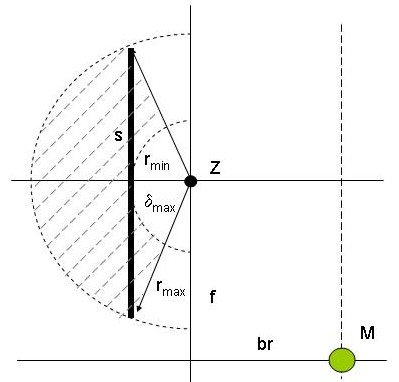
Die Schrittweite bzw. der Weg S hängt vom Radius [math]r_{max}[/math] und dem Winkel [math]\delta_{max}[/math] ab.
Der Winkel [math]\delta_{max}[/math] bildet sich zwischen den beiden Pfeilen [math]r_{max}[/math], somit ergibt sich mit Schrittweite S ein gleichschenkliges Dreieck.
Im Beispielsfall beträgt [math]r_{max} = 80mm[/math] und [math]\delta_{max} = 30°[/math].
Verwendet man nun den Cosinussatz:
[math]c^2 = a^2 + b^2 - 2ab * \cos \gamma[/math]
Und setzt die Werte ein, erhält man:
[math]s = \sqrt{r_{max}^2 + r_{max}^2 - 2r_{max}r_{max} * \cos \delta _{max}}[/math] [math]\Rightarrow[/math] [math]s \approx 40mm[/math]
Als Servo Geschwindigkeit hab ich in diesem Fall 0.2s/60° gefunden. Und die Schrittweite hab ich aus dem max. möglichen Drehwinkel des Schulterservos (30°) sowie dem Abstand von Servo Achse zur Auftrittsfläche (80mm) ermittelt, sie beträgt bei mir etwa 40mm.
Somit haben wir: [math]V = 40mm/0.1s[/math]
Jetzt müssen wir aber auch noch anheben und absenken des Beines dazu rechnen, da es ja nicht komplett simultan zur Drehbewegung geschiet, denn das Bein muss erst leicht angehoben sein um es zu drehen.
Also nehmen wir einfach mal: [math]V = 40mm/0.15s[/math].
Die Servogeschwindigkeit wird wohl nicht erreicht werden, aber das ist egal, denn so würde die Belastung ja nur kleiner werden!!!
Rein Theoretisch müsste die Spinne also etwa folgende Geschwindigkeit erreichen:
[math]V = 40mm/0.15s = 0.96km/h[/math]
Wie wir oben schon gesehen haben verteilt sich die Querkraft auf 3 Beine.
Die Beschleunigung tritt nun also immer dann ein, wenn die Spinne auftritt und somit von 0.267m/s auf 0m/s gebremst wird. Bzw. beim losgehen von 0m/s auf 0.267m/s beschleunigt. Das ist ja die Zeit, in der die Spinne das bein anhebt oder senkt, also 0.05s.
Nun kann man über Impuls (p = m * v = 0.14685 kg*m/s) oder Beschleunigung (a = dv(t)/dt = 5.34m/s^2) rechnen, ich nehme Impuls, bins halt so gewohnt...
F = p/dt = 0.14685 Kg*m/s / 0.05s = 2.937N
Da die Kraft aber auf 3 Beine Wirkt sind es etwa 1 N pro bein!