Inhaltsverzeichnis
Einleitung
Dieser Beitrag dient dem groben Verständnis der Technischen Mechanik. Natürlich kann ich hier nur einen kleinen Ausschnitt zeigen, da das Thema einfach zu umfangreich ist.
Ich werde das Prinzip der Technischen Mechanik sowie alle Berechnungen anhand des Beispiels eines Hexapods erläutern.
Am Ende dieses Beitrags solltet ihr in der Lage sein folgende Berechnungen für eigene Projekte durchzuführen:
- Kräfte und Momente am Lager berechnen.
- Spannungen im Bauteil berechnen.
- Verformung (Biegung/Torsion) und Festigkeit berechnen.
- Aussagen über die Sicherheit gegen Bruch/Versagen treffen.
- Bauteildimensionierung.
Was ist Technische Mechanik?
Die Technische Mechanik ist ein Spezialgebiet der Physik und betrachtet Zustände von Körpern unter Einfluss von Kräften und Momenten.
Dabei unterscheidet man zwischen:
1) Statik: Die Mechanik der starren Körper in Ruhe. Gehört zur Starrkörperphysik, ist aber eine Art "Wissenschaft für sich"
2) Elastomechanik, auch: Festigkeitslehre: Die Mechanik der deformierbaren Körper. Eigentlich gehören auch Flüssigkeiten und Gase dazu, aber die werden gesondert behandelt (Fluidmechanik, Thermodynamik).
3) Kinematik: Betrachtung von Bewegungen eines "Punktes", geradlinig, auf einer Kreisbahn oder beides gleichzeitig
4) Dynamik:: Jetzt bekommt der sich bewegende Punkt eine Masse ("Massenpunkt") und damit auch Impuls, Kräfte/Momente und Bewegungs- und Lageenergie.
5) Starrkörperphysik: Auf Körper mit Masse und Volumen (angenommen als homogen und unverformbar) werden Kinematik, Statik und Dynamik angewendet. Bei einer Drehbewegung kommt jetzt z.B. das Trägheitsmoment ins Spiel.
6) Schwingungslehre (Schwingung: perodische Zustandsänderung eines Systems um einen Gleichgewichtszustand)
7) Werkstoffkunde: Die Chemie der Werkstoffe. Hier kommen die Kennwerte her, mit denen die Festigkeitslehre arbeitet.
Man betrachtet (um die Verwirrung perfekt zu machen) zweidimensionale (ebene) und dreidimensionale (räumliche) Systeme. Wo auch immer möglich versucht man, zweidimensionale Rechnungen anzuwenden, denn: Bei räumlichen Systemen kommt man leider häufig nicht um Matrizenrechnung herum.
Wo und wie lerne ich mehr darüber?
Zum Verständnis mechanischer Berechnungen werden sichere mathematische Kenntnisse in den Bereichen Geometrie, Vektorrechnung und Analysis benötigt.
Wer (teure) Fachliteratur, Formeln und Tabellen sucht, wird in der Stadtbücherei fündig. Außerdem geben Firmen wie z.B. INA (Wälzlager) kleine Tabellenbücher auch als Werbegeschenke raus.
Bei Interesse an diesem Themengebiet (und entsprechender Befähigung) ist schulische Bildung in Form des Physik-Leistungskurses (Sekundarstufe II) dem Verständnis sehr zuträglich. Es sei an dieser Stelle noch erwähnt, dass die technische Mechanik (und zwar mit allen Details) der Hauptinhalt (und neben Thermodynamik der trockenste Stoff) des Maschinenbaustudiums an einer Uni oder FH ist.
Statik
Die Statik befasst sich mit dem Gleichgewicht der Kräfte/Momente am ruhenden Körper. Mit der Statik lassen sich Lagerkräfte bzw. resultierende Kräfte berechnen. Allerdings berücksichtigt die Statik weder das Material, noch die Geometrie des Querschnitts. Somit lässt sich mit der Statik keine Aussage über die Belastungen des Bauteils selbst treffen.
Verdeutlichen wir das einmal durch folgendes Beispiel:
Wir wollen berechnen welche/s Kraft/Moment auf den Schulterservo allein durch das Gewicht des Hexapod wirkt.
Damit eine Kraft auf einen Balken (Werkstück) wirken kann muss es gelagert (befestigt) sein, sonst würde man es ja wegschieben.
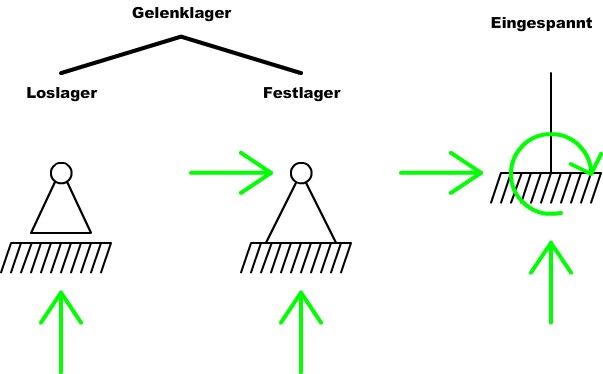
Dabei gibt es verschiedene Arten etwas zu lagern:
Loslager: Das Loslager, ein Gleitlager, kann in dieser Anordnung nur Kräfte in Y-Richtung aufnehmen.
Festlager: Das Festlager kann sowohl Kräfte in Y- als auch X-Richtung aufnehmen.
Eingespannt: Bei einer Einspannung wird zu den Kräften in X/Y-Richtung auch noch ein Moment aufgenommen.
Bei unseren Servos handelt es sich um eine Einspannung, da sie ja das Moment aufnehmen müssen, damit die Spinne stehen bleibt.
Hexapod
Wir müssen erstmal ein mechanisches Ersatzmodell (Skizze) bilden:
| Dieser Artikel ist noch lange nicht vollständig. Der Auto/Initiator hofft das sich weitere User am Ausbau des Artikels beteiligen.
Das Ergänzen ist also ausdrücklich gewünscht! Besonders folgende Dinge würden noch fehlen: Dieser Absatz war stark fehlerbehaftet und wird z.Zt. überarbeitet --Max2k 03:41, 16. Mär 2008 (CET) |
Zunächst einmal legen wir ein rechtwinkliges Koordinatensystem fest und zeichnen es in die Skizze ein [math]\uparrow[/math] y-Richtung [math]\rightarrow[/math] x-Richtung
Die Gewichtskraft [math]F_G[/math] resultiert aus dem Gewicht (in kg) multipliziert mit der Erdbeschleunigung [math]g=9,81 m/s^2[/math],
denn: [math]F=m\cdot a[/math] , also Kraft = Masse * Beschleunigung.
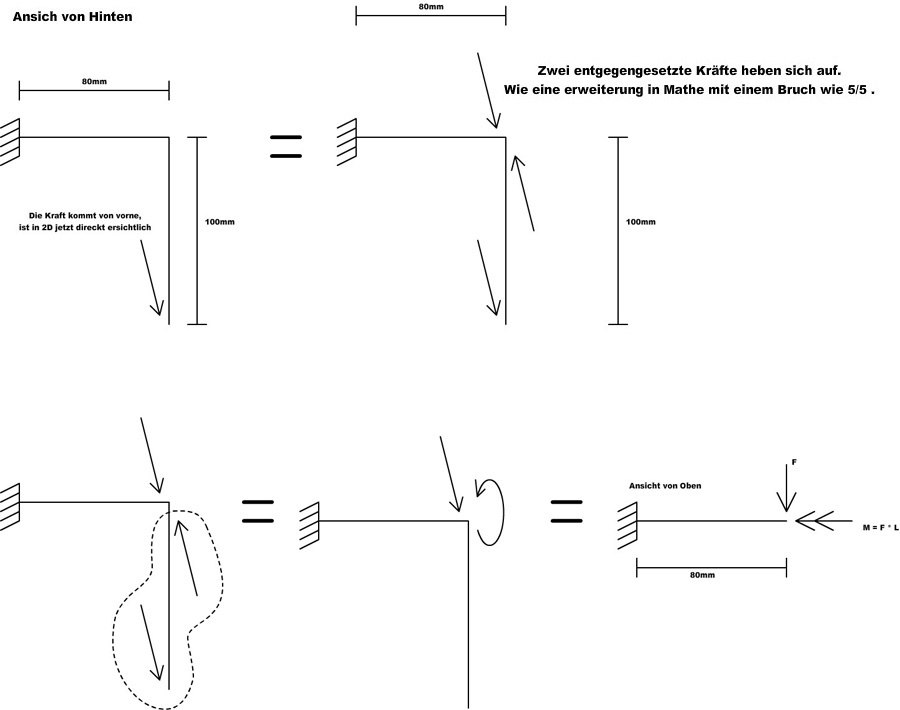
Als nächstes folgt das sogenannte Freischneiden des Systems. Man darf dazu Teile des Systems wegschneiden und stattdessen die an der Schnittstelle wirkenden Kräfte antragen
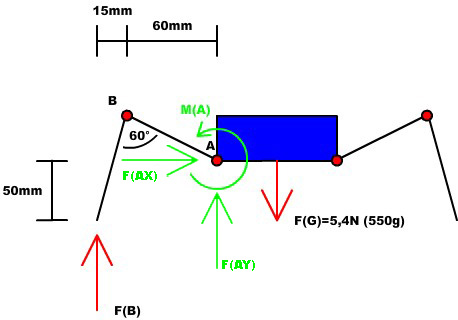
Wir betrachten zunächst einmal nur ein Bein des Bots und die Achse des Servos, Punkt A.
Wir dürfen für das Kräftegleichgewicht[math]F_G[/math] vom Körperschwerpunkt parallel in den Punkt A (Servo) verschieben. F_G wirkt auf alle Beine. Für ein einzelnes Bein fließt F_G in die Körperkräfte in y-Richtung mit ein (wie genau hängt noch von anderen Bedingungen ab, dazu gleich mehr)
Wir müssen Lagerkräfte F_AX und F_AY antragen, und außerdem Körperkräfte, die den Punkt A an Ort und Stelle im Gleichgewicht halten.
Jetzt haben wir das Bein vom Körper freigeschnitten. Von der Beinkraft wissen wir noch nicht, in welche Richtung sie wirkt, also zerlegen wir sie in eine x- und eine y-Komponente.
Nun müssen wir die Gleichgewichtsbedingungen aufstellen: (Also die Summe aller Kräfte in x/y-Richtung und der Momente um den Punkt A = 0)
(1)Summe der Kräfte in x-Richtung = 0: F_(A,x)+F_(Körper,x) +F_(B,x)=0
(2)Summe der Kräfte in y-Richtung = 0: F_(A,y)+F_(Körper,y) +F_(B, y) - F_G = 0
(3)Summe der Momente im Punkt A= 0: M_Körper - F_(B,x) * 0,075m + F_(B,y) * 0,05m
Nun sehen wir, dass wir zu viele Unbekannte haben, um die Gleichungen auflösen zu können.
Das bedeutet: Zusätzliche Informationen sammeln bzw. zusätzliche Gleichungen aufstellen.
In jedem einzelnen Fall müssen wir die Kräfte und Momente im Körper bestimmen. Diese sind abhängig von:
- der Anzahl der Beine, die den Boden berühren (Kräftegleichungen)
- der Position am Körper der Beine, die den Boden berühren
Die Kräfte F_Bein,x und F_Bein,y können wir als Funktion von Anstellwinkel und F_Bein ausdrücken:
(5) F_B,y = F_B * sin(alpha)
(6) F_B,x = F_B * cos(alpha)
alpha ist der Winkel zwischen: der Geraden zwischen Auflagepunkt des Beinendes und Punkt A und der Ebene "Boden". Der Kraftvektor F_Bein zeigt entlang dieser Geraden.
Stillstand:
Wir machen noch eine zusätzliche Annahme: In x-Richtung können die Füße des Bots keine Kräfte an den Boden übertragen, es gilt:
(7)F_B,x=0
Man kann sich das so vorstellen: Selbst wenn der Bot auf einer glatten Oberfläche (Eis) steht, darf er keine "Grätsche" machen. Für das Moment gilt (7) in (3).
Alter Text
somit gilt: [math]F_G = F_{AY}[/math] Aus (2) erhalten wir: [math]F_B = F_G[/math]
da wir davon ausgehen, dass die Spinne immer mit mindestens 3 Beinen auf dem Boden steht, rechnen wir mit der Ersatzkraft: [math]F = \frac{1}{3}F_B = \frac{1}{3}F_G = 1.8N[/math]
Setzen wir nun die Ersatzkraft F, die wir aus (2) berechnet haben, in (3) ein, erhalten wir:
[math]M_A = F \cdot (15mm + 60mm) \Rightarrow M_A = 135N/mm = 13.5N/cm[/math]
Der Schulterservo muss also mindestens 13.5N/cm haben.
Mit einem Sicherheitsfaktor von 1.5 multipliziert erhalten wir: [math]13.5N/cm \cdot 1.5 \approx 20N/cm[/math]
Elastomechanik Modellfindung
Für weitere Berechnungen, wie Verformung und Spannungen im Material etc. braucht man nun die Elastomechanik. Die Elastomechanik befasst sich mit der Berechnung der Verformung und Festigkeit und ermöglicht Aussagen über die Sicherheit gegen Versagen und Bruch.
Verdeutlichen wir das wieder am Beispiel des Hexapod:
Wenn der Hexapod läuft bewegt er sich ja nicht "flüssig" wie ein Roboter mit Rädern, sondern "ruckartig".
Wir gehen hier mal von einer 3:3 Schrittfolge aus, Infos zu Schrittfolgen hier: Spinnenbeine (Hexapods).
Jetzt sind 2 Fälle denkbar:
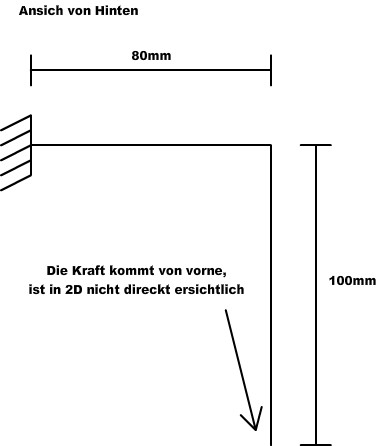
Der Hexapod steht mit drei Beinen auf dem Boden und bewegt sich über diese nach vorne:
1)Bevor er jetzt mit den angehobenen Beinen wieder auftritt muss er zum Stillstand kommen.
2)Der Hexapod tritt mit den 3 angehobenen Beinen noch in der Bewegung auf und kommt plötzlich zum Stillstand.
Variante 2 würde ich bevorzugen, da so eine schnellere Fortbewegung möglich ist.
In beiden Fällen müssen 3 Beine die Querkräfte aufnehmen, in Fall 2 treten aber wesentlich höhere Querkräfte auf, da das Abbremsen über einen kürzeren Zeitraum geschieht.
Hier eine Skizze zur Verdeutlichung:
Was ist das Gefährliche an Querkräften?
- Die Querkraft greift über einen dünneren Querschnitt an (dazu später mehr)
- Die Querkraft sorgt für eine Torsion des Oberschenkels (dazu später mehr)
Physik-Exkurs
Wir müssen nun berechnen wie hoch diese Querkräfte sind, dazu brauchen wir etwas Physik!
Die Kraft in Querrichtung hängt von der Beschleunigung ab, die die Spinne beim Auftreten negativ und Losgehen positiv erfährt.
Die höhere von beiden ist logischerweise die beim Auftreten, denn sie ist "ruckartiger", also in einem kürzerem Zeitraum. Deshalb kann man die Beschleunigung und die daraus resultierende Querkraft beim Losgehen ignorieren.
[math]F=m\cdot a[/math] , Kraft = Masse * Beschleunigung
[math]a = \frac{\Delta v(t)}{\Delta t}[/math] , Beschleunigung = Geschwindigkeitsunterschied pro Zeitraum
Die Beschleunigung hängt von der Geschwindigkeit ab. Die Geschwindigkeit wird wiederum von der Schrittweite und der Geschwindigkeit der Servos definiert, denn:
[math]V = \frac{s}{t}[/math] , Geschwindigkeit = Weg / Zeit
Um diesen Gedankengang zu verdeutlichen:
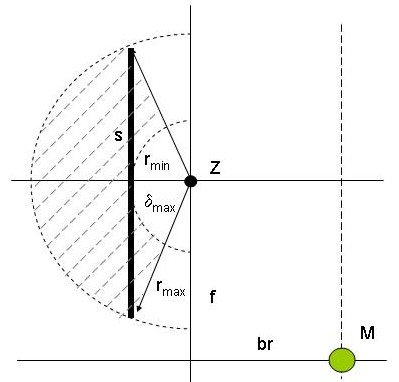
Die Schrittweite bzw. der Weg S hängt vom Radius [math]r_{max}[/math] und dem Winkel [math]\delta_{max}[/math] ab.
Der Winkel [math]\delta_{max}[/math] bildet sich zwischen den beiden Pfeilen [math]r_{max}[/math], somit ergibt sich mit Schrittweite S ein gleichschenkeliges Dreieck.
Im Beispielsfall beträgt [math]r_{max} = 80mm[/math] und [math]\delta_{max} = 30[/math]°.
Verwendet man nun den Cosinussatz
[math]c^2 = a^2 + b^2 - 2ab * \cos \gamma[/math]
und setzt die Werte ein, erhält man:
[math]s = \sqrt{r_{max}^2 + r_{max}^2 - 2r_{max}r_{max} * \cos \delta _{max}}[/math] [math]\Rightarrow[/math] [math]s \approx 40mm[/math]
Als Servo-Geschwindigkeit hab ich in diesem Fall 0.2s/60° gefunden.
Somit haben wir: [math]V = 40mm/0.1s[/math]
Jetzt müssen wir aber auch noch Anheben und Absenken des Beines dazu rechnen, da es ja nicht komplett simultan zur Drehbewegung geschieht, denn das Bein muss erst leicht angehoben sein, um es zu drehen.
Also nehmen wir einfach mal: [math]V = 40mm/0.15s[/math].
Die Servogeschwindigkeit wird wohl nicht erreicht werden, aber das ist egal, denn so würde die Belastung ja nur kleiner werden!!!
Rein theoretisch müsste die Spinne also etwa folgende Geschwindigkeit erreichen:
[math]V = 40mm/0.15s = 0.96km/h[/math]
Die Beschleunigung tritt nun also immer dann ein, wenn die Spinne auftritt und somit von 0.267m/s auf 0m/s gebremst wird.
Der Zeitraum, in dem die negative Beschleunigung auftritt, ist die Zeit in der die Spinne das Bein anhebt oder senkt, also 0.05s.
Nun kann man über den Impulssatz: [math]p = m * v = 0.14685 \frac{kg \cdot m}{s}[/math] oder die Beschleunigung [math]a = \frac{\Delta v(t)}{\Delta t} = 5.34m/s^2[/math] rechnen,
ich nehme den Impuls, bin's halt so gewöhnt ...
[math]F = \frac{p}{\Delta t} = \frac{0.14685 Kg \cdot m/s}{0.05s} = 2.937N[/math]
Wie wir oben schon gesehen haben verteilt sich die Querkraft auf 3 Beine [math]\Rightarrow[/math] 1 N pro bein!
Elastomechanik - Die Berechnungen
Damit beenden wir den Physik-Exkurs und kommen zurück zur Elastomechanik. Da wir nun die Querkräfte berechnet haben, die auf ein Bein wirken, haben wir nun fast alle Daten, die wir zur Berechnung der Verformung und Belastung benötigen.
Was fehlt nun noch?
Wir müssen festlegen, aus welchem Material wir die Teile fertigen, denn Stahl ist z.B. stabiler als Lexan (Polycarbonat) und wird sich auch weniger verformen.
Außerdem müssen wir uns noch auf einen Querschnitt, also die Dimensionierung der Beine einigen, was auch einen erheblichen Einfluss auf Belastbarkeit und Verformung hat.
Materialkennwerte
Jedes Material hat andere Eigenschaften. Das eine ist sehr hart und damit mit sehr hohen Kräften belastbar, dadurch aber fast nicht verformbar und bricht bei Überlastung sofort. Das andere Material ist zäh und kann sich leicht elastisch verformen ohne zu brechen.
Diese Materialkennwerte findet man in Tabellen und im Internet.
Zug / Druck
Die Eigenschaften eines Werkstoffes unter Zug/Druck spiegeln sich in folgenden Werten wider:
E - Das Elastizitätsmodul
[math]\sigma _{zul}[/math] - Die zulässige Spannung.
Das E-Modul hat folgenden Zusammenhang:
[math]E = \frac{\sigma}{\epsilon}[/math]
[math]\epsilon = \frac{\Delta l}{l_0}[/math] , die Dehnung.
Ist die Ausgangslänge [math]l_0 = 100mm[/math] und die Länge nach Einwirkung einer Kraft [math]l_1 = 110mm[/math], dann ist die Längendifferenz [math]\Delta l = 10mm[/math]. Daraus folgt: [math]\epsilon = \frac{10mm}{100mm} = 0.1 = 10%[/math]
[math]\sigma = \frac{F}{A}[/math] , Spannung = Kraft pro Fläche (Querschnittfläche)
Das Elastizitätsmodul eines Materials ist die Spannung, bei der sich das Werkstück in seiner Länge verdoppeln würde.
Je mehr Widerstand ein Material seiner Verformung entgegensetzt, umso höher ist das E-Modul.
Stahl hat somit ein sehr hohes E-Modul und Gummi z.B. ein sehr kleines.
[math]\sigma _{zul}[/math] - Die zulässige Spannung ist ein in Versuchen ermittelter Wert, der angibt, welche Spannungen, also Kraft pro Fläche, das Material in Zug- und Druckrichtung verträgt.
Schubspannungen (Torsion)
Verdrehen/torieren wir ein Werkstück wie ein Handtuch, das wir auswringen, treten Schubspannungen auf. Das ist später bei dem Oberschenkel der Fall, durch den Hebel des Unterschenkels verdrehen wir den Oberschenkel. Schubspannungen sind dabei die kritischsten, sie treten auf, wenn sich das Material an einer Stelle in entgegengesetzte Richtungen verformt und sich somit abschert, alle Materialien sind sehr anfällig gegen Schubspannungen.
Die Eigenschaften eines Werkstoffes unter Schubspannung spiegeln sich in folgenden Werten wider:
G - Das Schubmodul, equivalent zum E-Modul.
[math]G = \frac{\tau}{\gamma}[/math]
[math]\tau[/math]: Die Schubspannung
[math]\gamma[/math]: Der Scherwinkel
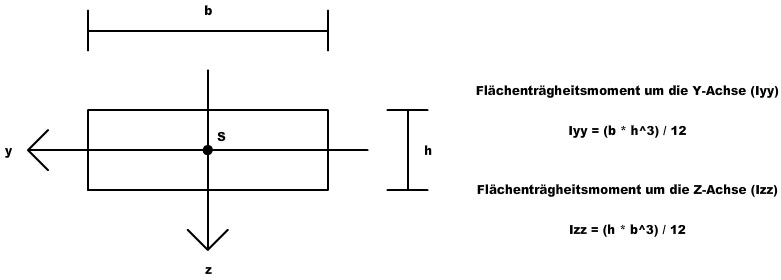
Flächenträgheitsmoment
Trägheit bedeutet das "Bestreben" des Körpers in seinem Bewegungszustand zu verharren. Je höher die träge Masse eines Körpers ist, umso weniger verändert eine auf ihn einwirkende Kraft seinen Bewegungszustand.
Das Flächenträgheitsmoment ist equivalent dazu das "Bestreben" eines Körpers sich einer Biegung zu widersetzen. Somit ist das Flächenträgheitsmoment ein Maß für die Steifigkeit eines Querschnittes gegen Biegung.
Ein ganz einfaches Beispiel:
Ihr nehmt ein Lineal und biegt es über den schmalen Querschnitt ... kein Problem.
Versucht das gleiche jetzt mal hochkant.
Das Flächenträgheitsmoment berechnet sich je nach Geometrie des Querschnittes unterschiedlich, die Formeln hierzu finden sich in Tabellen und im Internet.
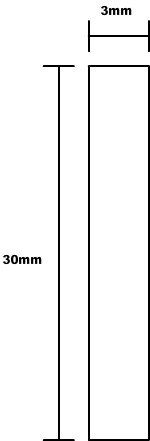
In unserem Beispiel des Hexapods ist der Querschnitt der Beine ein Rechteck:
Da die Achsen direkt im Schwerpunkt liegen, müssen wir den Schwerpunkt nicht weiter beachten. Wie mann anhand der Formeln sieht wird es wesentlich schwerer sein das Werkstück um die Z-Achse zu biegen, da Izz wesentlich größer als Iyy wird. Allerdings interessiert uns in unserem Fall nur Iyy.
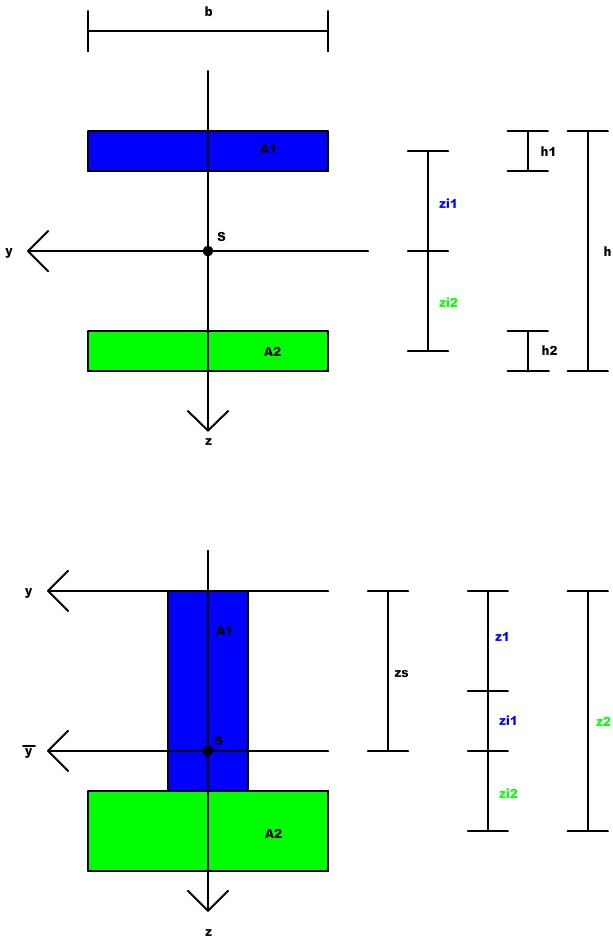
Bei aus mehreren Teilen zusammengesetzten Querschnitten, also z.B. T-Träger oder doppelt ausgelegte Oberschenkel eines Hexapod muss etwas umständlicher gerechnet werden.
Das ist für die Beispielsberechnung nicht weiter relevant, aber eventuell braucht ihr es mal selbst.
Oben ist die doppelte Auslegung eines Oberschenkels und unten ein T-Träger.
Wie man direkt erkennen kann hat der obere Fall einen Vorteil, wir wissen wo der Schwerpunkt S liegt, bei b/2 und h/2.
Des weiteren wissen wir auch, wo die Schwerpunkte der beiden einzelnen Teile liegen.
Das vereinfacht die Rechnung ein wenig, denn wir müssen nicht erst den Schwerpunkt bestimmen.
[math]I_{yys} = (I_{yy1} + z_{i1}^2 \cdot A_1) + (I_{yy2} + z_{i2}^2 \cdot A_2)[/math]
[math]I_{zzs} = I_{zz1} + I_{zz2}[/math]
Im unteren Fall wissen wir zwar auch, wo die Schwerpunkte der einzelnen Flächen liegen, aber nicht wo der Gesamtschwerpunkt liegt.
Aufgrund der Symmetrie können wir die Z-Achse direkt durch den Schwerpunkt legen, aber die Y-Achse müssen wir erstmal oben eintragen, denn wir wissen nicht, wo die Z-Koordinate des Schwerpunktes liegt.
Also müssen wir zuerst den Schwerpunkt berechnen:
[math]y_s = \frac{\Sigma y_i \cdot A_i}{\Sigma A_i} = 0[/math]
[math]z_s = \frac{\Sigma z_i \cdot A_i}{\Sigma A_i} = \frac{z_1 \cdot A_1 + z_2 \cdot A_2}{A_1 + A_2}[/math]
Wenn [math]z_s[/math] berechnet ist wissen wir wieder wie groß [math]z_{i1}[/math] und [math]z_{i2}[/math] ist und können wieder rechnen:
[math]I_{yys} = (I_{yy1} + z_{i1}^2 \cdot A_1) + (I_{yy2} + z_{i2}^2 \cdot A_2)[/math]
[math]I_{zzs} = I_{zz1} + I_{zz2}[/math]
Genug Theorie... Jetzt geht's los!
Da wir nun alle nötigen Werte und Grundkenntnisse haben können wir endlich mit der Berechnung der Verformungen und Spannungen anfangen.
Hier nochmal die Skizze:
Was passiert?
Der Unterschenkel wird von vorne mit der Kraft belastet und sich daher samt Oberschenkel nach hinten durchbiegen.
Zusätzlich überträgt der Unterschenkel als Hebel ein Torsionsmoment auf den Oberschenkel.
Aber eins nach dem anderen!
Verformung und Belastung des Unterschenkels
Als Material für alle Beine nehmen wir 3mm GFK (glasfaserverstärkter Kunststoff).
Die Materialkennwerte von GFK:
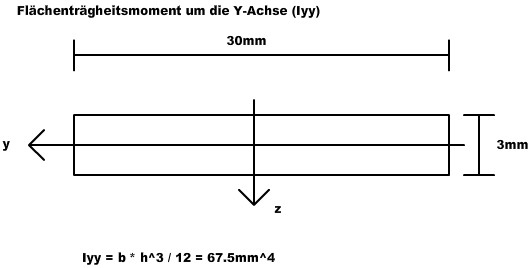
Das Flächenträgheitsmoment:
Da wir nun alle erforderlichen Werte bestimmt haben können wir die Durchbiegung am freien Ende berechnen:
Die maximale Durchbiegung am freien Ende ist [math]w_{max}[/math].
Um die Formel dazu nicht jedesmal herleiten zu müssen gibt es wieder ein Tabellenwerk:
Aus dem Tabellenwerk entnehmen wir:
[math]w_{max} = \frac{F \cdot l^3}{3 \cdot E \cdot I} = \frac{F \cdot 100^3}{3 \cdot E \cdot I_{yy}} = 0.11mm[/math]
Der Unterschenkel biegt sich also schon einmal um 0.11mm durch.
Jetzt berechnen wir die Spannung, die im Unterschenkel auftritt.
Dazu muss man schneiden, zur Erklärung:
Schneiden bedeutet man "zerschneidet" das Werkstück/den Balken, um die inneren Kräfte, die im Balken selbst wirken, freizulegen. Die Regel ist, man schneidet immer vor und nach einer Kraft bzw. Änderung. Eine Änderung kann hierbei ein Knick im Balken, ein Gelenk etc. sein.
Wie schon in der Statik müssen wir wieder die Gleichgewichtsbedingungen aufstellen.
Allerdings nur die des Momentes, da uns ja nur die Biegespannungen interessieren, die durch das Moment hervorgerufen werden, klarer wird das, wenn wir uns die Gleichung der maximalen Spannung anschauen:
[math]\sigma_{xx max}(x, z) = \frac{M_{y max}}{I_{yy}} \cdot z_{max}[/math]
Wie wir sehen spielt hier nur das maximale Moment eine Rolle. Das maximale Moment tritt logischerweise am Lager, also dem Servo auf, denn um so größer [math]x_1[/math] wird umso stärker wird das Moment:
[math]M_{y(max)} = M_{y(x1=100mm)} \Rightarrow M_{y(max)} = 1N * 100mm = 100N/mm[/math]
Setzen wir das maximale Moment nun in die Spannungsgleichung ein
[math]\sigma_{xx max}(x, z) = \frac{M_{y(max)}}{I_{yy}} \cdot z_{max} = \frac{100N/mm}{67.5mm^4} \cdot 1.5mm = 2.23N/mm^2[/math]
erhalten wir eine maximale Spannung von [math]2.23N/mm^2[/math] und sind damit weit von der zulässigen Spannung [math]\sigma _{zul} = 1000 N/mm^2[/math] entfernt.
Verformung und Belastung des Oberschenkels
Auf den Oberschenkel wirkt, wie schon erwähnt, eine Torsion durch die Kraft F und über den Hebel des Unterschenkels.
Aber es wirkt nicht nur die Torsion, sondern auch die Kraft F direkt, denn:
Wie man sieht geht die Kraft F nicht verloren, sondern wirkt auch neben der Torsion noch als Moment wie am Unterschenkel.
Durchbiegung / Moment
Daher müssen wir zunächst mal die Durchbiegung des Oberschenkels berechnen:
Da der Querschnitt der gleiche ist, ist [math]I_{yy} = 67.5mm^4[/math]
Die Durchbiegung berechnet man auch auf die gleiche Art:
[math]w_{2max} = \frac{F \cdot l^3}{3 \cdot E \cdot I} = \frac{F \cdot 80^3}{3 \cdot E \cdot I_{yy}} = 0.057mm[/math]
Der Oberschenkel biegt sich also durch das Moment um 0.057mm durch.
Jetzt berechnen wir die Spannung im Oberschenkel aufgrund des Momentes der Kraft F, ohne Torsion:
Genau wie beim Unterschenkel:
[math]M_{y2(max)} = M_{y(x2=80mm)} \Rightarrow M_{y2(max)} = 1N * 80mm = 80N/mm[/math]
Setzen wir das maximale Moment nun in die Spannungsgleichung ein
[math]\sigma_{xx max}(x, z) = \frac{M_{y2(max)}}{I_{yy}} \cdot z_{max} = \frac{80N/mm}{67.5mm^4} \cdot 1.5mm = 1.78N/mm^2[/math]
erhalten wir eine maximale Spannung von [math]1.78N/mm^2[/math] und sind damit natürlich ebenfalls weit von der zulässigen Spannung [math]\sigma _{zul} = 1000 N/mm^2[/math] entfernt.
Torsion
Jetzt kommt der interessante Teil des Oberschenkels, die Torsion.
Torsion zu berechnen ist wesentlich schwerer als die Durchbiegung mit reiner Druck-/Zugspannung.
Denn hier treten, wie erwähnt, Schubspannungen auf und der Körper verformt sich und verbiegt sich nicht nur. Will man das ganz genau berechnen ist es ein erheblicher Rechenaufwand mit einigen Umformungen von Gleichungen, Integralen etc...
Deswegen beschränke ich mich hier auf in Tabellen aufgeführte Näherungswerte für bestimmte Querschnitte, die bei weitem genau genug sind!!!
Die Materialkennwerte für Torsion:
Das Schubmodul G ist hier equivalent zum E - Modul und gibt einen Wert für das "Widerstreben"/die Steifigkeit gegenüber Verdrehung.
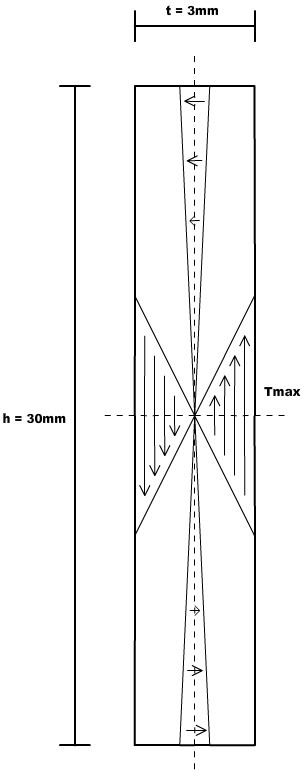
Der Oberschenkel-Querschnitt sieht folgendermaßen aus:
Üben wir nun eine Torsion auf den Oberschenkel aus, passiert folgendes:
Die Spannungen laufen um den Querschnitt herum und wirken jeweils in entgegengesetzte Richtungen zueinander. Dabei treten die maximalen Spannungen jeweils in den Mitten der Seiten auf.
Das ist die erwähnte Scherung, für die alle Materialien anfällig sind. Besonders trifft dies auf Materialien mit Fasern zu, also Holz und auch GFK oder CFK.
Um nun die Torsion zu berechnen benötigen wir wieder einige Werte die Bezug auf das Material und den Querschnitt nehmen:
Wir benötigen also nun folgende Werte:
[math]I_T:[/math] Flächenträgheitsmoment bei Torsion
[math]W_T:[/math] Torsionswiderstandsmoment
[math]M_T:[/math] Torsionsmoment
um diese gesuchten Werte zu berechnen:
[math]\tau_{max}:[/math] max. Spannung durch Torsion
[math]\zeta:[/math] Verdrillung
[math]\phi:[/math] Verdrehwinkel
Ohne Tabellenwerk für bestimmte Querschnitte wären die Rechnungen für Flächenträgheitsmoment bei Torsion und Torsionswiderstandsmoment jetzt sehr aufwändig, allerdings auch etwas genauer, da das Tabellenwerk natürlich etwas allgemein ist, reicht hier aber völlig aus.
Also das Tabellenwerk sagt:
Wenn [math]t\lt\lth[/math] , also wenn die Dicke des Materials wesentlich kleiner als die Breite ist, und das ist hier ja der Fall,
dann
[math]I_T = \frac{1}{3} \cdot h \cdot t^2 = 270mm^4[/math]
[math]W_T = \frac{1}{3} \cdot h \cdot t^3 = 90mm^4[/math]
Gut, jetzt brauchen wir das Torsionsmoment [math]M_T:[/math]
[math]M_T = F \cdot r = 1N * 100mm = 100N/mm[/math] , Moment ist Kraft * Hebelarm und hier ist ja der Unterschenkel (100mm) der Hebelarm.
Jetzt können wir die max. Spannung berechnen:
[math]\tau_{max} = \frac{M_T}{W_T} = 1.11N[/math]
Ein Vergleich mit der zulässigen Schubspannung zeigt, dass die Differenz nicht mehr ganz so hoch ist, aber wir sind immer noch weit entfernt:
[math]\tau_{zul} = 70 N/mm^2[/math]
[math]\tau_{max} 1.11 N/mm^2[/math]
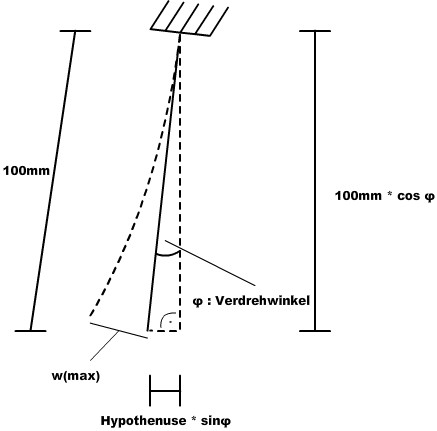
Um die komplette Durchbiegung am freien Ende zu bestimmen fehlt noch eine Größe. Wir wissen nun zwar wie weit sich Ober- und Unterschenkel aufgrund des Momentes durchbiegen.
Aber der Oberschenkel verdreht sich ja auch, was sich natürlich auch auf die maximale Durchbiegung am freien Ende auswirkt:
[math]\zeta = \frac{M_T}{G \cdot I_T} = \frac{100N/mm}{5600N/mm^2 \cdot 270mm^4} = 6.614 \cdot 10^{-5}[/math]
[math]\varphi = \zeta \cdot L = 5.291 \cdot 10^{-3}[/math] ,L: Länge das Oberschenkels, also 80mm
Der Oberschenkel verdreht sich also um 0.00529°
Jetzt sind wir fast fertig, wir müssen nur noch die Durchbiegung von Unterschenkel, Oberschenkel und Verdrehung durch Torsion zusammenrechnen:
[math]w_{ges} = w_{max} + w_{2max} + (Hypothenuse \cdot \sin\varphi) = 0.11mm + 0.057mm + 0.00923mm = 0.17623mm \approx 0.18mm[/math]
Die gesamte maximale Durchbiegung am freien Ende beträgt also 0.18mm.
Schlusswort
Die Verformung sowie die auftretenden Spannungen sind in diesem Fall ziemlich klein. Das liegt zum einem an dem geringen Gewicht und der geringen Größe des Hexapod sowie der sehr hohen Stabilität und Steifigkeit von GFK.
Mit Lexan (Plexyglas) und/oder einem schwereren Hexapoden könnte man bei zu geringem Querschnitt schon an die Grenzen stoßen.
Wozu ist das Ganze gut?
Hiermit könnt ihr zum einen berechnen wie stark ihr bestimmte Teile eurer Roboter auslegen müsst. Warum wesentlich mehr Material/Querschnitt nutzen als es nötig ist?
Gewichtsersparniss ist, so denke ich, immer von großem Vorteil, vor allem bei akkubetriebenen Robotern.
Zum anderen könnt ihr euch eventuell den einen oder anderen Prototypen sparen, eine umfangreiche Planung kann nie verkehrt sein.