Inhaltsverzeichnis
Wozu benutzt man Filter?
Für Filter gibt es eine ganze Menge Anwendungen.
Als erstes Beispiel nehmen wir uns mal einen Verstärker her, einen einfachen. Einen Transistor in Emitterschaltung zum Beispiel. Am Eingang dieser Schaltung liegt die Basis des Transistors, beschaltet mit einem Vorwiderstand von Vcc aus. Dieser dient dazu, den Arbeitspunkt des Transistors festzulegen und "zieht" die Basis des Transistors zum Beispiel auf 0,70 Volt.
Was passiert wenn man nun ein Signal anlegt, beispielsweise ein Audiosignal, welches zwischen 0,1 Volt und -0,1 Volt schwingt? Die Basis wird auf eben diese (im Mittel) 0 Volt heruntergezogen, und der Strom, der eigentlich für die Basis vorgesehen war, fließt nun einfach in die Signalquelle ab.
Hier schafft ein Entkopplungskondensator, den man zwischen Signalquelle und Basis des Transistors schaltet, Abhilfe: Die Spannung zwischen dessen Anschlüssen steigt durch den abfließenden Strom langsam an. Die Spannung an der zum Transistor gewandten Seite steigt also an, und irgendwann ist die Spannung soweit gestiegen, dass durch die Basis des Transistors wieder der entsprechende Strom fließen kann. Durch den Kondensator fließt dann kein Gleichstrom mehr.
Die Wechselspannung, in diesem Fall das Audiosignal, wird dagegen durchgelassen. Dabei fließt nämlich während der positiven Halbwelle Strom in die Schaltung herein, bei der negativen Halbwelle des Signals dagegen fließt der Strom wieder heraus. Diese Strompulse sind so kurz, dass der Kondensator seine Spannung dabei kaum ändert, sie werden also fast ungehindert durchgelassen.
Als zweites Beispiel nehmen wir uns nochmal Audio-Kram her: Wir haben nen Tieftöner, den wir an unsere Stereoanlage anschließen wollen. Die tiefen Frequenzen soll er ruhig wiedergeben - die hohen Frequenzen jedoch nicht, denn für die sind die Hochtöner zuständig.
Eine Spule, die hier in Reihe zum Lautsprecher geschaltet wird, erfüllt diese Bedingungen. Wenn ein Signal an die Kombination aus Lautsprecher und Spule angelegt wird, steigt der Strom, bedingt durch die Induktivität der Spule, nur langsam an. Bei tiefen Frequenzen fällt das kaum auf, denn eine Halbwelle ist lang genug, um den Strom durch den Lautsprecher und die Spule zu erhöhen. Bei hohen Frequenzen dagegen sind die Halbwellen so kurz, dass sich kein nennenswerter Stromfluss einstellen kann - die Signale werden von der Spule blockiert.
Zur Glättung von Spannungen und / oder Strömen werden auch Filter eingesetzt. Eine Kombination aus Spule und Kondensator (LC-Filter) setzt man beispielsweise häufig vor der ADC-Versorgung von Mikrocontrollern ein. Diese Filter filtern doppelt: Wenn die Versorgungsspannung plötzlich leicht abfällt, ändert sich zunächst der Strom in der Spule, aber wie gesagt wurde, durch die Induktivität verlangsamt. Wenn der Strom etwas abgefallen ist, wird das zweite Filterelement - der Kondensator - aktiv, denn durch ihn muss zuerst ein Strom fließen, damit sich die Spannung am Ausgang der Schaltung ändern kann.
- Phantomspeisung (gecancelt: Gebräuchliche Systeme wie PoE brauchen dafür afaik keine echten Filter.)
Arten von Filtern
Nun gibt es aber zig verschiedene Möglichkeiten, Filter aufzubauen, noch dazu ist jede nur für spezielle Anwendungen geeignet.
Man unterteilt Filter zunächst in aktive Filter und passive Filter: Passive Filter sind solche, die nur aus passiven Bauteilen bestehen. Dazu gehören die oben angesprochenen Kondensatoren, Spulen und Widerstände, aber auch Quarze.
Aktive Filter enthalten als aktive Komponente meist einen Operationsverstärker. Der Vorteil liegt auf der Hand: Der Ausgang des OpAmps ist auch der Ausgang des Filters, der damit auch ruhig bis einige Milliampere belastet werden kann - bei passiven Filtern ist dies meistens nicht ohne weiteres möglich, die Ausgangsspannung würde sich dabei ändern. Der Nachteil sollte auch klar sein: Ein OpAmp, und jede andere aktive Komponente auch, braucht eine Versorgungsspannung. Für eine Frequenzweiche in einer passiven Standbox (d.h. der Verstärker ist nicht integriert) sind aktive Filter dadurch ungeeignet.
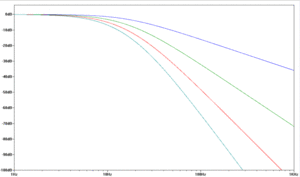
Weiterhin unterscheidet man Filter nach verschiedenen Ordnungen. Die Ordnung spiegelt dabei die Anzahl der frequenzabhängigen Bauteile wieder. Ein Filter höherer Ordnung, beispielsweise die oben beschriebene Kombination aus Spule und Kondensator, hat eine bessere Trennschärfe. Das bedeutet, dass der Abstand zwischen Frequenzen, die durchgelassen werden, und Frequenzen, die gesperrt werden, kleiner ist.
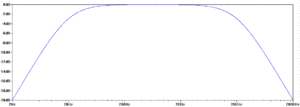
Nun gut, im Bild rechts sieht man schon dass das so nicht ganz stimmt: Jede Frequenz wird noch irgendwie durchgelassen, aber die Dämpfung, die in dB gemessen wird, wird immer stärker. Man müsste also eigentlich sagen, dass der Abstand der Frequenzen, die als durchgelassen bezeichnet werden können und der Frequenzen, die als gesperrt bezeichnet werden können, kleiner ist. Ab welcher Dämpfung eine Frequenz als gesperrt oder durchgelassen bezeichnet werden kann, das hängt wiederum von der Anwendung ab. In Audioanwendungen reicht ein Filter 1. Ordnung meist völlig aus, aber um beispielsweise ein PWM-Signal in eine Gleichspannung zu wandelt, muss eine bestimmte Frequenz unbedingt möglichst schwach gedämpft durchgelassen werden, während die PWM-Frequenz möglichst stark gedämpft werden soll. Deshalb nutzt man hierfür vorwiegend Filter höherer Ordnungen.
Zuletzt unterteilt man Filter noch in verschiedene Charakteristiken, namentlich Tiefpässe, Hochpässe, Bandpässe und Bandsperren.
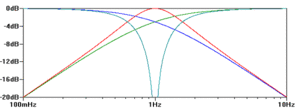
- Tiefpässe lassen tiefe Frequenzen durch und sperren hohe Frequenzen. (siehe blaue Kurve im Bild.) Eine typische Anwendung wäre die Glättung eines Signals mithilfe einer Kombination aus Spule und Kondensator.
- Hochpässe machen das Gegenteil: Sie sperren tiefe Frequenzen und lassen hohe Frequenzen durch. (siehe grüne Kurve im Bild.) Beispiele wären eine Gleichspannungsentkopplung oder eine Frequenzweiche für einen Hochtonlautsprecher.
- Bandpässe sperren hohe und tiefe Frequenzen - Ein bestimmter Frequenzbereich wird jedoch durchgelassen. (siehe rote Kurve im Bild.) Eine Anwendung hierfür wäre eine Frequenzweiche vor einem Mitteltöner (Sorry für die ganzen Beispiele aus dem Audiobereich, fällt vielleicht wem was besseres ein? Passiv-PFC würde mir einfallen, würde aber ne längere Erläuterung notwendig machen.)
- Bandsperren sind das Gegenstück zu den Bandpässen: Hohe und tiefe Frequenzen werden durchgelassen, ein bestimmter Frequenzbereich wird gesperrt. (siehe türkise Kurve im Bild.) Eine solche Schaltung kann beispielsweise verwendet werden, um die möglicherweise bei Datenübertragungen über Modem störenden Gebührenimpulse aus der Telefonleitung herauszufiltern.
Wie man sieht, sind die Bezeichnungen so gut wie selbsterklärend.
Realisierung
Wenn man einen Filter für eine bestimmte Anwendung berechnen will, braucht man folgende Informationen:
- Die Grenzfrequenz. Das ist die Frequenz, ab der die Ausgangsspannung gegenüber der Eingangsspannung um 3dB abgeschwächt wird - das entspricht in etwa einer Abschwächum um den Faktor 1,414, genauer um [math]\sqrt{2}[/math]
- Die Ordnung des Filters. Diese ergibt sich aus den Anforderungen in der Anwendung.
- Ob der Filter aktiv oder passiv ausgeführt werden soll
Alle Arten von Filtern, also solche 1. Ordnung, 2. Ordnung, Tiefpässe, Hochpässe etc. lassen sich sowohl Passiv als auch Aktiv aufbauen. Filter höherer als 2. Ordnung lassen sich immer als Verknüpfung von Filtern 1. und 2. Ordnung realisieren (bei passiven Filtern in der Regel mit einem Verstärker dazwischen). Beginnen wir zunächst mit den passiven Filtern:
Passiv
1. Ordnung, Tiefpass und Hochpass
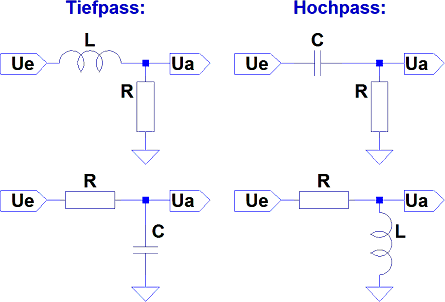
Für Tief- und Hochpässe 1. Ordnung gibt es zwei Möglichkeiten: Entweder man schaltet das frequenzabhängige Bauteil vor einen Lastwiderstand (beispielsweise einen Lautsprecher), oder man schaltet den Widerstand vor das frequenzabhängige Bauteil. Wie das dann aussieht, zeigt die folgende Abbildung:
Ue ist die Eingangsspannung, vor dem Filter, und Ua ist die Spannung, die am Ausgang der Schaltung anliegt um weiterverarbeitet zu werden. Die obigen Aufbauten, mit dem frequenzabhängigen Bauteil vor dem Lastwiderstand, bieten sich an, wenn man bereits einen Lastwiderstand - beispielsweise einen Lautsprecher - gegeben hat. Den Widerstand R ersetzt man dann durch diese Last - und hat ein Bauteil weniger zu verbasteln.
Das RC-Glied (links unten) bietet sich an, wenn man einen Tiefpassfilter mit hoher Eingangsimpedanz benötigt. Das ist beispielsweise der Fall, wenn man eine Referenzspannung glätten möchte.
Das RL-Glied bietet sich meines Wissens überhaupt nicht an :D, da für die im Hobbybereich gängigen Frequenzen entweder ein sehr kleiner Widerstand R oder eine sehr große Spule nötig würde. Lösung 1 hat dann einen extrem kleinen Eingangswiderstand, Lösung 2 verbraucht massig Platz und ist teuer.
Die Berechnungen sind, egal ob Hochpass oder Tiefpass, jeweils identisch. Bei einer Spule als frequenzabhängiges Bauteil gilt:
[math]L = \frac{R}{2\pi*f_g}[/math]
Wird dagegen ein Kondensator benutzt, gilt:
[math]C = \frac{1}{2\pi*f_g*R}[/math]
Passiv, 2. Ordnung
Bei Filtern zweiter Ordnung gibt es neben der charakteristischen Frequenz noch einen 2. Parameter, die Güte. Diese beschreibt die Schwingfähigkeit des Filters, also etwa wie lange der Filter nach einem kurzen Impuls nachschwingt. Filter hoher Güte (nicht als Qualitätsmassstab) geben einen schärferen Übergang von Durchlass zum Sperren. Als Nachteil braucht es aber etwas Zeit bis der Filter eingeschwungen ist. Ob eine hohe oder niedriger Güte gewünscht ist, hängt von der Anwendung ab: Im Audiobereich nutzt man Filter mit eher geringer Güte und dadurch schwacher Schwingneigung. Wenn aber eine hohe Trennschärfe (etwa Radioempfang) gefordert ist, kann man diese durch Erhöhung der Güte verbessern. Bei Filtern mit hoher Güte sinkt die Dämpfung beim Übergang zum Sperrbereich des Filters erst ab, in einem bestimmten Bereich wird sie sogar kleiner als 1. Das heißt das Signal wird sogar noch verstärkt. Danach steigt die Dämpfung relativ schnell an. Bei einer Güte, die kleiner ist als die Wurzel aus 1/2 (ca. 0,707) tritt dieses sogenannte Überschwingen des Frequenzgangs nicht auf. Diese Güte ist auch die gebräuchlichste, sie ist meistens ein guter Kompromiss. Filter mit dieser Güte haben eine Butterworth-Charakteristik. Daneben gibt es noch andere: Ein Filter mit Tschebyshev-Charakteristik ist jeder Filter mit einer Güte, die größer ist als die Wurzel aus 1/2. Bei diesen Filtern tritt besagtes Überschwingen auf, je höher die Güte, desto stärker ist das Überschwingen. Ein Filter mit Bessel-Charakteristik hat eine Güte von Wurzel aus 1/3. Die Trennschärfe bei diesen Filtern ist schlechter als bei Filtern mit Butterworth-Charakteristik, aber Signale, deren Frequenzanteile im Durchlassbereich liegen, werden nicht so stark verzerrt.
Bandpass
Bei diesen Arten von Filtern ist die Berechnung einen Tacken komplizierter. Bandpass und Bandsperre sind mindestens Filter 2. Ordnung. Im Grunde haben diese Filter eine obere und eine untere Grenzfrequenz, so dass verschieden große Frequenzbereiche beeinflusst werden können.
Am einfachsten ist es dann, zwei einzelne Filter zu dimensionieren, nämlich einen Hochpass und einen Tiefpass und diese dann zu einem Filter zusammenzufassen. Aufgrund von Resonanz ü.ä. entspricht der entstehende Frequenzgang nicht dem, der entstehen würde, wenn man einfach die Dämpfungen der beiden Filter zusammenrechnet. Solange der Filter ein ganzes Frequenzband durchlassen soll, macht dies aber in den seltensten Fällen einen Unterschied. Wenn aber nur eine Frequenz durchgelassen werden soll, unterscheidet sich der Frequenzgang stark von dem der Einzelnen Filter. Es gibt dann eine Resonanzfrequenz, bei der die Dämpfung extrem gering wird. Wenn man sich von der Resonanzfrequenz wegbewegt, steigt die Dämpfung erst sehr schnell an, und geht schließlich in einen Abfall um 20dB / Dekade (Spannung proportional oder antiproportional zur Frequenz) über.
Ein Problem gibt es aber dabei: Wenn die Abweichungen der Bauteile zu groß sind (und Kondensatoren sowie Spulen haben nunmal meistens große Toleranzen), wird die Frequenz möglicherweise nicht getroffen, und der Filter macht nicht das was er soll. Abhilfe schafft entweder die Verwendung von Bauteilen mit geringen Toleranzen (teuer!) oder eine Abgleich durch eine variable Kapazität oder Induktivität. Alternativ kann teilweise ein Filter höherer Ordnung mit einem etwas größerem des Frequenzband genutzt werden. Das gleiche gilt übrigens bei Bandsperren!
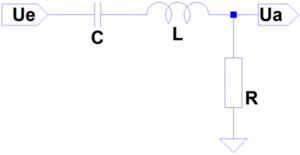
Ein Beispiel zur Berechnung: Nehmen wir an, wir brauchen einen Bandpass, der das hörbare Frequenzband von 20 Hertz bis 20 Kilohertz durchlässt. Diese Frequenzen sollten dann zugleich die Grenzfrequenzen des Filters sein. Wir berechnen dann einen Hochpassfilter, um Frequenzen unter 20 Hertz zu sperren, und einen Tiefpass, der Frequenzen über 20 Kilohertz sperren würde. Da ein Lastwiderstand, ein Breitbandlautsprecher mit einer Impedanz von 8 Ohm, gegeben ist, benutzen wir die oberen Aufbauten aus der obigen Grafik. Wir erhalten für die Induktivität [math]L \approx 63\mu H[/math] und für den Kondensator [math]C \approx 1000\mu F[/math].
Die Schaltung wird in dem Bild oben rechts gezeigt, die beiden Filter werden sozusagen hintereinandergeschaltet.
Das Ergebnis ist in dem Bild darunter dargestellt: Die Grenzfrequenzen liegen mit ausreichender Genauigkeit bei den erwarteten Frequenzen von 20 Hertz und 20 Kilohertz.
Bandsperre
Bei einer Bandsperre verfährt man fast genauso. Man berechnet einen Tiefpassfilter für die untere Grenzfrequenz und einen Hochpassfilter für die obere Grenzfrequenz. Die Frequenzanteile, die dann zwischen den Grenzfrequenzen liegen, werden mehr oder weniger stark gesperrt, je nachdem, wie weit sie von den Grenzfrequenzen entfernt sind. In der geometrischen Mitte der beiden Frequenzen tritt eine Resonanz auf, die Sperrwirkung des Filters ist dann fast unendlich groß, sofern man ideale Bauteile hat.
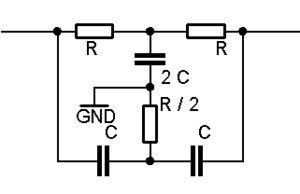
Bei einer Bandsperre werden die beiden frequenzabhängigen Bauteile parallel geschaltet. Die Schaltung sieht dann so aus wie in der nebenstehenden Abbildung.
Für die Bandsperre gibt es noch eine zweite Möglichkeit, ohne Induktivität. Damit ist diese Schaltung gut als Filter für niedrige Frequenzen wie z.B. 50 Hz oder 100 Hz geeignet. Die erreichbare Sperrwirkung des Filters hängt davon ab, wie gut das Verhältnis der Werte stimmt. Die Güte liegt bei dieser Schaltung fest bei 1/2 - mit aktiven Variationen der Schaltung sind höhere Güten möglich.
Aktiv
Bei relativ niedriger Frequenz, wie im Audiobereich sind Induktivitäten ziemlich unhandliche Bauteile und alles andere als ideal. Mit Hilfe von Verstärkern lassen sich auch Filter mit höherer Güte (Q > 0.7) ohne Induktivitäten, nur mit Widerständen, Kondensatoren und halt dem Verstärker (heute in der Regel ein Operationsverstärker) aufbauen.
Die Filter 1. Ordnung sind oft auch weiter passive Filter mit einem nachgeschalteten Verstärker. Eine Ausnahme sind hier die Extremfälle Integrator und Differentiator, und ein Allpassfilter (Phasenschieber).
Die typischen aktiven Filterschaltungen nutzen einen Operationsverstärker für einen Filter 2. Ordnung. Dabei gibt es mehrere Möglichkeiten der Realisierung. Zur Berechnung der passenden Widerstandswerte und Kapazitäten gibt es spezielle Programme zum Filter-Design (siehe Weblinks). Damit kann dann auch gleich der Frequenzgang im voraus berechnet werden.
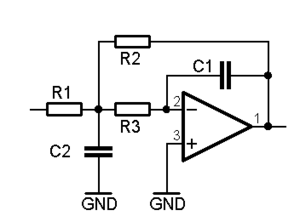
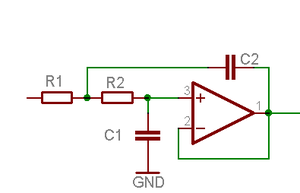
Multiple-Feedback Filter
Diese Schaltungsform ist vor allem angebracht für Filter mit hohem Q. Im Durchlassbereich wird das Signal invertiert. Der Hochpassfilter entsteht aus dem Tiefpass indem man die Widerstände und Kondensatoren vertauscht. Allerdings ist der Hochpass von der Stabilität problematisch.
.
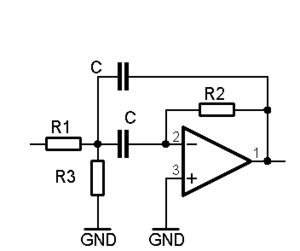
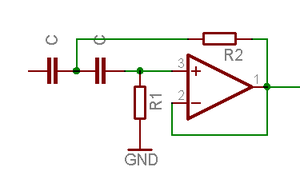
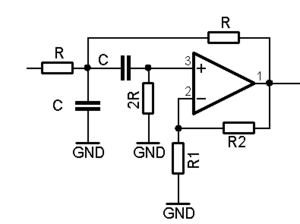
Sallen-Key Filter
Diese Schaltung ist vor allem angebracht für Filter mit niedrigem Q ( < 2). Im Durchlassbereich wird das Signal nicht invertiert und in der Regel auch nicht verstärkt. Bei der Wahl der Kapazitäten und Widerstände gibt es mehrere Möglichkeiten. Der einfache Fall mit 2 gleichen Widerständen und 2 gleiche Kondensatoren gibt für den Hochpass und Tiefpass eine Grenzfrequenz von 0,16 / (RC) und eine Güte von 0,5.
.
weitere Filterschaltungen
Auch bei normalen Verstärkerschaltungen wird oft die Bandbreite nach oben und unten auf den nötigen Bereich begrenzt. Die Filterfunktion ist dabei eher Nebensache und eine Kombination aus einem Hochpass und Tiefpass jeweils 1. Ordnung genügt.
Filter mit geschalteten Kondensatoren (switched capacitor filter)
Um die Frequenz eines aktiven Filters höherer Ordnung zu verstellen muss man oft mehrere Widerstände synchron verstellen. Neben der relativ neuen Möglichkeit über elektronische Potis gibt es die alternative Widerstände durch kleine Ladungspumpen zu ersetzen. Statt eines kontinuierlichen Stromes wird die Ladung in einem Kondensator und elektronischen Schaltern in kleinen Portionen transportiert. Für niedrige Frequenzen verhält sich das dann wie ein Widerstand, umgekehrt proportional zur relativ hohe Umschaltfrequenz. Man kann so über die Umschaltfrequenz (z.B. 1 MHz) die Grenzfrequenz (z.B. 1 kHz) eines aktiven Filters, auch höherer Ordnung verstellen. Für diese Anwendung gibt es spezielle ICs.
Weblinks