An diesem Artikel arbeitet gerade Mitglied BMS.

Am besten momentan noch keine gravierenden Ergänzungen / Änderungen vornehmen.

Dieser Hinweis verschwindet wenn der Autor soweit ist. Sollte dieser Hinweis länger als drei Tage auf einer Seite sein, bitte beim Autor BMS per PM / Mail oder Forum nachfragen ob er vergessen wurde.

Dieser Artikel behandelt die Grundlagen zu Kühlkörpern.

Fehler beim Erstellen des Vorschaubildes: Datei fehlt

Verschiedene Kühlkörper, links ein TO220-Gehäuse zum Größenvergleich

Einleitung

Wieso sind überhaupt Kühlkörper in technischen Geräten erforderlich?

Kein Gerät kann einen 100-prozentigen Wirkungsgrad erzielen und somit tritt Verlustleistung auf. Diese Verlustleistung führt zur Erwärmung der Bauteile. Kühlkörper sollen die Entwärmung verbessern, indem die entstehende Wärme auf eine große Fläche verteilt wird und durch Konvektion an der Luft auskühlen kann. Die Temperatur an den heißen Bauteilen ist mit Kühlkörper geringer als ohne Kühlkörper.

Wieso sind hohe Bauteiltemperaturen ungünstig?

Die Lebensdauer aller elektronischen Bauteile ist stark von der Temperatur abhängig. Als Faustregel gilt: Eine Temperaturerhöhung um 10 Grad führt zur Halbierung der Lebensdauer. Außerdem gibt es Grenztemperaturen, die nicht überschritten werden dürfen. Beispielsweise dürfen Halbleiter keine Temperatur über 150°C erreichen. Platinenmaterial FR4 sollte 125°C (sog. Erweichungspunkt) nicht überschreiten. Extrembeispiele sind die Schmelztemperatur von Isolierungen, Lötzinn etc... sowie Brandgefahr durch hohe Temperaturen. Viele Bauteile können ohne vernünftige Kühlung nicht ihren vollen Funktionsumfang erreichen, liefern dann z.B. geringere Maximalströme oder es greift die Temperaturabschaltung. Anders formuliert: Die maximale Leistung eines Bauteils oder Geräts wird durch seine Entwärmung bestimmt! Zur eigenen Sicherheit bietet es sich zudem an, die Temperaturen niedrig zu halten, sodass man sich am Gerät nicht die Finger verbrennen kann ;)

Wärmeübertragung

Prinzipiell kann Wärmeübertragung über Wärmeleitung, Konvektion und Wärmestrahlung geschehen. In vielen Anwendungen treten mehrere Mechanismen gleichzeitig auf. Welcher Mechanismus hauptsächlich auftritt, ist von der mechanischen Anordnung, den Materialien und der Temperatur abhängig. Wärmeleitung und Konvektion sind die wichtigsten Arten der Wärmeübertragung, die in der Praxis auftreten. Nun zu den einzelnen Effekten:

Wärmeleitung
Bei der Wärmeleitung wird die Wärme über einen direkten mechanischen Kontakt (Bsp. IC [math]\rightarrow[/math]Kühlkörper) übertragen. Den beteiligten Materialien wird jeweils eine spezifische Wärmeleitfähigkeit [math]\lambda[/math] zugeordnet, dazu später mehr.

Konvektion
Mit Konvektion wird die Strömungsbewegung in Flüssigkeiten und Gasen bezeichnet. Praxisbeispiele sind die Wärmeabgabe eines Kühlkörpers an die Umgebungsluft oder auch eine Wasserkühlung. Von erzwungener Konvektion spricht man, wenn die Strömung durch z.B. einen Ventilator/Lüfter oder eine Wasserpumpe hervorgerufen wird. Im Vakuum kann keine Konvektion auftreten.

Wärmestrahlung
Wärmestrahlung ist elektromagnetische Strahlung (hauptsächlich Infrarot und sichtbares Licht), die vom heißen Festkörper abgestrahlt wird. Sie wird erst bei höheren Temperaturen relevant und ist bei den üblichen Kühlkörpertemperaturen meist zu vernachlässigen. Erwähnt werden soll zudem, dass Wärmestrahlung der einzige Mechanismus der Wärmeleitung ist, welcher im Vakuum auftreten kann. (Für Details zu Wärmestrahlung siehe auch: Plancksches Strahlungsgesetz und Schwarzer Strahler).

Materialien

Jedes Material besitzt eine spezifische Wärmeleitfähigkeit, welche angibt, wie gut dieses Material Wärme weiter transportieren kann. Die spezifische Wärmeleitfähigkeit ist unabhängig von der Geometrie des Materials, wird mit der Größe [math]\lambda[/math] (Lambda) ausgedrückt und erhält die Einheit [math]\frac{W}{m \cdot K}[/math].

Material	[math]\lambda[/math] in [math]\left[ \frac{W}{m \cdot K} \right][/math]
Silber	430
Kupfer	400
Aluminium	230
Silizium	140
Wärmeleitpaste	5 ... 10
Glas	0,7
Wasser	0,5
Platinenmaterial FR4	0,2 ... 0,5
Luft	0,02

Die meisten Kühlkörper werden aus Aluminiumlegierungen hergestellt. Für Aluminium spricht seine relativ hohe Wärmeleitfähigkeit, die hohe Verfügbarkeit und geringe Dichte. Im Vergleich zu Kupfer und Silber ist Aluminium deutlich kostengünstiger. Darüber hinaus lässt sich Aluminium mechanisch gut verarbeiten. Kupfer wird mit seiner höheren Wärmeleitfähigkeit z.B. bei Heatpipes eingesetzt.

todo

Wärmewiderstand [math]R_{th}=\frac{d}{\lambda \cdot A}[/math]

d: Materialdicke, welche für die Wärmeleitung relevant ist

[math]\lambda[/math]spezifische Wärmeleitfähigkeit des Materials

A: Querschnitts-/Kontaktfläche

Definitionen

Um vorauszusagen, wie sich die Temperaturen in einer Schaltung verhalten, bedient sich der Ingenieur - wie auch bei vielen anderen Anwendungen - eines Ersatzschaltbildes (ESB). Zur Erstellung eines thermischen Ersatzschaltbildes muss man sich aber zunächst mit den thermischen Größen vertraut machen.

Die Temperaturen werden mit dem griechischen Buchstaben Theta [math]\theta[/math] gekennzeichnet. Temperaturen werden in Grad Celsius (°C), Temperaturdifferenzen in Kelvin (K) angegeben. (Am Rande: Es existiert auch eine Kelvinskala mit dem absoluten Nullpunkt 0 K=-273,15°C). Die Temperaturen werden außerdem noch mit einem Index gekennzeichnet, abhängig von der mechanischen Stelle, an der sie auftreten:

Symbol	Index	Bedeutung
[math]\vartheta_{J}[/math]	J=Junction	Sperrschichttemperatur des Halbleiters
[math]\vartheta_{C}[/math]	C=Case	Gehäusetemperatur des Bauteils
[math]\vartheta_{H}[/math]	H=Heat Sink	Temperatur des Kühlkörpers
[math]\vartheta_{A}[/math]	A=Ambient	Umgebungstemperatur

Die Verlustleistung eines Bauteils beschreibt die Größe [math]P_{V}[/math] und wird, wie allgemein bekannt, in Watt angegeben.

Als neue Größe wird nun der thermische Widerstand eingeführt, dieser wird mit [math]R_{th}[/math] beschrieben und bekommt die Einheit [math]\frac{K}{W}[/math].

Für die thermischen Größen gibt es, ähnlich dem Ohmschen Gesetz, einen linearen Zusammenhang. Dieser lautet

[math]R_{th}=\frac{\vartheta_{ü}}{P_{V}}[/math]

todo

Vergleich elektrischer und thermischer Größen

Insgesamt können wir nun eine Analogie zwischen bekannten elektrischen Größen und den thermischen Größen angeben. Die schon gelernten Prinzipien zur Lösung linearer Netzwerke lässt sich auch bei den thermischen Ersatzschaltbildern anwenden.

elektrisch	thermisch
Spannung U	Temperatur [math]\vartheta[/math]
Strom I	Verlustleistung [math]P_{V}[/math]
Widerstand R	thermischer Widerstand [math]R_{th}[/math]

Statisches Ersatzschaltbild

Mit den thermischen Zusammenhängen haben wir uns inzwischen vertraut gemacht. Nun können wir damit beginnen, thermische Ersatzschaltbilder von einfachen Anordnungen zu erstellen. Mit solchen Modellen können Temperaturen, wie z.B. die Chiptemperatur, vorab berechnet werden. Für die Berechnung müssen Wärmewiderstände, Umgebungstemperatur und Verlustleistung bekannt sein, da sie in die Berechnung einfließen.

Bei den thermischen Ersatzschaltbildern kann man ein statisches oder ein dynamisches Ersatzschaltbild erstellen. Bei den statischen Ersatzschaltbilder wird davon ausgegangen, dass alle Größen zeitlich konstant sind, bzw. sofort ihre Solltemperatur entsprechend dem Modell annehmen. In der Realität dauert es natürlich eine gewisse Zeit, bis sich alle beteiligten Materialien aufgeheizt haben. Die Temperaturen des statischen Modells werden dabei erst nach einer bestimmten Zeit erreicht.

Für die meisten Anwendungen genügt es jedoch, das statische thermische Ersatzschaltbild zu erstellen und den Kühlkörper dem entsprechend zu dimensionieren. Die Kühlung wird z.B. auf die maximale oder die mittlere auftretende Verlustleistung dimensioniert. Es wurde bereits erwähnt, dass sich die Bauteiltemperatur auf dessen Lebensdauer auswirkt. Dabei gilt: je niedriger die Bauteiltemperatur, desto länger die zu erwartende Lebensdauer. Je nach Anwendung und Rahmenbedingungen muss eventuell ein Kompromiss zwischen Kühlkörpergröße/kosten und Gerätelebensdauer gewählt werden. Beispielsweise kann der verfügbare Platz, ein Gesamtgewicht oder eine Kostenvorgabe begrenzender Faktor sein. Für einen dauerhaften sicheren Betrieb muss der Kühlkörper und weitere beteiligte Materialien für den worst case ausgelegt oder sogar überdimensioniert werden.

Bauteil ohne Kühlkörper

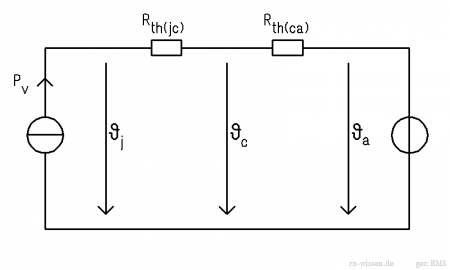
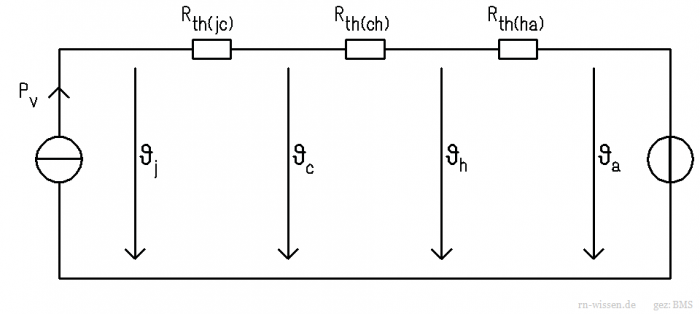
Um den Umgang mit den thermischen Ersatzschaltbildern zu lernen, soll zunächst mit einem einfachen Beispiel begonnen werden. In diesem Fall wird der Wärmeübergang von einem einzelnen Bauteil zu Luft betrachet, es kommt zunächst also noch kein Kühlkörper zum Einsatz. Das Ersatzschaltbild sieht in diesem Fall folgendermaßen aus:

Die am Bauteil entstehende Verlustleistung ist Ursache der Abwärme und wird im thermischen Ersatzschaltbild als ideale Stromquelle modelliert.

Die Abwärme gelangt nun über den Weg Sperrschicht (Junction) [math]\rightarrow[/math] Bauteilgehäuse (Case) [math]\rightarrow[/math] Umgebung (Ambient) nach außen. Im Ersatzschaltbild ist jeder Übergang als thermischer Widerstand modelliert. Die genauen Zahlenwerte der Wärmewiderstände lassen sich in der Regel dem Datenblatt des Bauteils entnehmen. Benötigt werden die Werte für [math]R_{th(jc)}[/math] und [math]R_{th(ca)}[/math]. In manchen Datenblättern findet man die Angabe [math]R_{th(ja)}[/math], was der Reihenschaltung aus den beiden vorher genannten Werten entspricht, also [math]R_{th(ja)}=R_{th(jc)}+R_{th(ca)}[/math].

Die Umgebungstemperatur wird als ideale Spannungsquelle modelliert. Sämtliche Spannungen im Ersatzschaltbild entsprechen den auftretenden Temperaturen.

Da es sich nun um ein lineares Netzwerk handelt, gelten hier ebenfalls die Kirchhoff'schen Gleichungen. Relativ leicht lässt sich nun die Temperatur am Bauteilgehäuse (Case) und der Sperrschicht (Junction) berechnen:

[math]\vartheta_{c}=\vartheta_{a}+R_{th(ca)} \cdot P_{V}[/math]

[math]\vartheta_{j}=\vartheta_{a}+R_{th(jc)} \cdot P_{V}+R_{th(ca)} \cdot P_{V}=\vartheta_{a}+(R_{th(jc)}+R_{th(ca)}) \cdot P_{V}=\vartheta_{a}+R_{th(ja)} \cdot P_{V}[/math]

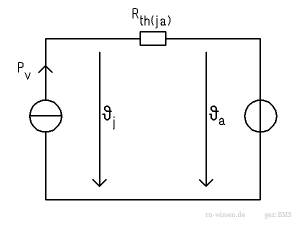
Da die thermischen Widerstände bei der Reihenschaltung auch zusammengefasst werden dürfen, beschreibt folgendes thermisches Ersatzschaltbild den gleichen Zusammenhang. Nachteil ist hier allerdings, dass die Temperatur am Gehäuse nicht modelliert wird.

Derating

Die Überlegungen zur Sperrschichttemperatur kann auch anders interpretiert werden. Gibt man die Sperrschichttemperatur vor, kann man die maximal erlaubte Verlustleistung des Bauteils in Abhängigkeit der Umgebungstemperatur bestimmen. Die folgende Formel erhält man aus Umformung der oberen Gleichung:

[math]P_{V} \leq \frac{\vartheta_{j}-\vartheta_{a}}{R_{th(ja)}}[/math]

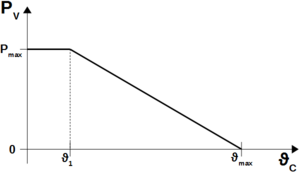
Bei Halbleitern darf idR. die Sperrschichttemperatur nicht 150°C überschreiten. Der thermische Widerstand wird hauptsächlich durch das Gehäuse vorgegeben. Aus der Formel sieht man nun folgendes: Je höher die Umgebungstemperatur, desto geringer fällt die maximal erlaubte Verlustleistung aus. Diesen Zusammenhang bezeichnet man auch als Derating. Der typische Verlauf sieht meist so aus:

Die Derating-Formel gilt im Bereich [math]\vartheta_{1} ... \vartheta_{max}[/math]. Für Temperaturen unter [math]\vartheta_{1}[/math] darf die Maximalleistung [math]P_{max}[/math]des Bauteilgehäuses nicht überschritten werden. [math]\vartheta_{1}[/math] liegt bei meist 25°C. Den genauen Verlauf kann man dem Datenblatt des betreffenden Bauteils entnehmen.

Beispielrechnung

Ein Spannungsregler vom Typ 7805 im TO220-Gehäuse soll ohne Kühlkörper betrieben werden. Wie hoch ist die maximal erlaubte Verlustleistung, wenn die Sperrschichttemperatur 120°C nicht überschreiten soll und die Umgebungstemperatur 25°C beträgt?

Zunächst werfen wir einen Blick ins Datenblatt des Spannungsreglers und entnehmen die Angaben für die thermischen Widerstände. Dann halten wir alle gegebenen Größen fest:

Gegeben
- [math]R_{th(jc)}=5 \frac{K}{W}[/math] (aus dem Datenblatt)
- [math]R_{th(ja)}=62 \frac{K}{W}[/math] (aus dem Datenblatt)
- [math]\vartheta_{j}=125°C[/math]
- [math]\vartheta_{a}=25°C[/math]
Gesucht
- [math]P_{v,max}[/math]
Rechnung
Wir verwenden die Formel von oben und erhalten als Ergebnis

[math]P_{V,max} = \frac{\vartheta_{j}-\vartheta_{a}}{R_{th(ja)}} = \frac{120°C-25°C}{62\frac{K}{W}} = \frac{95K}{62\frac{K}{W}} \approx 1,5 Watt[/math]

Die maximal erlaubte Verlustleistung des Spannungsreglers ohne Kühlkörper darf demnach 1,5 Watt nicht überschreiten.
Zusatz
Mit unserem Ersatzschaltbild können wir außerdem die Temperatur des Gehäuses (Case) des Spannungsreglers angeben. Dafür benötigen wir noch die Angabe [math]R_{th(ca)}[/math], welche allerdings im Datenblatt nicht angegeben ist.

Da wir aber wissen, dass [math]R_{th(ja)}=R_{th(jc)}+R_{th(ca)}[/math] gilt, können wir die fehlende Größe ausrechnen. Diese ist

[math]R_{th(ca)}=R_{th(ja)}-R_{th(jc)}=62\frac{K}{W}-5\frac{K}{W}=57\frac{K}{W}[/math].

Nun lässt sich die Gehäusetemperatur berechnen:

[math]\vartheta_{c}=\vartheta_{a}+R_{th(ca)} \cdot P_{V}=25°C+57\frac{K}{W} \cdot 1,5 W \approx 111 °C[/math]
Bemerkung
In der Praxis wird einem TO220-Gehäuse ungekühlt eine maximale Verlustleistung von 1 Watt zugerechnet. Die Temperaturen sind niedriger, die Lebensdauer des Bauteils höher.

Bauteil mit Kühlkörper und T.I.M.

Der Betrieb eines ICs ohne Kühlkörper, wie im vorigen Abschnitt beschrieben, funktioniert nur bei kleinen Leistungen und führt meist auch zu einer verringerten Lebensdauer des Bauteils. Viele Bauteile können ihre angegebenen Maximalwerte nur bei vernünftiger Kühlung erreichen. In diesem Abschnitt wird nun ein typisches Szenario mit Kühlkörperberechnung vorgestellt.

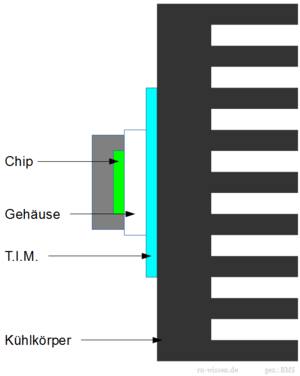
Befassen wir uns zunächst mit der typischen mechanischen Anordnung. Das zu kühlende IC wird thermisch an einen Kühlkörper gekoppelt. In der Praxis wird man das IC aber nicht direkt auf dem Kühlkörper befestigen, sondern über ein sogenanntes thermisches Interface-Material (T.I.M.), um Unebenheiten und mechanische Abstände auszugleichen oder um für Insolierung zu sorgen. Details zum T.I.M. folgen im Unterabschnitt. Die typische Anordnung zeigt die folgende Abbildung.

Folgende thermischen Widerstände treten hier in Kraft:

[math]R_{th(jc)}[/math] für den Übergang Chip zu Bauteilgehäuse
[math]R_{th(ch)}[/math] für den Übergang Bauteilgehäuse zu Kühlkörper (also über das T.I.M.)
[math]R_{th(ha)}[/math] für den Übergang Kühlkörper zur Umgebung

Aus diesen thermischen Widerständen wird ein thermisches Ersatzschaltbild angefertigt. Dieses zeigt die nächste Abbildung.

Zunächst soll die Formel zur Berechnung der Chiptemperatur aufgestellt werden, die Formel erhält man wieder durch die Anwendung der Kirchhoffschen Gleichungen im Ersatzschaltbild.

[math]\vartheta_{j}=\vartheta_{a}+(R_{th(jc)}+R_{th(ch)}+R_{th(ha)}) \cdot P_{V}[/math]

Die Formel wird in der Praxis jedoch in einer anderen Form benötigt. Meist steht man als Entwickler vor der Aufgabe, den erforderlichen thermischen Widerstand [math]R_{th(ha)}[/math] des Kühlkörpers zu bestimmen, sofern die Größen Umgebungstemperatur, Sperrschichttemperatur, Verlustleistung sowie die verbleibenden thermischen Widerstände gegeben sind. Anhand des berechneten Wärmewiderstands des Kühlkörpers können dann aus Produktkatalogen geeignete Kühlkörper bestimmt werden.

Wir müssen dafür also die Gleichung nach [math]R_{th(ha)}[/math] auflösen. Wir erhalten die praxisübliche Berechnungsformel:

[math]R_{th(ha)}=\frac{\vartheta_{j}-\vartheta_{a}}{P_{V}}-R_{th(jc)}-R_{th(ch)}[/math]

In manchen Quellen sind enthält diese Formel außerdem Korrekturfaktoren, die z.B. die Einbaulage o.ä. berücksichtigen können.

Beispielrechnung

Für einen Spannungsregler vom Typ 7805 im TO220-Gehäuse soll ein Kühlkörper dimensioniert werden. Die Eingangsspannung des Reglers beträgt 12V, die Ausgangsspannung von 5V wird mit 500mA belastet. Die Umgebungstemperatur sei 30°C. Der Spannungsregler wird mit Wärmeleitpaste auf dem Kühlkörper montiert, für diesen Wärmewiderstand wird 0,5 K/W angenommen. Welchen Wärmewiderstand darf der Kühlkörper höchstens haben, wenn als maximale Sperrschichttemperatur 110°C angenommen wird?

Diese Aufgabe kann so durchaus in der Praxis auftreten. Von den vielen Angaben darf man sich zunächst nicht verunsichern lassen. Wir verwenden das gezeigte thermische Ersatzschaltbild. Für die Rechnung benötigen wir außerdem noch den thermischen Widerstand [math]R_{th(jc)}[/math] aus dem Datenblatt.

Gegeben
[math]R_{th(jc)}=5 \frac{K}{W}[/math] (aus dem Datenblatt)

[math]R_{th(ch)}=0,5 \frac{K}{W}[/math]

[math]\vartheta_{j}=110°C[/math]

[math]\vartheta_{a}=30°C[/math]

[math]U_{ein}=12V[/math]

[math]U_{aus}=5V[/math]

[math]I=0,5A[/math]
Gesucht
[math]R_{th(ha)}[/math]
Rechnung
Zunächst muss die Verlustleistung am Regler berechnet werden. Diese beträgt

[math]P_V=P_{Ein}-P_{Aus}=12V \cdot 0,5A~-~5V \cdot 0,5A=3,5 W[/math].

Nun sind eigentlich auch schon alle Angaben vorhanden, sodass wir die Formel verwenden können.

[math]R_{th(ha)}=\frac{\vartheta_{j}-\vartheta_{a}}{P_{V}}-R_{th(jc)}-R_{th(ch)}[/math]

Einsetzen:

[math]R_{th(ha)}=\frac{110°C-30°C}{3,5W}-5\frac{K}{W}-0,5\frac{K}{W} \approx 17,4\frac{K}{W}[/math]
Ergebnis
Der Wärmewiderstand des Kühlkörpers darf maximal [math]17,4\frac{K}{W}[/math] betragen.
Zusatz
Aus dem Katalog wird ein Kühlkörper mit einem Wärmewiderstand von [math]10\frac{K}{W}[/math] gewählt. Welche Temperatur erreicht der Kühlkörper, wenn er bei den gegebenen Bedingungen eingesetzt wird?

[math]\vartheta_h=\vartheta_a+P_{V} \cdot R_{th(ha)}=30°C+3,5W \cdot 10 \frac{K}{W} \approx 65°C[/math]

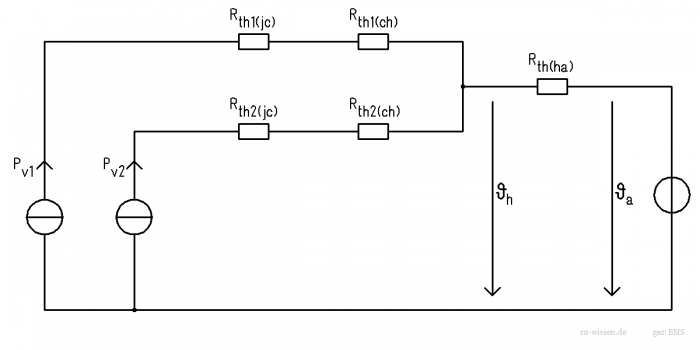
Mehrere Bauteile auf einem gemeinsamen Kühlkörper

Thermisches Ersatzschaltbild: zwei Wärmequellen, gemeinsamer Kühlkörper

Wird noch ausgebaut ...

Thermische Interface-Materialien (T.I.M.) und Montage

Wie bereits erwähnt, werden ICs in der Praxis nicht direkt auf einen Kühlkörper befestigt. Der Grund dafür ist folgender: Durch Unebenheiten und die rauhe Oberfläche von Kühlkörper und IC berühren sich die betreffenden Flächen unter dem Mikroskop gesehen nur minimal. Durch Lufteinschlüsse und die Tatsache, dass Luft ein schlechter Wärmeleiter ist, fällt in diesem Fall die thermische Anbindung des ICs an den Kühlkörper relativ schlecht aus.

Zum Ausgleich der Unebenheiten eignet sich Wärmeleitpaste, welche dünn auf die Kontaktfläche aufgetragen wird. Es genügt eine sehr geringe Menge der Wärmeleitpaste, die Schichtdicke liegt in der Größenordnung 0,1mm. Die Aufgabe der Wärmeleitpaste ist, die Unebenheiten der Kontaktflächen auszugleichen. Zu viel Wärmeleitpaste erhöht wiederum den thermischen Übergangswiderstand.

Ist zusätzlich eine elektrische Isolation zwischen IC und Kühlkörper erforderlich, können Glimmerscheiben (engl. mica) eingesetzt werden. Elektrische Isolation ist erforderlich, falls zum Beispiel mehrere Transistoren auf einen Kühlkörper montiert werden sollen und eine elektrische Verbindung der Kühlfahnen über den Kühlkörper zu Kurzschlüssen führen würde. Werden Glimmerscheiben verwendet, müssen diese beidseitig mit Wärmeleitpaste bestrichen werden, um sämtliche Unebenheiten auszugleichen. Die Glimmerscheiben werden zwischen IC und Kühlkörper eingebaut. Werden die ICs an den Kühlkörper geschraubt, muss auch die Schraube elektrisch isoliert werden. Hierfür sind entsprechende Hülsen aus Kunststoff erhältlich.

Wärmeleitfolien aus Silikon /Gap-Filler

BAUSTELLE

Zur Montage der ICs auf dem Kühlkörper gibt es mehrere Möglichkeiten. Üblich sind Schraubmontage oder die Verwendung von Metallclips aus Federstahl. Der Anpressdruck durch die Montage kann die thermische Kopplung des ICs zum Kühlkörper beeinflussen. Die Metallclips haben den Vorteil, dass der Anpressdruck mit der Zeit nicht nachlässt.

BAUSTELLE

Dynamisches Ersatzschaltbild

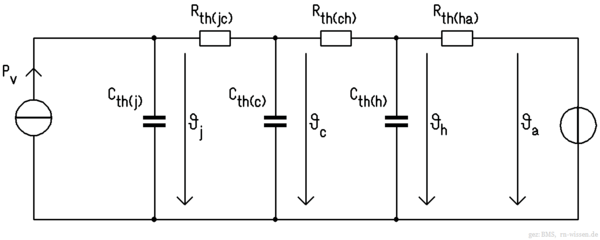
Bisher haben wir uns mit statischen Ersatzschaltbildern beschäftigt. Diese beinhalten die Wärmequellen, die Umgebungstemperatur sowie alle thermischen Widerstände. Nicht berücksichtigt wurden bislang Wärmekapazitäten. Erfahrungsgemäß dauert es eine gewissen Zeit, bis alle Gegenstände auf die berechnete Temperatur aufgeheizt sind. Um die zeitlichen Temperaturverläufe bestimmen zu können, müssen die thermischen Ersatzschaltbilder noch mit Wärmekapazitäten ergänzt werden. Wärmewiderstände und Wärmekapazitäten ergeben ein Tiefpassfilter mit einer definierten Zeitkonstante. Bei geeigneter Modellierung kommt das Modell kommt dem realen Temperaturverlauf schon sehr nahe. Nun können wir also zeitveränderliche Vorgänge modellieren. Dies ist insbesondere notwendig wenn sich stark ändernde Verlustleistungen (z.B. Impulsbelastung) an den Bauteilen auftreten und die Temperaturen vorab berechnet werden sollen. Im Hobbybereich ist diese Berechnung jedoch häufig nicht erforderlich, in der Regel genügt das statische Ersatzschaltbild.

Ergänzen wir das bisherige thermische Ersatzschaltbild um Wärmekapazitäten, ergibt sich das folgende thermische Ersatzschaltbild. Dieses Modell wird als Cauer-Typ bezeichnet. Wärmewiderstände und Wärmekapazitäten lassen sich physikalisch bestimmen und eindeutig im Ersatzschaltbild zuordnen. Berechnete Temperaturen entsprechen realen Temperaturen.

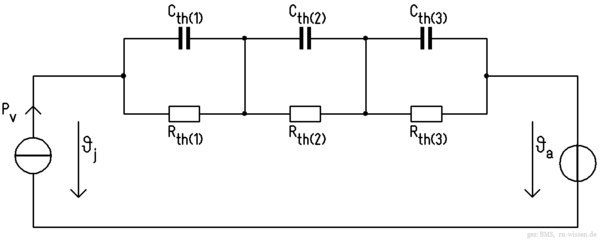
Den gleichen Sachverhalt kann man auch mit dem sogenannten Foster-Modell darstellen. Dieses Modell scheint weit verbreitet zu sein, ist allerdings nicht mehr besonders anschaulich. Die gezeigten Ersatzschaltbilder lassen sich auch ineinander überführen, allerdings unterscheiden sich die eingetragenen Wärmekapazitäten und Wärmewiderstände.

Die schwierige Aufgabe besteht nun darin, alle Zahlenwerte der Wärmewiderstände und Wärmekapazitäten zu bestimmen. Erst dann können die Temperaturverläufe in einer Simulation (z.B. mit SPICE) bestimmt werden. Im Hobbybereich ist diese Berechnung jedoch häufig nicht erforderlich.

Kühlkörperbauformen

Board-Level-Kühlkörper (aufsteckbare/aufklebbare Kühlkörper, auch für SMD, meist 1 Kühlkörper pro IC)
Strang-/Profilkühlkörper (meist für hohe Leistungen)
Kühlaggregate (Kanal + Lüfter)

Wozu eloxierte Oberflächen?

geringfügig höhere Wärmestrahlung (bei den niedrigen Temperaturen kaum ein Beitrag)
elektrische Isolation
Oberflächenschutz

Nachteile:

erhöhte Wärmeaufnahme aus der unmittelbaren Umgebung!

Stiftkühlkörper

hohe Oberfläche
bei dickem "Rücken"/"Boden" des Kühlkörpers gute Wärmespreizung
mit erzwungener Konvektion hohe Wärmeübertragung (quer zu den Stiften effektiver als in Stiftrichtung)
leichter und kompakter als Strangkühlkörper

todo

Lüfter

Lüfter werden vor allem dann eingesetzt, wenn der Kühlkörper bei rein passiver Kühlung zur groß, zu schwer oder zu teuer wird. Beim Einsatz des Lüfters führt die erzwungene Luftströmung zur besseren Wärmeabgabe an die Luft. Bei gleicher Temperatur kann der Kühlkörper dann kleiner gewählt werden. Bei hohen Leistungen sind der kleinere Kühlkörper mit Lüfter preisgünstiger und kompakter als ein großer, rein passiver Kühlkörper. Um welchen Faktor die Wärmeableitung mit Lüfter verbessert wird, hängt von vielen Parametern ab und kann nicht pauschal angegeben werden.

Vorteile

bessere Wärmeabgabe
Kühlkörper kann bei gleicher Temperatur kleiner, leichter und kostengünstiger werden
In kleinem Maßstab günstiger als Wasserkühlung o.ä.

Nachteile

zusätzlicher Stromverbrauch
Geräuschentwicklung und Vibrationen
zusätzliche Kosten für Lüfter und dessen Montage
Im Falle eines unbemerkten Ausfalls kann die Schaltung überhitzen (Abhilfe: Thermostat, Temperaturfühler oder Tachosignal auswerten)

Anordnungen:

Push-Prinzip: Der Lüfter bläst die Luft in den Kühlkörper/-kanal
Pull-Prinzip: Der Lüfter saugt die Luft aus dem Kühlkörper/-kanal heraus

Kenngrößen:

Luftdurchsatz in [math]\frac{m^{3}}{h}[/math]
Nennspannung, Nennstrom, Nennleistung
Typ Axial/Radial
Größe
Geräuschpegel
Art der Lagerung (Kugellager, Sinterbronze-Lager etc.)
Temperaturbereich
Lebensdauer, MTBF

Entwärmung auf einer Platine

Beim Leiterplattenentwurf muss bereits in der Designphase abgeschätzt werden, welche Verlustleistungen auftreten und wie die entstehende Wärme abgeführt werden kann. Die Anordnung der Bauteile und die Gestaltung der Leiterbahnen hat Auswirkungen auf das thermische Verhalten. Die Einbaulage der Platine kann die Entwärmung zudem beeinflussen. Erwärmte Umgebungsluft steigt bekanntlich nach oben und kann andere Komponenten oder Platinen aufheizen. Wird die Platine in ein Gehäuse eingebaut, müssen gegebenenfalls Lüftungsschlitze eingebracht werden oder die zu kühlenden Bauteile an der Gehäusewand platziert werden. Bei geschlossenen Gehäusen muss bei der Kühlkörperdimensionierung mit höheren Umgebungstemperaturen gerechnet werden (z.B. 50°C, 60°C), da sich die Wärme zunächst im Gehäuse staut und nur allmählich durch die Gehäusewand abgegeben wird.

Bedrahtete Bauteile

Für bedrahtete Bauteilgehäuse wie z.B. TO-220 sind zahlreiche Kühlkörpervarianten erhältlich. Für Printmontage eignen sich Kühlkörper, die mit Lötstiften oder Schrauben an der Platine befestigt werden. Das Bauteil selbst wird mit einem Federclip oder einer Schraube am Kühlkörper montiert. Die Größe, Bauform und Befestigung des Kühlkörpers muss bereits beim Leiterplattenentwurf berücksichtigt werden. Leistungsdioden und Leistungswiderstände sind in den meisten Fällen für Konvektionskühlung ausgelegt, d.h. durch Luftströmung. Diese werden meist mit etwas Abstand von der Platinenoberfläche montiert, um die gesamte Bauteiloberfläche zur Kühlung nutzen zu können und um die Platine nicht unnötig aufzuheizen.

Zur Verbesserung der Wärmeableitung kann, abgesehen vom Kühlkörper, auch die Platine bei der Wärmeverteilung helfen:

Breite Leiterbahnen können Wärme abführen und auf eine große Fläche verteilen
Eine dickere Kupferkaschierung kann die Wärmeableitung unterstützen (Standard sind 35µm, erhältlich sind auch 70µm und mehr), dies reduziert zudem die elektrischen Leiterbahnwiderstände
Mit einer großen Zahl von Durchkontaktierungen (vias) kann die Wärme auf andere Kupferlagen verteilt werden (der Platinenkern FR4 allein hat eine schlechte Wärmeleitfähigkeit)
Einsatz spezieller Platinenmaterialien (Alukern) z.B. bei Platinen für High-Power-LEDs
Für kleinere ICs mit Wärmeentwicklung eignen sich aufklebbare Kühlkörper

Beim Entwurf der Platine muss den Bauteilen in der Nähe der Wärmequelle besondere Aufmerksamkeit geschenkt werden. Vor allem sind Elektrolytkondensatoren (Elkos) betroffen, da diese durch benachbarte Wärmequellen allmählich austrocknen und zum Ausfall der Schaltung führen können! Elkos sollten möglichst so platziert werden, dass sie eine geringe Temperatur und somit eine hohe Lebensdauer erreichen. Jedoch ist dies bei manchen Anwendungen nur eingeschränkt möglich. Beispielsweise sind bei Schaltreglern kurze Leiterschleifen erwünscht, um die elektromagnetische Verträglichkeit zu verbessern (Leiterschleifen wirken als Antenne) und um parasitäre Induktivitäten und Widerstände zu reduzieren. Der Einsatz hochwertiger Elkos mit geringem ESR, hoher Maximaltemperatur und Lebensdauer ist empfehlenswert. Zudem ist auf ausreichende Spannungsfestigkeit und geringe Rippleströme im Betrieb zu achten. Im Laufe der Betriebszeit sinkt die Kapazität des Elkos und die Verluste steigen. Die Lebensdauer der Elkos kann abgeschätzt werden. Die Hersteller geben idR. die Lebensdauer bei der spezifizierten Maximaltemperatur an, z.B. 5000h bei 105°C. Zur Abschätzung der Lebensdauer gilt hier auch die 10°C-Regel (laut Panasonic im Bereich 40°C bis 100°C), d.h. pro 10°C niedrigerer Betriebstemperatur verdoppelt sich die Lebensdauer des Elkos. Die erwartete Lebensdauer kann mit der folgenden Formel (Panasonic) abgeschätzt werden:

[math]\Large L=L_{Tmax} \cdot 2^{\left( \frac{T_{max} - T}{10} \right)}[/math]

Beispiel

Ein Elko ist mit 5000h bei 105°C spezifiziert. Welche Lebensdauer wird bei einer Temperatur von 55°C erwartet?

Gegeben: [math]\large L_{Tmax}=5000h[/math] , [math]\large T_{max}=105°C[/math] , [math]\large T=55°C[/math]
Rechnung: [math]\large L=L_{Tmax} \cdot 2^{\left( \frac{T_{max} - T}{10} \right)}=5000h \cdot 2^{\left( \frac{105°C - 55°C}{10} \right)}=5000h \cdot 2^5=5000h \cdot 32=160000h[/math]
Ergebnis: Die Lebensdauer des Elkos beträgt unter diesen Bedingungen etwa 160000h, also über 18 Jahre Dauerbetrieb!
Bemerkung: Würde man z.B. einen billigen 2000h/85°C-Elko verwenden, würde dieser unter den gleichen Bedingungen keine 2 Jahre durchhalten!

Liegt das Datenblatt des verwendeten Elkos vor, sollte man sich an die dort genannten Berechnungen und Zahlenwerte halten. Die gezeigte Berechnung ist nur eine Näherungsformel. Für weitere Verwendungshinweise sei auf die Application Guidelines für Radial Lead Type Aluminum Electrolytic Capacitors von Panasonic verwiesen (siehe Quellenangaben und Verweise am Seitenende).

SMD-Bauteile

SMD-Bauteile können meist über die Platine gut entwärmt werden. Dies ist normalerweise nur bei geringen Verlustleistungen möglich. Die Abwärme der Bauteile muss auf eine möglichst große Fläche verteilt werden, durch große Kupferflächen auf der Platine kann dies erreicht werden. Da die Wärmeleitfähigkeit der Kupferauflage deutlich höher ist als die Wärmeleitfähigkeit des Platinenmaterials FR4, wird sich die Wärme hauptsächlich in der Fläche verteilen, jedoch weniger durch die Platine hindurch. Um die Wärmeleitung durch die Platine (z.B. von Ober- zu Unterseite) zu erhöhen, müssen Durchkontaktierungen gesetzt werden. Sogenannte "Thermal Vias" werden in einer großen Anzahl an das zu entwärmende Bauteil gesetzt und können damit die Wärme zu anderen Kupferlagen der Platine weiterleiten. Die Wärmeleitung durch die Platine hindurch wird verbessert, liegt aber dennoch deutlich unter der Wärmeleitfähigkeit von reinem Kupfer. Thermische Vias können aufgrund ihrer kleinen Masse kaum einen Beitrag zur gesamten "Kühlmasse" beitragen. Ob schließlich eine Entwärmung durch die Platine ausreicht, muss durch Simulation oder Messung gezeigt werden.

Welche Temperatur das Bauteil auf der Platine erreicht, kann nach dem Aufbau natürlich gemessen werden. Besser wäre es jedoch, die Temperaturen bereits beim Entwurf der Platine zu kennen, um einschätzen zu können, ob die Entwärmung ausreichend ist. Allgemeine Angaben hierfür sind schwer zu finden, jedoch gibt es vereinzelt Angaben in Datenblättern von Halbleitern zur Entwärmung. An den folgenden Zahlenwerten kann man sich orientieren, wenn man ähnliche Bauteile entwärmen möchte. Damit man für die genannten Flächen eine grobe Vorstellung hat, sei noch erwähnt: ein Cent hat eine Fläche von grob [math]200mm^2[/math], ein Euro hat grob [math]400mm^2[/math].

Für SMD-Bauteile exisitieren Kühlkörper, die sich direkt auf die Platine löten lassen, diese sind auch maschinenbestückbar.

TO263 (=D2PAK)

Im Datenblatt des Schaltreglers LM2576 von National Semiconductor findet man für das TO263-Gehäuse einige Angaben. Das TO263-Gehäuse gleicht übrigens dem TO220 bis auf die Tatsache, dass die Kühlfahne kürzer ist und das Gehäuse für SMD-Montage vorgesehen ist. Das Datenblatt gibt thermische Widerstände für den Übergang Junction-Ambient an. Die Angabe ist abhängig von der Kupferfläche auf der Platine, die unmittelbar für das Bauteil aus Kühlkörper wirkt. Die Zahlenwerte aus dem Datenblatt wurden in Quadratmillimeter umgerechnet, gerundet und stehen nun in der Tabelle bereit. Keine Angaben macht der Hersteller zu den Rahmenbedingungen, unter denen die thermischen Widerstände ermittelt wurden (Platinendicke, Durchkontaktierungen, Form der Kupferfläche und Dicke der Kupferkaschierung). Dennoch können die Werte zur groben Orientierung dienen.

Kupferfläche	therm. Widerstand
[math]325 mm^2[/math]	[math]R_{th(ja)}\approx 50\frac{K}{W} [/math]
[math]645 mm^2[/math]	[math]R_{th(ja)}\approx 37\frac{K}{W} [/math]
[math]1030 mm^2[/math]	[math]R_{th(ja)}\approx 32\frac{K}{W} [/math]

TO252 (=DPAK), SOT223

Im Datenblatt des Low-Drop-Spannungsreglers LM1117 von National Semiconductor sind Angaben zur Entwärmung über die Platine von SOT223 und TO252-Gehäusen vorhanden. Der Hersteller gibt an, für das SOT223-Gehäuse eine 35µm dicke, und für das TO252-Gehäuse eine 70µm dicke Kupferkaschierung der Platine verwendet zu haben. Leider finden sich in diesem Datenblatt keine Informationen zu Durchkontaktierungen, Platinendicke, und ob das IC auf der Ober- oder Unterseite der Platine montiert wurde (Vermutung: oben montiert, da angegebene thermische Widerstände geringer sind). Der Hersteller hat drei Fälle untersucht: Kupferfläche oben, Kupferfläche unten, Kupferfläche beidseitig. Für das thermische Platinendesign kann man diese Zahlenwerte zumindest als Richtwerte verwenden. Das Datenblatt enthält zudem Zeichnungen der Kühlflächen. Die Zahlenwerte wurden wieder in Quadratmillimeter umgerechnet und gerundet und in die folgenden Tabelle eingetragen:

Kupferfläche top	Kupferfläche bottom	therm. Widerstand SOT223	therm. Widerstand TO252
[math] 200mm^2[/math]	-	[math]R_{th(ja)}\approx 84\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 60\frac{K}{W} [/math]
[math] 350mm^2[/math]	-	[math]R_{th(ja)}\approx 75\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 54\frac{K}{W} [/math]
[math] 650mm^2[/math]	-	[math]R_{th(ja)}\approx 66\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 47\frac{K}{W} [/math]
-	[math] 250mm^2[/math]	[math]R_{th(ja)}\approx 98\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 70\frac{K}{W} [/math]
-	[math] 400mm^2[/math]	[math]R_{th(ja)}\approx 89\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 63\frac{K}{W} [/math]
-	[math] 650mm^2[/math]	[math]R_{th(ja)}\approx 79\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 57\frac{K}{W} [/math]
[math] 200mm^2[/math]	[math] 200mm^2[/math]	[math]R_{th(ja)}\approx 83\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 61\frac{K}{W} [/math]
[math] 250mm^2[/math]	[math] 250mm^2[/math]	[math]R_{th(ja)}\approx 75\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 55\frac{K}{W} [/math]
[math] 350mm^2[/math]	[math] 350mm^2[/math]	[math]R_{th(ja)}\approx 70\frac{K}{W}[/math]	[math]R_{th(ja)}\approx 53\frac{K}{W} [/math]

SO8

Für das SO8-Gehäuse findet man eine Angabe im Datenblatt des Spannungsreglers 78L05 von ST:

Kupferfläche	therm. Widerstand
[math]600 mm^2[/math]	[math]R_{th(ja)}\approx 55\frac{K}{W} [/math]

SO20

Aus dem Datenblatt des L293DD sind Angaben zum SO20-Gehäuse enthalten. In diesem Falle sind 8 zentrale Pins an die Kühlfläche angebunden, die Kupferkaschierung ist vermutlich einseitig 35µm. Die groben Richtwerte sind:

Kupferfläche	therm. Widerstand
[math]200 mm^2[/math]	[math]R_{th(ja)}\approx 60\frac{K}{W} [/math]
[math]400 mm^2[/math]	[math]R_{th(ja)}\approx 53\frac{K}{W} [/math]
[math]600 mm^2[/math]	[math]R_{th(ja)}\approx 51\frac{K}{W} [/math]
[math]800 mm^2[/math]	[math]R_{th(ja)}\approx 50\frac{K}{W} [/math]

PowerDIP20

Für das DIP20-Gehäuse wird man im Datenblatt des Motortreibers L6202 von ST fündig. Bei 35µm Kupferkaschierung der Platine ergeben sich die folgenden thermischen Widerstände.

Kupferfläche	therm. Widerstand
[math]0 mm^2[/math]	[math]R_{th(ja)}\approx 58\frac{K}{W} [/math]
[math]200 mm^2[/math]	[math]R_{th(ja)}\approx 45\frac{K}{W} [/math]
[math]400 mm^2[/math]	[math]R_{th(ja)}\approx 39\frac{K}{W} [/math]
[math]600 mm^2[/math]	[math]R_{th(ja)}\approx 38\frac{K}{W} [/math]
[math]800 mm^2[/math]	[math]R_{th(ja)}\approx 37\frac{K}{W} [/math]

Für die Form der empfohlenen Kühlfläche sei auf das Datenblatt verwiesen. Wird das IC in einem Sockel verwendet, muss man sicherlich von höheren thermischen Widerständen ausgehen.

AN-994

In der Application Note AN-994 - Maximizing the Effectiveness of your SMD Assemblies von International Rectifier (IRF) sind weitere Daten vorhanden. Die dort genannten Daten sind jedoch teils drastisch niedriger als die hier genannten. Eine mögliche Erklärung sind z.B. die höhere Kupferauflage (70µm) oder evtl. optimierte Wärmewiderstände innerhalb der Gehäuse.

Große Kupferflächen

Im Application Hint 17 - Designing P.C. Board Heat Sinks - by Bob Wolbert (Micrel) werden Angaben zu thermischen Widerständen der Platine für vergleichsweise große Flächen gemacht. Die thermischen Widerstände beschreiben den Übergang [math]R_{th(ha)}[/math] unter den Bedingungen: Quadratische Kupferfläche, einseitig, horizontal montiert, Lötstopplack, keine Belüftung. Die Dicke der Kupferkaschierung ist nicht angegeben. Hier einige Werte, abgelesen aus dem Diagramm der genannten Application Note:

Kupferfläche	therm. Widerstand
[math]500 mm^2[/math]	[math]R_{th(ha)}\approx 60\frac{K}{W} [/math]
[math]1000 mm^2[/math]	[math]R_{th(ha)}\approx 45\frac{K}{W} [/math]
[math]1500 mm^2[/math]	[math]R_{th(ha)}\approx 38\frac{K}{W} [/math]
[math]2000 mm^2[/math]	[math]R_{th(ha)}\approx 33\frac{K}{W} [/math]
[math]2500 mm^2[/math]	[math]R_{th(ha)}\approx 30\frac{K}{W} [/math]
[math]3000 mm^2[/math]	[math]R_{th(ha)}\approx 28\frac{K}{W} [/math]
[math]4000 mm^2[/math]	[math]R_{th(ha)}\approx 24\frac{K}{W} [/math]
[math]5000 mm^2[/math]	[math]R_{th(ha)}\approx 22\frac{K}{W} [/math]

Abschlusskommentar

An den gezeigten, thermischen Widerständen sieht man leicht: je größer die Kühlfläche, desto geringer der thermische Widerstand. Dieses Verhalten würde man so auch erwarten.

Ab einer bestimmten Fläche wird die Platine als Kühlkörper jedoch unhandlich, und man wird die Fläche nicht weiter vergrößern. Die mit den Kupferflächen erreichten thermischen Widerstände sind für viele Anwendungen noch deutlich zu hoch. Bei Verlustleistungen von wenigen Watt werden dadurch bereits kritische Chiptemperaturen erreicht. Wie bereits oben erwähnt, funktioniert die Entwärmung von SMD-Komponenten über die Platine also nur für kleine Verlustleistungen. Bei größeren Verlustleistungen müssen zusätzliche Entwärmungsmaßnahmen getroffen werden (z.B. aufklebbarer Kühlkörper, etc.). Zielführend ist auch, die Ursache der Erwärmung, nämlich die Verlustleistung zu verringern. Wird beispielsweise ein Linearregler durch einen effizienteren Schaltregler ersetzt, kann die Entwärmung aufgrund der kleineren Verlustleistung deutlich einfacher gestaltet werden. Ob die Verringerung der Verlustleistung möglich ist, hängt natürlich von der Anwendung ab.

Spezielle Kühlkörper

todo

Autoren

BMS

Quellen und Verweise

Printmedien:

Best, Siegfried W.: Elektronikkühlung und Wärmemanagement von A bis Z. In: Elektronikpraxis - Sonderheft Elektromechanik, April 2013. S. 20ff.
Best, Tobias: Thermisches Via, die kleine Schwester der Heatpipe. In: Elektronikpraxis, April 2013. S. 12ff.
Erdmann, Marc: Beste Effizienz auch beim Thermal Management. In: Elektronikpraxis - Sonderheft Leistungelektronik und Stromversorgung. März 2015. S. 38ff.
Kerstin, Nils; Schulz, Martin: Thermische Widerstände genau messen - eine Herausforderung. In: Elektronikpraxis, Nr. 17, September 2014. S. 48ff.
K.R. (Alutronic): Stiftkühlkörper für die Leistungselektronik. In: Elektronikpraxis Nr.9, Mai 2014. S. 50ff.
Harpain, Jürgen: Wärmeleitmaterial kompensiert Lufteinschlüsse. In: Elektronikpraxis Nr.1, Januar 2014. S. 36ff.
Harpain, Jürgen: Entwärmungskonzepte für Einzelhalbleiter und ICs. In: Elektronikpraxis - Sonderheft Elektromechanik, April 2014. S. 14ff.
Schulz, Martin: Fünf Fettnäpfchen beim Bestimmen thermischer Größen. In: Elektronikpraxis, November 2013. S. 36ff.
Schulz, Martin: Mythen und Legenden über Wärmeleitmaterialien. In: Elektronikpraxis Nr.2., Januar 2014. S. 42ff.
Specovius, J.: Grundkurs Leistungselektronik: Bauelemente, Schaltungen und Systeme. Wiesbaden 2014. 6. Auflage. S.95-104

Datenblätter, aus denen thermische Widerstände entnommen wurden:

Weblinks:

Kühlkörper

Ansichten

Inhaltsverzeichnis

Einleitung

Wärmeübertragung

Materialien

Definitionen

Statisches Ersatzschaltbild

Bauteil ohne Kühlkörper

Derating

Beispielrechnung

Bauteil mit Kühlkörper und T.I.M.

Beispielrechnung

Mehrere Bauteile auf einem gemeinsamen Kühlkörper

Thermische Interface-Materialien (T.I.M.) und Montage

Dynamisches Ersatzschaltbild

Kühlkörperbauformen

Lüfter

Entwärmung auf einer Platine

Bedrahtete Bauteile

SMD-Bauteile

Spezielle Kühlkörper

Autoren

Quellen und Verweise

Navigationsmenü

Hauptthemen

Navigation

Suche

Werkzeuge

Meine Werkzeuge