Gelegentlich ist es nötig, eine nichtlineare Kennlinie eines Sensors in eine Funktion zu übertragen, um aus dem Ausgangssignal die gemessene Größe berechnnen zu können. Ein dazu geeignetes Werkzeug ist gnuplot. Gnuplot ist ein frei verfügbares Programm, um unter Windows, Linux, Unix, Dos, usw. Messwerte oder Funktionswerte darzustellen. Das Vorgehen wird am Beispiel des Standardsensors Sharp GP2D120 demonstriert.
Dazu ist es zuerst nötig, die Kennlinie zu vermessen und in eine Textdatei zu speichern. (Alternativ kann man aus Tabellenkakulationspogrammen eine .csv-Datei exportieren und als Feldtrennzeichen den Tabulator auswählen.) Hier das Ergebnis von 15 Minuten mit Maßband und Multimeter, linke Spalte Spannung in V, rechte Spalte Entfernung in mm.
3.00 40 2.89 50 2.44 60 2.04 70 1.81 80 1.56 90 1.45 100 1.32 110 1.16 120 1.09 130 0.99 140 0.94 150 0.85 160 0.81 170 0.78 180 0.74 190 0.68 200 0.6 210 0.6 220 0.54 230 0.5 240 0.48 250 0.45 260 0.43 270 0.41 280 0.39 290 0.39 300 0.37 310
Diese Daten z. B. in Messung.txt speichern (als Dezimaltrennzeichen den Punkt benutzen) und im gleichen Verzeichnis gnuplot starten (oder unter Windows mit ChDir in das Verzeichnis mit Messung.txt wechseln):
gnuplot>
Mit
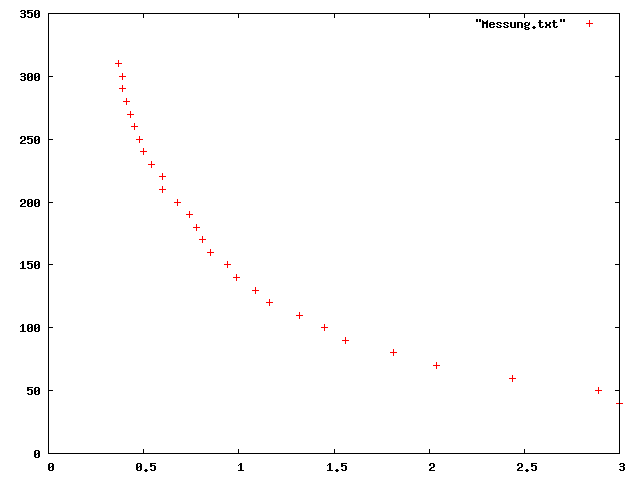
gnuplot> plot "Messung.txt"
erscheint ein Fenster mit den Messwerten:
Als nächstes muss man eine Funktion finden, die die Kurve nachbilden könnte. Wenn die Berechnung später auf einem Mikrocontroller geschehen soll, ist es sinnvoll, dazu eine möglichst effizient zu berechnende Funktion auszuwählen. Grundsätzlich sieht die Kurve nach einer 1/x-Funktion aus, was gnuplot mitgeteilt werden muss:
gnuplot> f(x) = a / (x)
Jetzt kann mit
gnuplot> fit f(x) "Messung.txt" via a
der Parameter a bestimmt werden, mit dem f(x) den Messdaten am besten entspricht. Das Ergebnis lässt sich mit
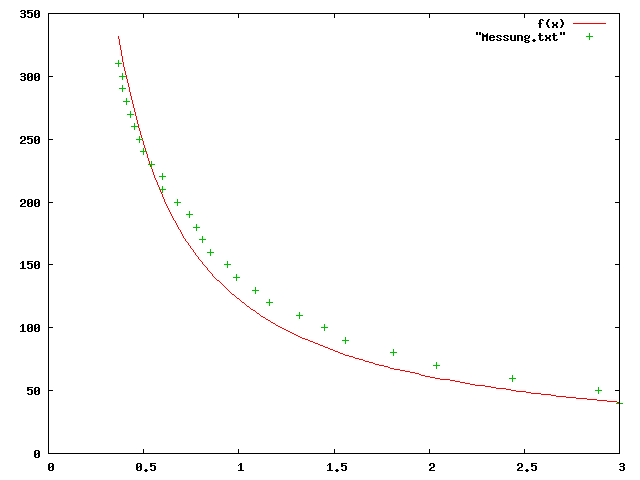
gnuplot> plot "Messung.txt", f(x) with lines
betrachten.
In diesem Fall passt es noch nicht so ganz, also scheint die Funktion etwas komplizierter zu sein. Nächster Versuch:
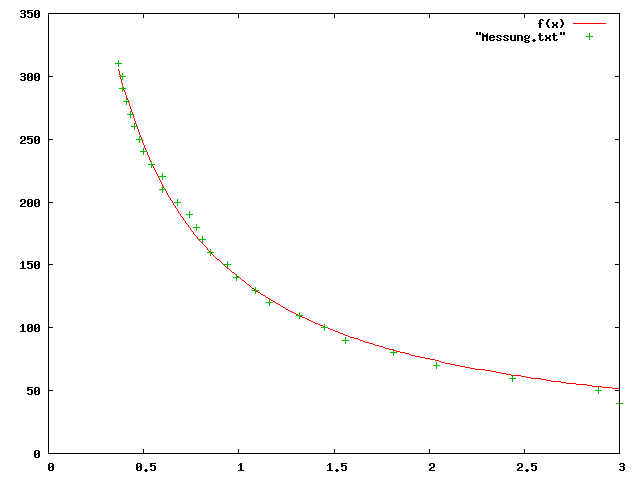
gnuplot> f(x) = a / (x+b) gnuplot> fit f(x) "Messdaten.txt" via a,b gnuplot> plot "Messung.txt", f(x) with lines
Das Ergebnis sieht ausreichend genau aus. Wenn man im Konsolenfenster etwas hochscrollt, findet man die Parameter a und b wieder:
Final set of parameters Asymptotic Standard Error ======================= ========================== a = 162.436 +/- 3.165 (1.948%) b = 0.162385 +/- 0.01297 (7.985%)
Die Entfernung in Milimetern lässt sich also mit der Formel
Entfernung = 162.4 / (Spannung + 0.1624)
aus der Spannung in Volt berechnen.