Dieser Artikel beschäftigt sich mit der Optischen Drehzahlmessung mit Hilfe einer Lochscheibe und Gabellichtschranke berechnet über die
Winkelgeschwindigkeit ohne Drehrichtungserkennung.
Einführung
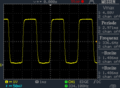
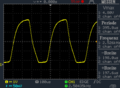
Die Winkelgeschwindigkeit ist die Winkeländerung pro Zeiteinheit. Mit der Lichtschranke und den geometrischen Daten der Lochscheibe kann man nun relativ einfach die Zeit für eine bestimmte Winkeländerung messen. Die Lochscheibe gibt uns die Winkeländerung bei einer Periode vor, bei einer 32er Lochscheibe wären das 11,25° pro Periode , wie in den Bildern vom Oszilloskop zu sehen ändert sich natürlich bei Änderung der Drehzahl die Periodendauer, die Winkeländerung pro Periode ist aber konstant da diese durch die Lochscheibe vor gegeben ist.
Um die Periodendauer zu messen verwende ich den ICP1 (Input Capture Pin) eines Atmega8 der bei steigender Flanke den Timer1 ausliest und in das ICR1 Register schreibt. Läuft der Mikrocontroller auf 8Mhz und wir stellen den Vorteiler des Timers auf 8 so bekommen wir die Periodendauer in µs als Wert.
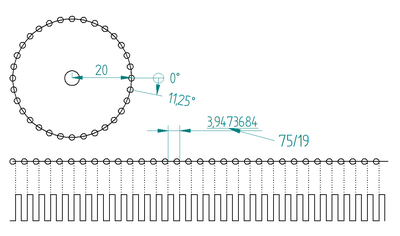
Auslegen der Lochscheibe
In den meisten fällen definiert der mechanische Aufbau den Durchmesser der Lochscheibe und die Drehzahl die Anzahl der Löcher. Wenn man das Drehzahlband abschätzen kann ist es hilfreich sich schon Gedanken um die Programmierung zu machen, denn bei hohen Drehzahlen springt der µC jedes mal in die Interrupt Service Routine rein wenn man es so programmiert wie im Beispiel. Bei hohen Drehzahlen sollte die Auflösung somit gröber sein, bei niedriger feiner.
Berechnungen
Hier folgt nun die Berechnung über die Periodendauer, beachten sollte man das im Bogenmaß gerechnet wird, ein Winkel mit dem Bogenmaß 1 rad hat ein Gradmaß von ca. 57,3°. 11.25° sind also ca. 0,196 rad, das führt später natürlich zu unschönen Rechenoperationen im µC, Stichwort Festkommaarithmetik.
Nach dem umstellen kommt man aber auf eine recht handliche Formel [math]\sqrt{5}[/math]

|
An diesem Artikel arbeitet gerade Mitglied the_muck.
Am besten momentan noch keine gravierenden Ergänzungen / Änderungen vornehmen. Dieser Hinweis verschwindet wenn der Autor soweit ist. Sollte dieser Hinweis länger als drei Tage auf einer Seite sein, bitte beim Autor the_muck per PM / Mail oder Forum nachfragen ob er vergessen wurde. |