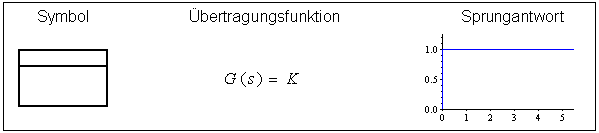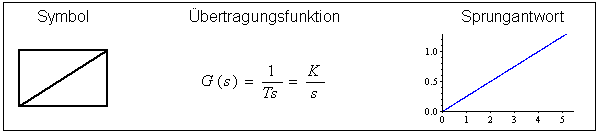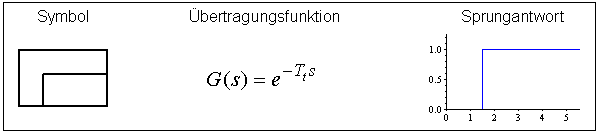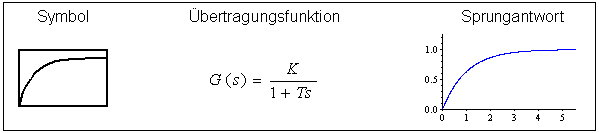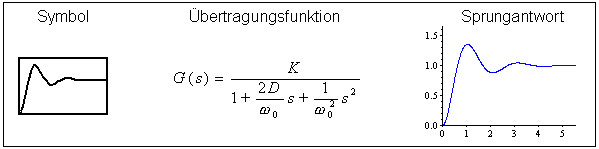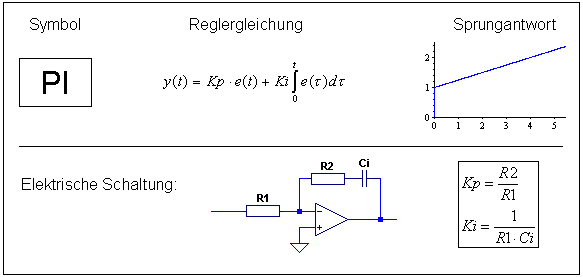Regelungen sind ein Bestandteil unseres Lebens und das nicht nur seit Erfindung der Dampfmaschine.
Allein schon der aufrechte Gang funktioniert nur mit Regelung. Dabei wirken die Sinne als Sensoren, das Gehirn als Regler und die Muskeln als Aktuatoren. Weitere Regelungen in unserem Körper sind z.B. die Konstanthaltung der Körpertemperatur, der Blutdruck, die Anpassung der Pupille auf Helligkeitsänderungen usw.
Im technischen Zeitalter ist der erste geschichtlich bedeutende Regler der Fliehkraftregler von James Watt, der für die Drehzahlregelung seiner Dampfmaschine eingesetzt wurde. Seitdem ist die Regelungstechnik aus keinem Technikbereich mehr wegzudenken. Die Regelungstechnik begegnet uns im täglichen Leben auf Schritt und Tritt: Der Temperaturregler der Zentralheizung, der Temperaturregler des Kühlschranks, der Regler für die Belichtungsautomatik im Fotoapparat, das ABS-System im Auto und die Netzspannungs- und Frequenzregelung des europäischen Versorgungsnetzes sind nur einige wenige Beispiele aus diesem Bereich.
Autor Waste
Inhaltsverzeichnis
- 1 Einleitung
- 2 Der Regelkreis
- 3 Die Regelstrecke
- 4 Der Regler
- 5 Vergleich der Reglertypen
- 6 Digitaler Regler
- 7 Dimensionierung des Reglers
- 8 Hilfsprogramme zur Analyse und Optimierung
- 9 Modellierung eines Motors/Antriebs
- 10 Beispiel: Drehzahlregelung
- 11 Beispiel: Lageregelung
- 12 Autoren
- 13 Siehe auch
- 14 External links
Einleitung
Der Begriff Regelung ist zu unterscheiden von dem im allgemeinen Sprachgebrauch oft synonym gebrauchten Begriff der Steuerung. Das Steuern ist ein rein vorwärts gerichteter Prozess ohne Rückkopplung. Die Ausgangsgröße wird dabei nicht überwacht und kann sich durch Störungen von außen verändern. Ein Beispiel ist die Steuerung eines Motors mit einer einstellbaren Spannung. Durch Laständerungen wird sich die Drehzahl des Motors ändern. Soll nun die Drehzahl konstant gehalten werden, bedarf es einer Rückkopplung um über die Spannung die Drehzahl anzupassen. Diese Rückkopplung ist das Kennzeichen einer Regelung.
Das Regeln ist ein Vorgang, bei dem die Ausgangsgröße, im Beispiel die Drehzahl, fortlaufend überwacht wird und bei Abweichung über die Stellgröße, im Beispiel die Spannung, korrigiert wird. Der sich dabei ergebende Wirkungsablauf findet in einem geschlossenen Kreis, dem Regelkreis, statt.
Der Regelkreis
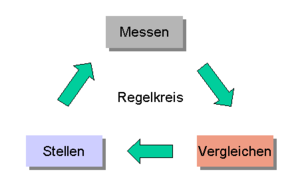
Das Prinzip einer Regelung ist das fortlaufende: Messen – Vergleichen – Stellen
- Messen
- Die Regelgröße wird direkt oder mittels Sensoren gemessen.
- Vergleichen
- Der Wert der Regelgröße wird mit dem Sollwert verglichen. Die Differenz ist die Regelabweichung.
- Stellen
- Aus der Regelabweichung wird unter Berücksichtigung der dynamischen Eigenschaften der Regelstrecke die Stellgröße bestimmt.
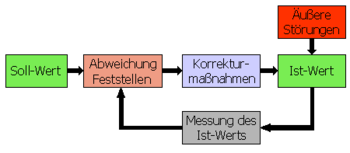
Ein Regelkreis dient dazu, eine vorgegebene physikalische Größe, die Regelgröße, auf einen gewünschten Wert (Sollwert) zu bringen und dort zu halten, unabhängig von eventuell auftretenden Störungen. Um die Regelungsaufgabe zu erfüllen, muss der Augenblickswert der Regelgröße – der Istwert – gemessen und mit dem Sollwert verglichen werden. Bei auftretenden Abweichungen muss in geeigneter Art und Weise nachgestellt werden.
Um nun diese Aufgabe technisch zu lösen, gibt es die Regelungstechnik. Sie baut im wesentlichen auf die mathematische Beschreibung und Modellbildung des Systems Regelkreis. Zur Modellierung, Beschreibung und Simulation werden Blockschaltbilder mit diskreten Signalgliedern verwendet.
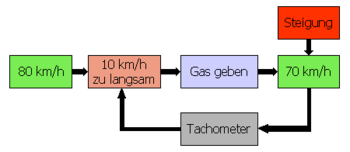
Ein typisches Beispiel für einen Regelkreis – eine Geschwindigkeitsregelung – wird im nebenstehenden Bild gezeigt. Die Sollgeschwindigkeit ist 80 km/h. Durch eine äußere Störung, in dem Fall eine Steigung, verlangsamt sich das Fahrzeug auf 70 km/h. Die Abweichung wird durch das Tachometer erfasst. Als Korrekturmaßnahme wird mehr Gas gegeben, um wieder auf die Sollgeschwindigkeit von 80 km/h zu kommen.
Begriffe
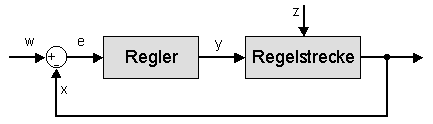
Ein Regelkreis besteht entsprechend des vereinfachten Blockschaltbildes, wie es oft in der Regelungstechnik verwendet wird, aus den Hauptteilen Regler und Regelstrecke:
- Regler
- Ist der Teil des Regelkreises, der unter Berücksichtigung der dynamischen Eigenschaften der Regelstrecke aus der Regelabweichung die Korrekturmaßnahmen zum Ausregeln ergreift.
- Regelstrecke
- Ist der Teil des Regelkreises, der vom Regler ausgeregelt werden soll.
- Führungsgröße (Sollwert) w
- Vorgegebener Wert, auf dem die Regelgröße durch die Regelung gehalten werden soll. Sie ist eine von der Regelung nicht beeinflusste Größe und wird von außen zugeführt.
- Regelgröße (Istwert) x
- Ist die Ausgangsgröße der Regelstrecke, die zum Zweck des Regelns erfasst und zum Vergleich rückgeführt wird. In vielen Fällen ist in der Rückführung noch eine Messeinrichtung (Sensor) gezeichnet, die den Istwert erfasst, hier der Einfachheit halber weggelassen.
- Regelabweichung e
- Differenz zwischen Führungsgröße und Regelgröße e = w – x, bildet die eigentliche Eingangsgröße des Reglers.
- Stellgröße y
- Ausgangsgröße der Regeleinrichtung und zugleich Eingangsgröße der Strecke. Sie überträgt die steuernde Wirkung des Reglers auf die Strecke.
- Störgröße z
- Eine von außen wirkende Größe, die eine Änderung des Istwertes der Regelgröße bewirkt und einen Regelvorgang auslöst.
Die Regelstrecke
Die Regelstrecke stellt den zu regelnden Teil bzw. den zu regelnden Prozess dar und umfasst normalerweise eine Reihe von einzelnen Gliedern. Die Glieder werden entsprechend ihrem Zeitverhalten charakterisiert. Um das Zeitverhalten herauszufinden, legt man an den Eingang ein Testsignal an und zeichnet die Antwort auf. Im einfachsten Fall wird der Eingang mit einer sprunghaften Änderung beaufschlagt. Die Antwort auf die sprunghafte Änderung der Eingangsgröße wird Sprungantwort genannt und gibt Aufschluss über die Art der Regelstrecke und kann eventuell bereits genutzt werden, um die Parameter der Regelstrecke zu bestimmen.
Für den Aufbau eines gut funktionierenden Regelkreises und die Auslegung von Reglern ist es eine Voraussetzung zu wissen, wie die Regelstrecke reagiert. Ohne ein genaues Wissen um das dynamische Verhalten der Regelstrecke ist es nicht möglich geeignete Regler auszuwählen und diese zu parametrieren.
Die wichtigsten dynamischen Grundelemente zur Charakterisierung der Regelstrecke sind nachfolgend aufgelistet. Jedes Element wird mit einem Block dargestellt und darin durch ein Symbol oder der stilisierten Sprungantwort gekennzeichnet.
Proportionalglied (P-Glied)
Die einfachste Art einer Regelstrecke.
- Beispiele
- Hebel, Getriebe, Verstärker, Spannungsteiler, Sensoren bei denen das Zeitverhalten vernachlässigt werden kann
Integrator (I-Glied)
Strecke ohne Ausgleich, ist häufig in Regelstrecken vorhanden.
- Beispiele
- Beschleunigung → Geschwindigkeit → Weg, Strom → Kondensatorspannung
Verzögerungsglied 0.Ordnung (Totzeitglied)
Entsteht durch Laufzeiten von Material oder Signalen. Je größer die Verzögerungszeit einer Regelstrecke ist, um so schwieriger ist sie zu regeln.
- Beispiele
- Förderband, Rechenzeit, A/D-Wandler
Nicht zu verwechseln mit der Totzeit, die durch das asynchrone Auftreten eines Ereignisses auf einen Zyklus entsteht. Vom Verzögerungsglied 0.Ordnung unterscheidet sich diese dadurch, daß sie mit einer gleichverteilten Wahrscheinlichkeit zwischen "gar nicht" und dem gesamten Umfang auftritt. Diese Totzeit ist mechanisch mit einem Spiel vergleichbar das "gar nicht" bis zum vollen Umfang zu einem Fehler beiträgt.
- Beispiele
- Erkennen eines Signals an einem Mikroprozessor
Verzögerungsglied 1.Ordnung (PT1-Glied)
Viele einfache Regelstrecken haben ein solches Verhalten bzw. können näherungsweise damit beschrieben werden. Ist ein P-Glied mit nicht vernachlässigbarem Zeitverhalten.
- Beispiele
- Gleichstrommotor (Spannung → Drehzahl), näherungsweise; Widerstand-Kondensator-Schaltung (RC-Glied)
Verzögerungsglied 2.Ordnung (PT2-Glied)
Man unterscheidet schwingungsfähige und nicht schwingungsfähige PT2-Glieder. Zur Charakterisierung gibt es die Parameter Dämpfung D und Eckfrequenz w0 oder die Zeitkonstanten T1 und T2. Für Dämpfung D<1 ist es schwingungsfähig.
- Beispiele
- Mechanischer Schwinger (Feder-Masse-System), elektrischer Schwingkreis (RLC-Kreis)
Nicht schwingfähiges PT2-Glied:
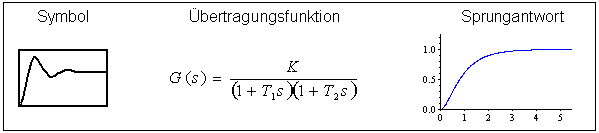
- Beispiele
- Zwei hintereinander geschaltete PT1-Glieder, Gleichstrommotor (Spannung → Drehzahl) mit berücksichtigter Induktivität
Der Regler
Der Regler hat die Aufgabe, die Regelgröße zu messen, sie mit dem Sollwert zu vergleichen und bei Abweichungen die Stellgröße so zu verändern, dass Soll- und Istwert der Regelgröße wieder übereinstimmen bzw. die Differenz minimal wird.
Die Wahl eines bestimmten Reglertyps richtet sich nach dem geforderten Zeitverhalten und der geforderten Regelgenauigkeit der Regelstrecke. Nachfolgend finden Sie eine Zusammenfassung der wichtigsten klassischen Reglertypen:
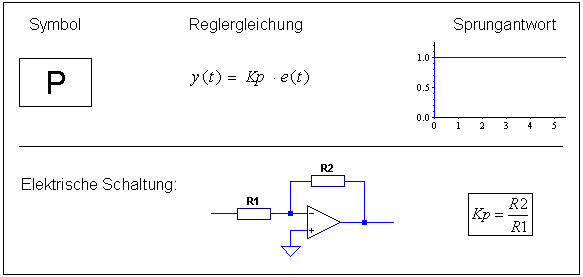
P-Regler
Der proportionalwirkende Regler multipliziert die Regelabweichung mit seinem Verstärkungsfaktor Kp und gibt das Ergebnis unverzögert weiter. Er unterscheidet sich prinzipiell nicht vom dynamischen Element P-Glied, ist nur eben künstlich hergestellt für den Einsatz als Regler. Der P-geregelte Kreis ist einfach und mittelschnell im Vergleich zu anderen Regelungen. Das Problem ist die bleibende Regelabweichung!
Software P-Regler:
y = Kp * e
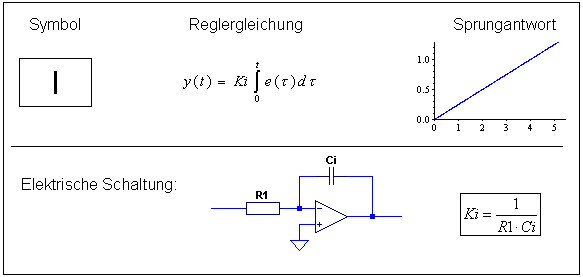
I-Regler
Der integralwirkende Regler summiert die Regelabweichung über der Zeit auf und multipliziert die Summe (d.h. das Integral) mit dem Faktor Ki. Je länger eine Regelabweichung ansteht, desto größer wird die Stellgröße des I-Reglers. Er unterscheidet sich prinzipiell nicht vom dynamischen Element I-Glied, ist nur eben künstlich hergestellt für den Einsatz als Regler. Der I-geregelte Kreis ist langsam im Vergleich zu anderen Regelungen. Er hat aber den Vorteil, dass die Abweichung vollständig eliminiert wird.
Software I-Regler:
esum = esum + e y = Ki * Ta * esum
esum ist die Summe aller bisherigen Abweichungen e. Der Parameter des Software I-Reglers ist abhängig von der Rechenschrittweite Ta (Abtastzeit). Je öfter gerechnet wird, desto öfter wird auch hinzugezählt (aufintegriert). Eine kleine Abtastzeit erfordert also einen kleineren Faktor, dies wird durch die Multiplikation mit Ta verwirklicht.
PI-Regler
Der PI-Regler ist die Kombination aus P- und I-Regler und kombiniert den Vorteil des P-Reglers, nämlich schnelle Reaktion, mit dem Vorteil des I-Reglers, der exakten Ausregelung. Der PI-geregelte Kreis ist also genau und mittelschnell.
Software PI-Regler:
esum = esum + e y = Kp * e + Ki * Ta * esum
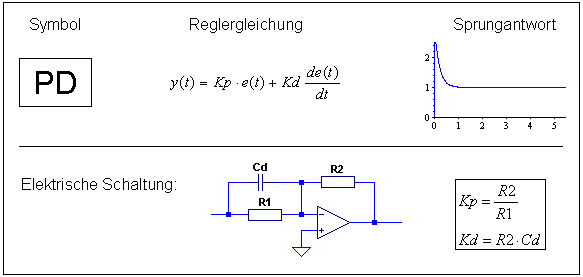
PD-Regler
Der proportional-differential wirkende Regler kombiniert den P-Regler mit einem D-Anteil. Der D-Anteil bewertet die Änderung einer Regelabweichung (er differenziert) und berechnet so deren Änderungsgeschwindigkeit. Diese wird mit dem Faktor Kd multipliziert und zum P-Anteil hinzuaddiert. Der PD-Regler reagiert damit schon auf Ankündigungen von Veränderungen, das bewirkt sozusagen ein Vorhalten beim Regeln.
Der PD-geregelte Kreis ist sehr schnell im Vergleich zu anderen Regelungen, und manche Regelkreise (solche mit zweifacher Integration) sind ohne D-Anteil überhaupt nicht stabilisierbar. Das Problem der proportionalen Regler, die bleibende Regelabweichung, ist beim PD-Regler allerdings weiterhin vorhanden!
Ein Nachteil aller Regler mit D-Anteil kann die Unruhe im Kreis sein. Ist das Sensorsignal verrauscht, so wird dieses Rauschen durch die Differenziation weiter verstärkt und wieder in den Kreis hineingegeben. Dadurch wird der Aktuator stärker belastet. Macht der Regler insbesondere sehr hohe Ausschläge als Folge von schnellen Änderungen des Sollwertes, dann kann es sein, dass das Stellglied oder der Aktuator diese nicht umsetzen kann - die Wirkung des D-Anteils würde dann durch die Begrenzung verpuffen, und das Einschwingverhalten wäre nicht wie berechnet, sondern meist langsamer. Dies gilt aber nur für große Sprünge. Bei den normalen kleinen Regelvorgängen zum Ausgleich von Störeinflüssen wirkt der D-Anteil wie beabsichtigt.
Software PD-Regler:
y = Kp * e + Kd * (e – ealt)/Ta ealt = e
Mit der neuesten Regelabweichung e und der vorhergehenden ealt wird der D-Anteil berechnet. Die Differenziation erfolgt damit angenähert durch Bildung des Differenzquotienten (e - ealt)/Ta.
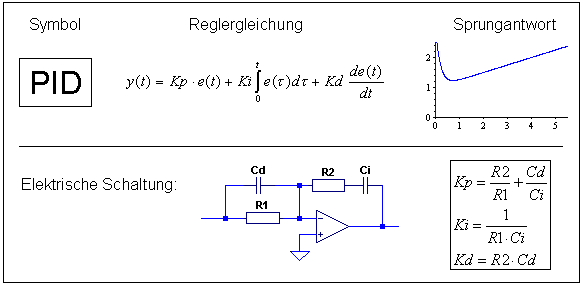
PID-Regler
Der PID Regler ist der universellste der klassischen Regler und vereinigt die guten Eigenschaften der anderen Regler. Zur Beschreibung der Eigenschaften des P-, I- und D-Anteils siehe die anderen Reglertypen. Der PID-geregelte Kreis ist genau und sehr schnell. In den meisten Anwendungen kommt deshalb der PID-Regler zum Einsatz.
Software PID-Regler:
esum = esum + e y = Kp * e + Ki * Ta * esum + Kd * (e – ealt)/Ta ealt = e
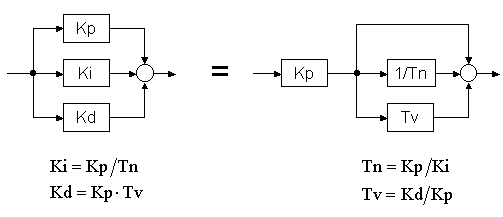
Alternative PID-Reglerstruktur:
Es gibt 2 Darstellungsmöglichkeiten, die inhaltlich identisch sind. In der analogen Regeltechnik ist noch die Darstellung mit der Nachstellzeit Tn und der Vorhaltezeit Tv üblich. Die Umrechnung zwischen den beiden Strukturen ist mit den angegebenen Formeln möglich.
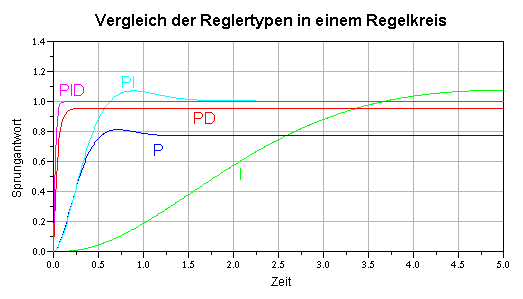
Vergleich der Reglertypen
In der folgenden Abbildung ist der Vergleich von P-, I-, PI-, PD- und PID-Regler in einem Regelkreis mit PT2-Glied als Regelstrecke dargestellt. Es ist deutlich zu sehen, dass die Regler ohne I-Anteil (P und PD) eine bleibende Regelabweichung aufweisen. Erst die Regler mit I-Anteil können auf den Endwert von 1 ausregeln. Beim reinen I-Regler geht das so langsam, dass es gar nicht mehr auf dem Diagramm zu sehen ist. Der Hauptzweck eines I-Anteils ist also die Vermeidung bleibender Regelabweichungen. Daher ist ein I-Anteil normalerweise nicht nötig, wenn die Strecke schon einen I-Anteil besitzt. Ausnahme: Es wird ein doppelter I-Anteil zur Vermeidung von Schleppfehlern benötigt.
Die schnellsten Regler sind die mit einem D-Anteil (PD und PID). Der D-Anteil kommt deshalb hauptsächlich zum Einsatz, wenn schnelle Dynamik gefragt ist oder die Strecke selbst schon instabil ist. Voraussetzung für die Schnelligkeit ist allerdings, dass keine Begrenzung im Stellglied oder Aktuator auftritt. In der Praxis ist eine Begrenzung meistens nicht zu vermeiden, deshalb gilt die Sprungantwort in der Praxis nur für kleine Sprünge.
Die Regler ohne D-Anteil, aber mit P-Anteil (P und PI) sind mittelschnell. Für einfache Regelaufgaben reicht auch oft schon ein reiner P-Regler aus, wenn die bleibende Regelabweichung vernachlässigt werden kann oder weil die Strecke schon einen I-Anteil besitzt.
Aus diesem Vergleich wird klar, warum der PID-Regler so beliebt ist, er vereinigt die Vorzüge aller anderen Regler.
Digitaler Regler
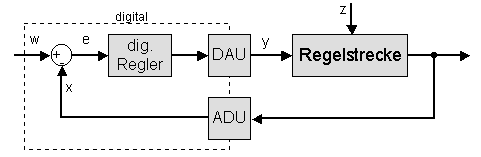
Durch die Einführung leistungsfähiger und preiswerter Mikroprozessoren hat sich der digitale Regler mehr und mehr durchgesetzt. Im Gegensatz zum analogen Regler werden die Signale nicht mehr analog mit Operationsverstärker verarbeitet, sondern mit einem Mikroprozessor errechnet. Bevor das Signal vom Mikroprozessor bearbeitet werden kann, muss zunächst das Eingangssignal (Istwert) mit einem Analog-Digital-Umsetzer (ADU) digitalisiert werden, d.h. in einen Zahlenwert umgewandelt werden. Das vom digitalen Regler errechnete Ausgangssignal (Stellgröße) wird wiederum zur Ansteuerung des Stellglieds mit einem Digital-Analog-Umsetzer (DAU) in ein analoges Signal gewandelt. Funktionell unterscheiden sich analoger und digitaler Regler jedoch nicht wesentlich, es müssen nur die Schnittstellen angepasst werden.
Da die Wandlungen und das Regelprogramm eine gewisse Zeit beanspruchen, vergeht pro Durchlauf die sogenannte Takt- oder Abtastzeit. Diese Zeit wirkt sich im Regelkreis wie ein Totzeitglied mit der halben Abtastzeit als Totzeit aus. Das verursacht eine zusätzliche Phasenverschiebung, was sich ungünstig auf die Stabilität des Regelkreises auswirken kann. Ist die Abtastzeit sehr viel kleiner als die dominierende Zeitkonstante der Strecke, dann spricht man von quasi-kontinuierlichem Verhalten, da sich der digitale Regler ähnlich wie ein analoger Regler verhält. Der digitale Regler kann dann wie ein analoger dimensioniert werden. Ist die Abtastzeit größer, kann sie nicht mehr vernachlässigt werden, dann muss sie auch beim Reglerentwurf berücksichtigt werden.
Vorteile digitaler Regler:
- Die Verarbeitung erfolgt driftfrei.
- Es lassen sich nichtlineare Kennlinien, intelligentes Verhalten oder adaptive Regelung leichter realisieren.
- Der Regler kann bei Bedarf per Software neu konfiguriert und parametriert werden
Digitale Realisierung am Beispiel des PID-Algorithmus
Ausgehend von der Differentialgleichung für kontinuierliche Systeme wird die Differenzengleichung für zeitdiskrete Systeme erstellt. Daraus folgt dann der Stellungsalgorithmus in allgemeiner Form.
Ta = Abtastzeit; k = Nummer der Abtastung
Kp = Proportionalbeiwert; Ki = Integrierbeiwert; Kd = Differenzierbeiwert
Differentialgleichung für den kontinuierlichen PID-Regler:
- [math] y(t) \;=\; Kp \!\cdot\! e(t) + Ki \int_0^t e(\tau) \, d\tau + Kd \, \frac{de(t)}{dt} [/math]
Differenzengleichung für den zeitdiskreten PID-Regler:
- [math] y_k \;=\; Kp \!\cdot\! e_k + Ki \!\cdot\! Ta \sum_{i=0}^k e_i + \frac{Kd}{Ta}\, ( e_k - e_{k-1} ) [/math]
PID Stellungs-Algorithmus:
- [math] y_k \;=\; y_{k-1} + q_0 \!\cdot\! e_k + q_1 \!\cdot\! e_{k-1} + q_2 \!\cdot\! e_{k-2} [/math]
Mit den Parametern:
- [math] q_0 \,=\, Kp + Ki \!\cdot\! Ta + \frac{Kd}{Ta} \, , \quad q_1 \,=\, -Kp - 2 \, \frac{Kd}{Ta} \, , \quad q_2 \,=\, \frac{Kd}{Ta} [/math]
Umsetzung in Code nach der Differenzengleichung:
Im Code wurden einige Variablen umbenannt, da die Indexschreibweise nicht möglich ist.
y entspricht yk, e entspricht ek, ealt entspricht ek-1, esum ist die Summenbildung
In der Praxis wird man die Ausdrücke Ki*Ta und Kd/Ta vorab berechnen und mit Ersatzvariablen in die Reglergleichung einsetzen. Der Verständlichkeit halber wurde es hier im Code belassen. Des weiteren kann eine Begrenzung von esum notwendig werden, um einen Variablenüberlauf oder Windup-Effekt zu vermeiden.
Der nachfolgende Code wird im Rhythmus der Abtastzeit Ta immer wieder aufgerufen.
e = w - x; //Vergleich esum = esum + e; //Integration I-Anteil y = Kp*e + Ki*Ta*esum + Kd/Ta*(e – ealt); //Reglergleichung ealt = e;
Alternative Umsetzung in Code nach dem Stellungsalgorithmus:
y entspricht yk, yalt entspricht yk-1, e entspricht ek, ealt entspricht ek-1, ealt2 entspricht ek-2
e = w - x; //Vergleich y = yalt + q0*e + q1*ealt + q2*ealt2; //Reglergleichung ealt2 = ealt; ealt = e; yalt = y;
Dimensionierung des Reglers
Die Auswahl des Reglertyps ist heutzutage bei den digitalen Reglern nicht mehr so kritisch, da der Mehraufwand in Software für einen PID-Regler gegenüber einfacheren Typen kaum zu Buche schlägt. Im Prinzip ist man deshalb mit einem PID-Regler fast immer auf der richtigen Seite, mit einer Ausnahme, bei einer Strecke mit reiner Totzeit. Die folgende Tabelle gibt eine Hilfestellung zur Auswahl des Reglers.
Geeignete Reglertypen für die unterschiedlichen Regelstrecken Strecke Regler P PD PI PID reine Totzeit geeignet1.Ordnung mit kleiner Totzeit gut geeignet gut geeignet 2.Ordnung mit kleiner Totzeit gut geeignet höhere Ordnung gut geeignet I-Glied und Verzögerung geeignet gut geeignet geeignetgut geeignet
Nachdem man einen geeigneten Reglertyp ausgewählt hat, stellt sich noch die Frage, wie man die Reglerparameter Kp, Ki, und Kd optimiert. Im Laufe der Zeit wurden viele Methoden zur Dimensionierung der Reglerparameter entwickelt, aber es können hier nicht alle aufgelistet werden. Diese Aufzählung beschränkt sich auf die einfacheren und gängigen Methoden der Parametrierung.
Dimensionierung durch Probieren (Empirisches Einstellen)
Methode 1
Diese Methode ist geeignet um einfache Systeme zu dimensionieren, insbesondere wenn man bereits Erfahrung mit ähnlichen Regelkreisen hat. Man fängt mit einer unkritischen Einstellung (Kp klein, Ki = 0, Kd = 0) an und erhöht langsam die Verstärkung Kp, bis die Dämpfung schlecht wird. Falls eine Schwingneigung auftritt, muss die Verstärkung wieder etwas zurück genommen werden. Dann nimmt man allmählich den Integralanteil hinzu, erhöht ihn in Schritten und probiert solange herum, bis das Ergebnis einigermaßen passt. Bei Bedarf kann noch ein D-Anteil (PID-Struktur) probiert werden. Wenn dabei die Regelung stabiler wird, kann noch mal Kp und Ki erhöht werden, bis man endgültig zufrieden ist.
Methode 2
Alle Anteile erstmal auf 0. Dann erhöht man Kp so lange bis das System deutlich schwingt. Danach wird der Kd so lange erhöht bis das System nicht mehr schwingt. Anschliessend kann noch ein kleiner Ki Anteil hinzugegeben werden.
Es dürfte klar sein, dass so eine Optimierung im Blindflug nicht immer das Optimum ergibt, aber es ist eine gängige praktische Methode zur Ermittlung der Reglerparameter. Besser sieht es aus, wenn in einer Simulation empirisch optimiert wird. Zusätzliche Informationen über die Stabilität erlauben hierbei eine gezieltere Optimierung. Zudem ist das Probieren im Simulator gefahrlos möglich, was in der Realität nicht immer der Fall ist. Geeignete Programme zur Simulation sind hier vorgestellt. Allerdings muss für eine Simulation die Regelstrecke bekannt sein. Ist das nicht der Fall, so bleibt nur das einfache Probieren oder das Einstellen nach der Schwingungsmethode wie im folgenden beschrieben.
Dimensionierung nach Einstellregeln
Die Dimensionierung nach Rezept ist eine praktische Methode ohne viel Rechnerei und Hilfsmittel, eine Methode also für den Praktiker. Die bekanntesten Einstellregeln sind von Ziegler/Nichols und von Chien/Hrones/Reswick. Darüber hinaus gibt es noch eine Vielzahl anderer Einstelltabellen, auf die hier aber verzichtet wird, das würde den Rahmen dieses Artikels sprengen. An der Vielzahl kann man schon ersehen, dass es kein universell gültiges Rezept gibt und mit diesen Tabellen nicht unbedingt das Optimum erreicht wird, eine Nachoptimierung kann nötig sein.
Bei Ziegler/Nichols unterscheidet man noch zwischen der Schwingungsmethode und der Einstellung nach der Sprungantwort.
Einstellung nach der Schwingungsmethode:
Bei der Schwingungsmethode nach Ziegler/Nichols werden die Reglerparameter so verstellt, dass die Stabilitätsgrenze erreicht wird und der Regelkreis zu schwingen beginnt, d.h. die Regelgröße periodische Schwingungen ausführt. Aus der so gefundenen Einstellung können die Reglerparameter ermittelt werden. Dieses Verfahren ist nur auf Regelstrecken anwendbar, bei denen ein Schwingen keinen Schaden anrichtet und die überhaupt instabil gemacht werden können. Die Vorgehensweise ist folgende:
- Einstellung des Reglers als reinen P-Regler: Ki = 0 und Kd = 0
- Die Reglerverstärkung Kp wird solange vergrößert, bis sich der geschlossene Regelkreis an der Stabilitätsgrenze befindet und Dauerschwingungen ausführt.
- Der dabei eingestellte Wert Kp wird als Kpkrit bezeichnet.
- Die Periodendauer der sich einstellenden Dauerschwingung Tkrit wird gemessen.
- Anhand der folgenden Tabelle werden dann die Reglerparameter bestimmt.
|
|
Der Vorteil dieses Verfahrens liegt darin, dass die Untersuchung während des Betriebes und ohne Öffnen des Regelkreises durchgeführt werden kann. Der Nachteil an dem Verfahren ist, dass es nur auf Strecken angewendet werden kann, die auch zum Schwingen gebracht werden können.
Einstellung nach der Sprungantwort:
Diese Methode der Parameterbestimmung beruht auf der Aufnahme der Sprungantwort der Regelstrecke. Es eignet sich auch für Strecken, die nicht zum Schwingen gebracht werden können. Der Regelkreis muss allerdings geöffnet werden.
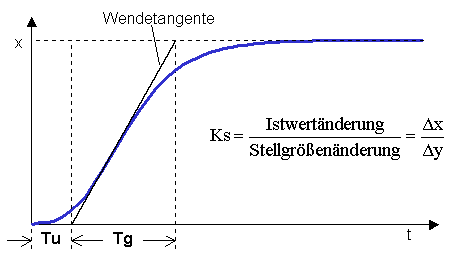
Vorgehensweise: Es wird die Sprungantwort aufgenommen und durch Einzeichnen der Wendetangente die Verzugszeit Tu und die Ausgleichszeit Tg ermittelt.
Mit den so festgestellten Werten werden die Parameter für den einzusetzenden Regler gemäß nachstehenden Tabellen ermittelt.
|
|
|
|
Dimensionierung mit dem Bodediagramm
Ein Bode-Diagramm ist die grafische Darstellung des Frequenzganges. Es werden der Betrag der Übertragungsfunktion (Amplitudengang) und der Verlauf des Phasenwinkels (Phasengang) als Funktion der Frequenz aufgetragen. Die Frequenzachse und die Amplitudenachse werden logarithmisch dargestellt. Die logarithmische Darstellung hat den Vorteil, dass eine Multiplikation auf eine einfache Addition zurückgeführt wird. Somit wird eine Hintereinanderschaltung von Systemen im Blockschaltbild zu einer einfachen Addition im Bodediagramm.
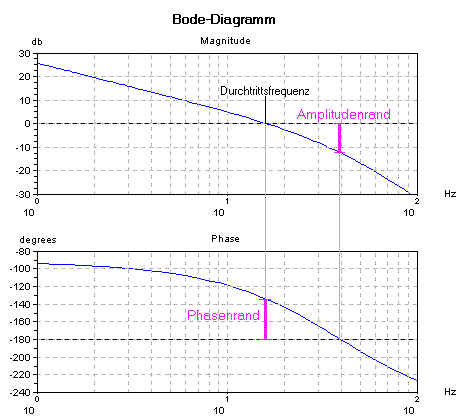
Das Zeitverhalten des rückgekoppelten Regelkreises hängt entscheidend vom Verlauf des Frequenzganges der offenen Regelschleife in der Umgebung des Durchtretens durch die 0dB-Achse ab. In der Regelungstechnik wird daher der offene Regelkreis im Bode-Diagramm aufgetragen. Das erlaubt einen schnellen Überblick über Stabilität und möglichen Reserven zur Optimierung. Ein Kriterium für die Stabilität der Schleife ist der Phasenrand und der Amplitudenrand. Der Phasenrand ist der Abstand (Phasenreserve) zur -180°-Linie bei der Durchtrittsfrequenz. Die Durchtrittsfrequenz ist diejenige Frequenz, bei der der Amplitudengang durch die 0dB-Linie geht. Siehe auch folgendes Bode-Diagramm.
| Regel: Eine geschlossene Regelschleife arbeitet genau dann stabil, wenn der Phasenrand positiv ist. |
Wird diese Bedingung verletzt, so wird in diesem Frequenzbereich die im Rückführzweig der Regelung eingebrachte Gegenkopplung zu einer Mitkopplung und das System kann schwingen.
Beim Reglerentwurf sind folgende Punkte zu beachten:
- Der Phasenrand muss positiv sein. Der geschlossene Regelkreis kann sonst instabil sein.
- Je größer der Phasenrand ist, desto größer ist die Stabilitätsreserve des Regelkreises und desto höher ist die Dämpfung des Regelkreises. Üblich sind Werte von 40°...70° für gutes Führungsverhalten und 20°...50° für gutes Störverhalten.
- Die Durchtrittsfrequenz ist ein Maß für die Schnelligkeit des Regelkreises, je höher, desto schneller ist die Reaktion auf Änderungen der Führungsgröße oder Störungen.
Hier ein Beispiel zur Dimensionierung mit dem Bode-Diagramm.
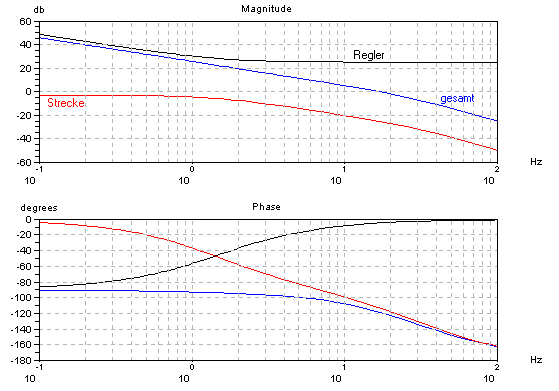
Die Strecke ist rot dargestellt und besteht in dem Beispiel aus einem nicht schwingfähigem PT2-Glied. Man sucht sich den Punkt, wo die Strecke für sich alleine noch ausreichend Phasenreserve hat, z.B. 70°. In dem Beispiel also die Frequenz, bei der die Strecke –110° Phasendrehung aufweist. Das ist etwa bei 15Hz. Da hat die Strecke ungefähr eine Dämpfung von 25dB. Wenn man nun diese Dämpfung durch eine Verstärkung von 25dB kompensiert, dann wird dieser Punkt zur Durchtrittsfrequenz. D.h. man wählt den P-Anteil des Reglers Kp=18, denn 25dB entspricht ungefähr dem Faktor 18. Um die Regelabweichung zu minimieren, wird noch ein I-Anteil hinzugefügt.
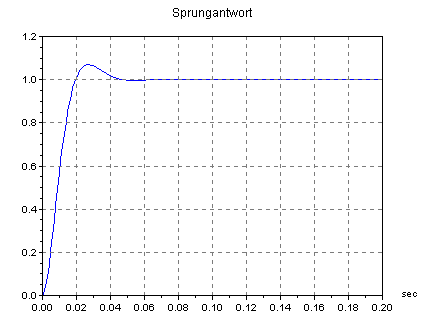
Üblicherweise wählt man für die Grenzfrequenz des PI-Reglers die Grenzfrequenz des dominierenden Streckenteils, in dem Beispiel ca. 1.4Hz. Damit ergibt sich ein I-Anteil von 170. Im Bode-Diagramm ist der PI-Regler als schwarze Kurve eingezeichnet. Die Addition der Strecke und des Reglers im Bode-Diagramm führt dann zum Frequenzgang des offenen Regelkreises (blaue Kurve). Die resultierende Durchtrittsfrequenz ist wie gewählt bei etwa 15Hz. Der Phasenrand hat sich durch den I-Anteil im Regler auf ca. 60° reduziert, ist aber noch ausreichend. Das Einschwingen des geschlossenen Regelkreises für diese Dimensionierung sieht dann folgendermaßen aus:
Bei Bedarf könnte noch ein D-Anteil (PID-Regler) hinzugenommen werden, das würde die Phase anheben und man könnte dadurch die Durchtrittsfrequenz weiter nach oben schieben. In der Praxis wird dies allerdings wegen der wahrscheinlichen Begrenzung des Stellglieds kein schnelleres Einschwingen mehr bringen.
Begrenzungen oder Nichtlinearitäten werden bei der Dimensionierung mit dem Bode-Diagramm nicht berücksichtigt. Das ist ein Nachteil dieser Methode. Eventuell muss deshalb noch einmal im Zeitbereich nachoptimiert werden.
Dimensionierung mit der Ortskurve
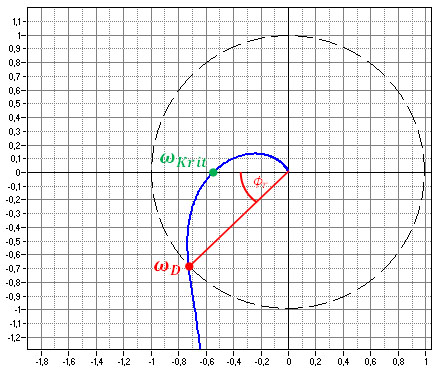
Eine Alternative zur Dimensionierung mit dem Bodediagramm stellt die Methode über die Ortskurve des offenen Regelkreises dar. Bei diesem Verfahren ist schnell auf einem Blick ersichtlich ob der Regelkreis stabil ist.
Liegt der Punkt –1 auf der Realteilachse links von der Ortskurve in Richtung steigendem ω (omega) so ist der Regelkreis stabil. Der Abstand zu der kritischen Kreisfrequenz ωKrit von der Imaginärteilachse ist die Verstärkung Vr. Mit diesem Wert lässt sich der Amplitudenrand nach folgender Formelermitteln: Ar = 20 lg (1/Vr) in dB
Die Durchtrittskreisfrequenz ωD liegt an dem Punkt, wo der Betrag aus Realteil und Imaginärteil 1 ergibt. Wenn man weiß, wo die Durchtrittskreisfrequenz ist, dann kann man den Phasenrand bestimmen. Dies ist der Winkel zwischen der –180°-Linie zu ωD.
Hilfsprogramme zur Analyse und Optimierung
Die Analyse und Optimierung von Regelkreisen wird wesentlich erleichtert durch die Zuhilfenahme von Programmen. Es erspart einem eine komplizierte Rechnerei von Hand oder umfangreiche Testläufe. Stellvertretend für all die verfügbaren Programme werden hier zwei Freeware-Programme vorgestellt, die dafür gut geeignet sind. Die Beschreibung hier ersetzt aber keine Tutorials, es wird nur die Anwendung für die Regelungstechnik beschrieben.
Scilab/Scicos
Scilab ist ein wissenschaftlich-technisches Softwarepaket für numerische Berechnungen. Scicos ist eine Erweiterung dazu, die eine blockorientierte und modellbasierte Simulation und Analyse von dynamischen Systemen bietet. Dieses Softwarepaket kann von der Scilab Homepage herunter geladen werden.
Scilab
Mit Scilab ist es sehr einfach ein Bode-Diagramm zu zeichnen, es bedarf nur 3 Zeilen Code.
s=poly(0,'s');
G=syslin('c',0.72/(0.11*s+1));
bode(G)
Die 1.Zeile s=poly(0,'s'); legt die Variable s als Polynomvariable fest. Dies braucht in einer Sitzung nur einmal gemacht zu werden. Die 2.Zeile G=syslin('c',0.72/(0.11*s+1)); definiert ein lineares System mit der Übertragungsfunktion 0.72/(0.11s+1). Die 3.Zeile bode(G) zeichnet das Bode-Diagramm des zuvor mit syslin definierten Systems G. Zu beachten ist, dass Scilab auf der x-Achse im Bode-Diagramm die Frequenz in Hertz und nicht wie üblich die Kreisfrequenz darstellt. Anstelle des Bode-Diagramms kann auch die Sprungantwort gezeichnet werden. Dies geschieht mit folgenden Befehlen:
xbasc();
t=[0:0.001:2];
y=csim('step',t,G);
plot2d(t,y)
xbasc() löscht den letzten Plot mit dem Bode-Diagramm und mit t=[0:0.001:2] wird ein Vektor t mit den angegebenen Zeiten im Intervall von 1ms definiert. Die Zeile y=csim('step',t,G) berechnet die Sprungantwort des zuvor mit syslin definierten Systems G und speichert sie in y ab. Das Ergebnis wird dann mit plot2d(t,y) dargestellt. Bei Bedarf können noch Gitternetzlinien mit dem Befehl xgrid() hinzugefügt werden.
Ergänzend hier noch ein Scilab-Skript, welches recht hilfreich bei der Dimensionierung mit dem Bode-Diagramm ist. Den nachfolgenden Code einfach in das SciPad-Fenster (Editor von Scilab) kopieren und starten. Es werden 2 Grafikfenster angezeigt, eines mit dem Bode-Diagramm und ein zweites mit der Sprungantwort. Man kann im Skript die Streckencharakteristik anpassen und verschiedene Reglerparameter ausprobieren.
Ks=0.72; // Verstärkung der Strecke
T1=0.11; // Zeitkonstante 1
T2=0.005; // Zeitkonstante 2
Kp=18; // Proportionalbeiwert
Ki=170; // Integralbeiwert
Kd=0; // Differenzialbeiwert
s=poly(0,'s'); // definiert s als Polynomvariable
P=(T1*s+1)*(T2*s+1); // Streckencharakteristik
Gs=syslin('c',Ks,P) // Übertragungsfunktion der Strecke
RZ=poly([Ki Kp Kd],'s','coeff') // Zählerpolynom des Reglers
RN=poly([0 1],'s','coeff') // Nennerpolynom des Reglers
Gr=syslin('c',RZ,RN) // Übertragungsfunktion des Reglers
G=Gr*Gs // Übertragungsfunktion gesamt
xset("window",0);
xbasc(0);
bode([Gr;G;Gs],0.1,100,['Regler';'gesamt';'Strecke'])
Gcl=G/(G+1) // geschlossene Regelschleife
t=0:0.001:0.2;
y=csim('step',t,Gcl); // berechnet Sprungantwort
xset("window",1);
xbasc(1);
plot2d(t,y,2);
xgrid();
xtitle("Sprungantwort","sec");
Scicos
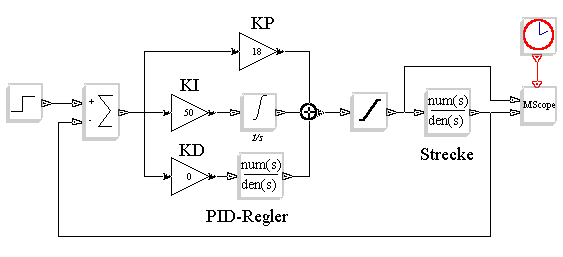
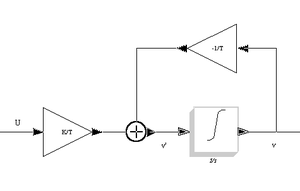
Eine weitere Möglichkeit zur Simulation im Zeitbereich bietet Scicos. Die Modellierung geschieht mit einem grafischen Editor, in dem Blöcke mit vordefinierten oder selbstgemachten Funktionen miteinander verbunden werden. Ein einfaches Modell eines Regelkreises mit PID-Regler sieht folgendermaßen aus:
Der PID-Regler ist mit seinen 3 Zweigen (P, I und D) dargestellt. In den Verstärkerblöcken kann durch Ändern der Reglerparameter (KP, KI und KD) der Regler optimiert werden. Die Strecke ist in diesem Beispiel nur ein einzelner Block, in dem die Übertragungsfunktion eingegeben wird. Man kann die Strecke auch detaillierter mit einzelnen Funktionsblöcken darstellen. Ein Beispiel eines komplexen Blockschaltbilds für einen balancierenden Bot ist unter diesem Link zu finden.
Der Vorteil der Simulation mit Scicos ist die Möglichkeit Nichtlinearitäten zu berücksichtigen und die Kombination von kontinuierlichen und diskreten Funktionen. Das heißt, man kann einen digitalen Regler mit seinen diskreten Schritten und eine analoge Strecke, als kontinuierliche Funktion eingegeben, zusammen simulieren. Scicos bietet sogar einen 'Scifunc'-Block, mit dem Rechenschritte des digitalen Reglers nachgebildet werden können. Damit wird sowohl das dynamische Verhalten, verursacht durch die Abtastzeit Ta, als auch die etwas unterschiedliche Dynamik durch die digitale Ausführung eines I- und D-Anteils richtig simuliert. Ein Beispiel für den Einsatz des Scifunc-Blocks ist in folgendem Blockschaltbild zu sehen.
Beispiel: Drehzahlregelung mit digitalem Regler
Die globalen Variablen für die Reglerparameter und die Abtastzeit werden unter dem Menüpunkt „Edit - Context“ abgelegt.
Kp=18; Ki=60; Ta=0.01;
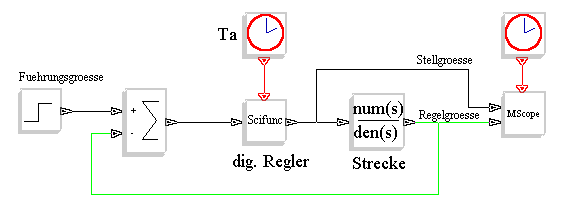
In den Taktgeber für den digitalen Regler wird als Clock-Periode die Abtastzeit Ta eingetragen. In das Dialogfenster zum Scifunc-Block wird folgender Code zur Simulation des digitalen PI-Reglers eingetragen:
z=z+Ki*Ta*u1 if z>5 then z=5; end y1=Kp*u1+z if y1>5 then y1=5; end
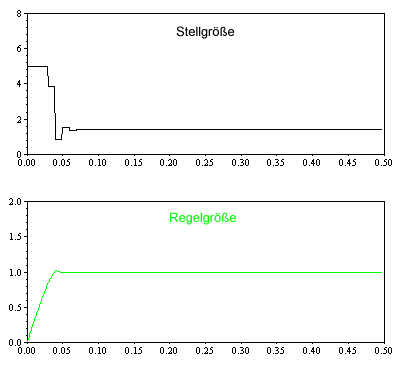
z entspricht der Variable esum vom Beispiel des digitalen Drehzahlreglers; u1 ist die Eingangsvariable und y1 die Ausgangsvariable des Scifunc-Blocks. In den Block für die Strecke wird die Übertragungsfunktion eingetragen. Als Zähler die Verstärkung Ks, also 0.72. Im Nenner das Polynom (1+0.11*s) für die Charakteristik der Strecke. Mit ‚Simulate – Run’ wird die Simulation gestartet. Als Ergebnis sollte das Einschwingen der Stellgröße (schwarz) und der Regelgröße (grün), wie in folgender Abbildung erscheinen.
Man kann nun mit den Reglerparametern und verschiedenen Abtastzeiten spielen, um zu sehen wie sich die Änderungen auswirken. Zum Beispiel wird bei einer Verdopplung der Abtastzeit der Regelkreis bereits instabil.
Diese Beispiele sind nur ein kurzer Auszug von den Möglichkeiten mit Scilab/Scicos für den Einsatz in der Regelungstechnik. Darüber hinaus ist es auch sehr gut geeignet bei anderen Optimierungsverfahren wie z.B. beim WOK-Verfahren (Wurzelortskurven) oder zur Analyse und Optimierung von modernen Reglern wie z.B. Zustandsregler und Kalmanfilter.
LTspice/SwitcherCad III
Dieses Programm ist ein SPICE-Derivat von der Firma Linear Technology und ist unter den 2 Namen LTspice und SwitcherCad III bekannt. Der Einfachheit halber wird für die weitere Beschreibung hier nur der Name LTspice verwendet. Das Programm ist Freeware und kann unter diesem Link herunter geladen werden. http://ltspice.linear.com/software/LTspiceIV.exe
LTspice ist ein Simulationsprogramm zur Analyse von elektronischen Schaltungen. Mit LTspice kann sowohl im Zeitbereich als auch im Frequenzbereich analysiert werden und bietet sich dadurch mit den entsprechenden Modellen auch für den Einsatz in der Regelungstechnik an. Wer sich bereits mit SPICE-Programmen auskennt, für den sollte es auch in der Regelungstechnik die 1.Wahl sein.
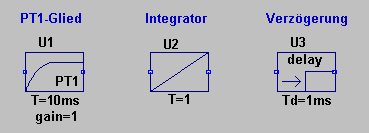
Der Vorteil von LTspice ist die Möglichkeit einer sehr detaillierten Analyse, vorausgesetzt die Modelle sind auch so detailliert nachgebildet. Insbesondere für analoge Regler, wo die elektrische Schaltung direkt umgesetzt werden kann, empfiehlt sich der Einsatz von LTspice. Der Nachteil ist, LTspice ist nicht auf regeltechnische Belange ausgelegt worden und spezifische Symbole für die Regelungstechnik müssen selbst erstellt werden. Einige selbst erstellte Symbole für dynamische Grundelemente in LTspice sind hier abgebildet.
Die 3 Symbole können hier heruntergeladen werden. Weitere Symbole können anhand dieser Beispiele sehr leicht selbst erstellt werden. Ein P-Glied kann durch eine spannungsgesteuerte Spannungsquelle (E-Source) oder Operationsverstärker mit einstellbarer Verstärkung dargestellt werden.
Analyse im Zeitbereich
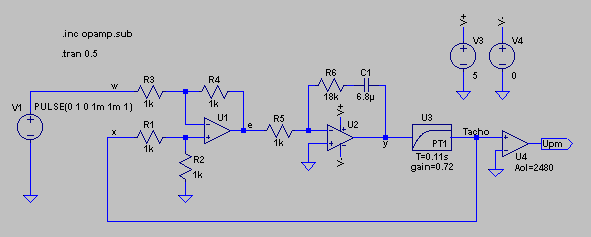
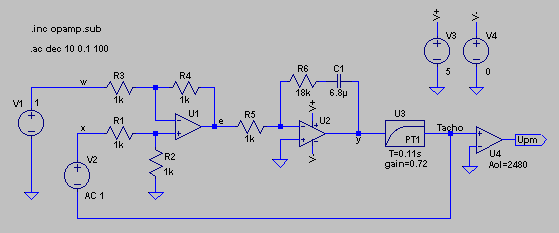
Das Beispiel des Drehzahlreglers mit analogem Regler wird hier mit LTspice simuliert. Das Schaltbild des Regelkreises zeigt nachfolgende Abbildung.
Der Vergleicher (U1) und der analoge PI-Regler (U2) sind so dargestellt, wie es auch in Wirklichkeit ausgeführt werden kann. Da der PI-Regler in der Schaltung bereits invertiert, wurden die Eingänge am Vergleicher vertauscht, damit die Polarität wieder stimmt. Der Rest des Regelkreises wurde stark vereinfacht, kann aber nach Bedarf auch ausführlicher dargestellt werden. Das PT1-Glied U3 simuliert die Strecke des Regelkreises und der Verstärker U4 dient nur zur Umrechnung auf die Drehzahl. Zur Simulation im Zeitbereich wird auf den Führungswert w mit der Spannungsquelle V1 ein Sprung gegeben. In der Reglerschaltung wurde bewusst ein Operationsverstärker mit Versorgungsspannung gewählt, damit auch der Einfluss einer Begrenzung mit simuliert wird. Die Zeitbereichsanalyse wird durch den LTspicebefehl .TRAN erreicht. Die Sprungantwort (Tachospannung) bei diesem Regelkreis sieht dann folgendermaßen aus.
Durch Ändern der Bauelemente R5, R6 und C1 kann man den Regler optimieren. Eine Umrechnung auf die Reglerparameter Kp und Ki ist mit folgenden Formeln möglich, siehe auch PI-Regler:
Kp = R6/R5
Ki = 1/(R5*C1)
Mit einem Mausklick auf den entsprechenden Knoten in der Schaltung können noch weitere Signale, wie z.B. die Stellgröße y angezeigt werden. Durch Verändern der Versorgungsspannung V3, V4 kann man sich auch die Auswirkung der Begrenzung ansehen.
Analyse im Frequenzbereich
Für die Darstellung des Bode-Diagramms der offenen Regelschleife in LTspice muss ein Trick angewendet werden, denn durch das Auftrennen der Regelschleife würde der Arbeitspunkt verloren gehen und dadurch die offene Schleife ohne Gegenkopplung an den Anschlag fahren.
Mit einer zusätzlichen Spannungsquelle in der Schleife kann man dieses Problem umgehen. Die Schleife bleibt für den Erhalt des Arbeitspunktes weiterhin geschlossen und man kann trotzdem die Verstärkung der offenen Schleife durch das Verhältnis der Spannung vor und hinter der Spannungsquelle bestimmen. Das erweiterte Blockschaltbild sieht folgendermaßen aus.
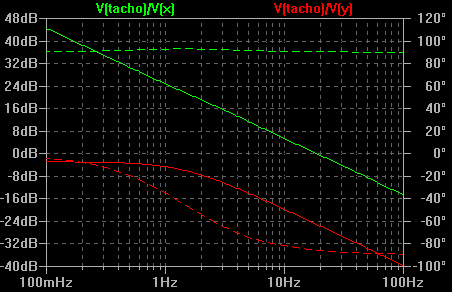
V2 ist die zusätzliche Spannungsquelle für die AC-Analyse. Die Spannungsquelle V1 wird von Pulsform auf Gleichspannung umgestellt. Sie wird so gewählt, dass sich der gewünschte Arbeitspunkt einstellt. Durch den LTspicebefehl .AC wird die Analyse im Frequenzbereich veranlasst. Um das Bode-Diagramm des offenen Regelkreises darzustellen, wird als Kurve nicht ein einzelner Knoten ausgewählt, sondern das Verhältnis der Spannung vom Ende zum Anfang des Regelkreises, in unserem Beispiel also V(tacho)/V(x). Zur Anzeige kommt dann das Bode-Diagramm (grüne Kurve) der offenen Schleife, wie in der folgenden Abbildung zu sehen. Für den Amplitudengang (durchgezogene Linien) gilt die linke Skala in dB, für den Phasengang (gestrichelte Linien) die rechte Skala in Grad.
Zusätzlich ist noch das Bode-Diagramm der Strecke (rote Kurve) zu sehen. Dies ist durch einfaches Hinzufügen einer weiteren Kurve mit dem Ausdruck V(tacho)/V(y) durchgeführt worden.
Im Gegensatz zur üblichen Darstellung des Bode-Diagramms eines offenen Regelkreises, beinhaltet das mit LTspice erstellte Bode-Diagramm auch die -180 Grad Phasendrehung der Gegenkopplung. Der Phasenrand ist deshalb nicht auf -180 Grad sondern auf 0 Grad zu beziehen. In unserem Beispiel ist der Phasenrand etwa 90 Grad, also ein sehr stabiler Regelkreis. Zu beachten ist, dass die Frequenzachse des Bode-Diagramms wie auch schon bei Scilab in der Einheit Hertz anstatt wie üblich in der Kreisfrequenzeinheit rad/s dargestellt ist.
Modellierung eines Motors/Antriebs
Der Motor ist ein oft verwendeter Aktuator in der Robotik. Deshalb wird hier am Beispiel des Gleichstrommotors mit Permanentmagnet (Nebenschlussmotor) die Modellbildung gezeigt. Zur Modellierung gibt es mehrere Möglichkeiten. Je nachdem wie detailliert die Simulation sein soll, kann man sich ein Modell, von sehr einfach bis sehr detailliert, auswählen. Zwei Zeitkonstanten bestimmen die Dynamik eines Gleichstrommotors. Eine davon ist die mechanische Zeitkonstante, die ist meistens die dominierende Zeitkonstante und wird durch das Trägheitsmoment J des Rotors verursacht. Die zweite Zeitkonstante ist die elektrische Zeitkonstante, sie wird durch die Induktivität L bestimmt. Bei einfachen Regelungen kann in den meisten Fällen die elektrische Zeitkonstante vernachlässigt werden, damit reduziert sich das Modell auf ein einzelnes PT1-Glied.
Definition: Motor und Antrieb
Als Motor wird hier der Motor alleine verstanden. Die Ausgangsgröße ist die Winkelgeschwindigkeit w (Drehzahl).
Als Antrieb wird hier der komplette Antrieb eines Fahrzeugs verstanden, also Motor inklusive Getriebe und Masse des Fahrzeugs. Für die Dynamik ist nicht nur das Trägheitsmoment des Motors sondern auch die Masse des Fahrzeugs verantwortlich. Die Ausgangsgröße der Einheit „Antrieb“ ist die Geschwindigkeit v.
Die hier vorgestellten Modelle gelten sowohl für einen Motor als auch für einen kompletten Antrieb, wenn man die Elastizität und das Spiel des Getriebes vernachlässigt.
Einfaches Modell mit PT1-Glied
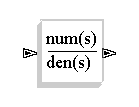
Die einfachste Art einen Motor oder Antrieb zu simulieren, ist mit einem PT1-Glied als Modell. Das Simulationsprogramm Scicos bietet dazu einen Block zur Eingabe der Übertragungsfunktion (num(s)=Zähler, den(s)=Nenner der Übertragungsfunktion).
| Übertragungsfunktion:
|
Beispiel:
num(s) = K = 0.72 den(s) = 1 + Ts = 1 + 0.11s |
|
Wird nicht nur das Ausgangssignal, also die Geschwindigkeit oder Drehzahl in der Simulation benötigt, sondern auch die Beschleunigung, dann kann nachfolgendes Modell verwendet werden. Dieses Modell ist der Differentialgleichung eines PT1-Glieds nachempfunden und liefert das gleiche Ergebnis wie vorheriges Modell, bietet aber noch den Zugriff auf das Beschleunigungssignal.
| Differentialgleichung:
|
v = Geschwindigkeit v’= Beschleunigung (Ableitung von v) K = Übertragungsmaß T = Zeitkonstante U = Eingangsgröße (z.B. Spannung) |
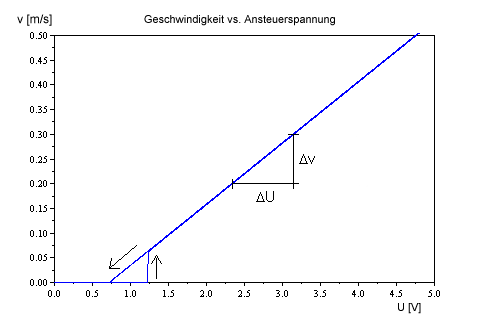
Die beiden Parameter K und T müssen ausgemessen werden, wenn sie nicht bekannt sind. Die Zeitkonstante T kann in einem Anlaufversuch ermittelt werden. Dazu wird auf den Motor ein Spannungssprung gegeben und die Sprungantwort am Ausgang nachgemessen. Bei einem Antrieb erspart diese Methode die aufwändige Ermittlung der elektrischen und mechanischen Daten der einzelnen Elemente (Motor, Getriebe, Fahrzeug). Bei der Ermittlung des Übertragungsmaß K ist zu beachten, dass sich möglicherweise der Motor durch starke Reibung erst ab einer bestimmten Spannung dreht. Hier ist die Steigung der Kennlinie mit delta v / delta U auszuwerten, wie im folgenden Bild zu sehen ist.
Die einfachen Modelle gelten nur für den linearen Teil der Kennlinie. Soll auch die Nichtlinearität durch Reibung modelliert werden, dann sind detailliertere Modelle, wie im Folgenden beschrieben, zu verwenden. Die Auswirkung einer Haftreibung ist auch in dem Geschwindigkeitsdiagramm durch die Hysterese in der Kennlinie zu sehen. Beim Hochfahren der Ansteuerspannung bewegt sich das Fahrzeug erst ab ca. 1.25V, während beim Herunterfahren der Ansteuerspannung das Fahrzeug noch bis 0.75V rollt und erst unter 0.75V stehen bleibt.
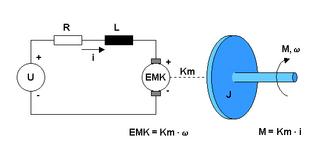
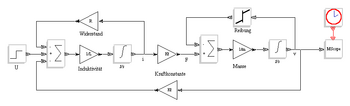
Detailliertes Modell
Ein detailliertes Motormodell ist rechts in dem Bild zu sehen. Es hat auf der linken Seite den elektrischen Teil mit den Parametern R (Widerstand) und L (Induktivität) und auf der rechten Seite den mechanischen Teil mit den Blöcken Trägheitsmoment und Reibung. Der elektrische Teil liefert das Stromsignal i, welches mit der Motorkonstante Km in das Drehmoment M umgerechnet wird. Mit dem folgenden Summierglied kann über einen zusätzlichen Eingang auch ein extern angreifendes Lastmoment mit simuliert werden. Am Ausgang des mechanischen Teils steht die Winkelgeschwindigkeit w in der Einheit [rad/s] bzw. über den Umrechnungsfaktor 9.55 die Drehzahl in [Upm] zur Verfügung. Die Reibung wird in einem nichtlinearen Block mittels Lookup-Table simuliert. In der einschlägigen Literatur wird die Reibung meistens mit einem Dämpfungsfaktor (linear) simuliert, was einer viskosen Reibung entspricht. Das passt aber nicht so gut für Kleinmotoren, da überwiegt vor allem die trockene Reibung. Die trockene Reibung hat ein konstantes Bremsmoment wenn sich der Motor dreht (unabhängig von Drehzahl, Vorzeichen abhängig von Drehrichtung). So eine Funktion kann sehr einfach mit einer Lookup-Table realisiert werden. Die Lookup-Table kann auch dazu verwendet werden, Mischformen von trockener, viskoser und turbulenter Reibung und sogar noch Haftreibung in einem Block zu simulieren, wenn man will.
Bei einigen Herstellern, wie z.B. Faulhaber und Maxon, kann man die für das Modell nötigen Parameter im Datenblatt finden. Das Bremsmoment der Reibung berechnet sich aus dem Leerlaufstrom wie folgt: Bremsmoment = Motorkonstante * Leerlaufstrom
Falls die Daten nicht verfügbar sind, muss man sie selbst ausmessen. Eine Hilfestellung zur Bestimmung der Motorkonstante und des Trägheitsmoments gibt es hier:
- http://www.roboternetz.de/phpBB2/zeigebeitrag.php?p=96750&highlight=#96750
- http://www.roboternetz.de/phpBB2/viewtopic.php?t=12793
Das detaillierte Motormodell kann auch für einen Antrieb verwendet werden, wenn man eine starre Kopplung zwischen Motor und Antriebsrad voraussetzt, also Elastizität und Spiel des Getriebes vernachlässigt. Anstelle der rotatorischen Kenngrößen (Drehmoment M, Trägheitsmoment J, Winkelgeschwindigkeit w) werden die translatorischen Kenngrößen (Kraft F, Masse m, Geschwindigkeit v) eingesetzt. Das Drehmoment wird mittels Getriebeübersetzung ü und Radius r des Antriebsrades in die entsprechende Vortriebskraft umgerechnet. Daraus ergibt sich die Kraftkonstante Kf, die für das Antriebsmodell verwendet wird.
Die Umrechnung ist: Kf = Km * ü/r
Bei der Trägheitsmasse m muss neben der Masse des Fahrzeugs auch das Trägheitsmoment des Motors mit berücksichtigt werden. Die Umrechnung von Trägheitsmoment in eine äquivalente Masse = J * (ü/r)²
Der Reibungsblock in diesem Modellbeispiel enthält eine Mischform aus Haftreibung, trockener und viskoser Reibung, wie sie typisch für einen Kleinbot mit 2 Antriebsrädern und einem Gleitpin ist.
Beispiel: Drehzahlregelung
Es wird ein Gleichstrommotor in der Drehzahl geregelt. Als Sensor ist ein Tachogenerator vorhanden, der direkt auf der Motorwelle sitzt. Das System ist in einem kleinen Modellfahrzeug eingebaut und wird zur Geschwindigkeitsregelung eingesetzt, da die Drehzahl proportional zur Geschwindigkeit ist.
Das Funktionsschaltbild sieht folgendermaßen aus:
http://www.roboternetz.de/wiki/uploads/Main/drehzahl1.gif
Als Störgröße können unterschiedliche Reibwerte oder Steigung und Gefälle rückwirkend über das Getriebe die Drehzahl beeinflussen. Das Getriebe und die Last sind zwar außerhalb der Regelschleife, beeinflussen aber durch die feste Kopplung des Getriebes die Dynamik des Regelkreises. Durch die starre Kopplung kann das Trägheitsmoment des Motors und die Masse des Fahrzeugs zusammengefasst werden. Das Gleiche gilt auch für die Reibwerte. Damit vereinfacht sich die Modellierung und das Blockschaltbild reduziert sich auf folgende Schaltung:
http://www.roboternetz.de/wiki/uploads/Main/drehzahl2.gif
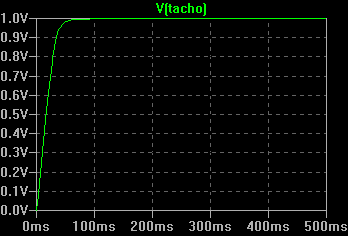
Zur Ermittlung des dynamischen Verhaltens der Regelstrecke wird die Sprungantwort gemessen. Dazu wird auf den Eingang der Regelstrecke (Stellglied) ein Spannungssprung gegeben und die Antwort am Ausgang des Tachogenerators nachgemessen. Diese Methode erspart die aufwändige Ermittlung der elektrischen und mechanischen Daten der einzelnen Elemente der Regelstrecke (Motor, Getriebe, Fahrzeug). Die Messung ergab folgende Sprungantwort der Regelstrecke:
http://www.roboternetz.de/wiki/uploads/Main/tacho.gif
Wie zu erwarten, ist die Sprungantwort annähernd ein Verzögerungsglied 1.Ordnung. Die abgelesene Zeitkonstante ist 0.11s. Die Verstärkung der Regelstrecke ist Ks = 0.72. Das Übertragungsmaß des Tachogenerators ist 1V pro 2480Upm. Damit kann auf die Drehzahl rückgerechnet werden.
Da die Regelstrecke nur aus einem PT1-Glied besteht, könnte eine analoge Regelung fast beliebig schnell gemacht werden. Wegen der Begrenzung bringt aber das Ausreizen der Optimierung für das Führungsverhalten nicht viel, nur für das Störverhalten wäre eine schnellere Regelung sinnvoll. Um aber einen Vergleich zwischen analogem und digitalem Regler anstellen zu können wird eine Parametrierung gewählt, die auch für den digitalen Regler mit seiner Totzeit noch stabil ist. Es wird deshalb auch auf einen D-Anteil im Regler verzichtet und nur ein PI-Regler realisiert. Das vereinfachte Blockschaltbild mit den dynamischen Elementen sieht damit folgendermaßen aus:
http://www.roboternetz.de/wiki/uploads/Main/drehzahl3.gif
Zur Veranschaulichung wurde ein analoger als auch ein digitaler Regler realisiert. Die Parametrierung des analogen Reglers wurde mit dem Programm LTspice durchgeführt. Es bot sich an, da die analoge Reglerschaltung exakt simuliert werden konnte. Für die Optimierung des digitalen Reglers wurde dann Scicos verwendet.
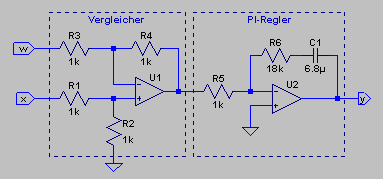
Realisierung mit analogem Regler
Die elektrische Schaltung für einen analogen PI-Regler ist in der nächsten Abbildung zu sehen. Der erste Operationsverstärker vergleicht den Sollwert w mit dem Istwert x. Der zweite Operationsverstärker bildet den PI-Regler. Die Werte R5, R6 und C1 sind für die Charakteristik des PI-Reglers zuständig. Mit R6 kann der P-Anteil und mit C1 der I-Anteil eingestellt werden. Die Optimierung der Werte wurde empirisch in einer Simulation mit LTspice durchgeführt. Da die Schaltung des PI-Reglers invertiert, wurden zum Ausgleich am Vergleicher die Eingänge an U1 vertauscht, so dass sich über die gesamte Schaltung wieder die richtige Polarität ergibt.
Zum Umrechnen auf Kp und Ki können diese Formeln verwendet werden, siehe auch PI-Regler:
Kp = R6/R5 = 18
Ki = 1/(R5*C1) = 147
Realisierung mit digitalem Regler
Im digitalen Regelkreis wird der Istwert x vom Tachogenerator mit einem A/D-Wandler digitalisiert. Der Sollwert w wird dem µC als digitaler Wert übergeben. Die Stellgröße y entspricht dem PWM-Wert für den Motortreiber. Um zum analogen Regler vergleichbar zu sein, wurde sowohl für den A/D-Wandler als auch für den PWM-Steller eine 8-Bit-Breite vorgesehen. Damit ist die Verstärkung in beiden Fällen gleich und analoger und digitaler Regler besser vergleichbar.
Eigentlich könnte man bei kleiner Abtastzeit direkt die Parametrierung des analogen Reglers für die digitale Realisierung übernehmen. Aber es gibt doch kleine Unterschiede in der Dynamik zwischen analoger und digitaler Ausführung und um sicher zu gehen, dass die gewählte Abtastzeit einen nicht zu großen Einfluss hat, wird noch einmal mit Scicos nachoptimiert. Mit einer Abtastzeit Ta = 10ms und den Parametern des analogen Reglers ergibt sich ein Überschwingen, das nur sehr langsam auf den Endwert abklingt. Durch Verringern des I-Anteils auf 60 wird ein optimales Einschwingen für den digitalen Regler erreicht. Die Parameter sind:
Kp = 18
Ki = 60
Ta = 0.01
Zur Umsetzung in einen Code wurde die Programmiersprache C gewählt. Da der Code sehr einfach ist, sollte es auch kein Problem sein, den Code als Beispiel für andere Sprachen zu verwenden. Der Algorithmus wird im Takt der Abtastzeit, also alle 10ms aufgerufen. In der Reglergleichung kann zur Vereinfachung das Produkt Ki*Ta durch eine Ersatzvariable, die gleich das Ergebnis aus dem Produkt 60*0.01 = 0.6 hat, ersetzt werden. Zum besseren Verständnis wurde es hier beim Ki*Ta belassen. Um einen Windup-Effekt zu verhindern, wird die Summenbildung esum auf +-400 begrenzt. Der Wert wurde so gewählt, dass noch eine volle Aussteuerung durch den I-Anteil möglich ist. Zum Schluss wird die Stellgröße y auf die mögliche Aussteuerung des Stellglieds (0...255) begrenzt.
Programmbeispiel digitaler PI-Regler:
e = w - x; //Vergleich
esum = esum + e; //Integration I-Anteil
if (esum < -400) {esum = -400;} //Begrenzung I-Anteil
if (esum > 400) {esum = 400;}
y = Kp*e + Ki*Ta*esum; //Reglergleichung
if (y < 0) {y = 0;} //Begrenzung Stellgröße
if (y > 255) {y = 255;}
PWM = y; //Übergabe Stellgröße
Beispiel: Lageregelung
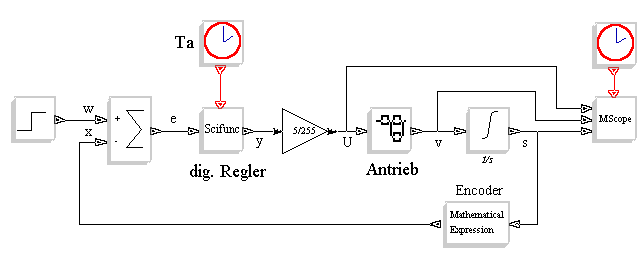
Unter einer Lageregelung versteht man die Positionierung von Objekten. Als Beispiel soll hier ein kleiner Bot mit Radencoder eine bestimmte Weglänge fahren. Gegenüber der Drehzahl- oder Geschwindigkeitsregelung ist bei der Lageregelung noch ein zusätzlicher Integrator in der Strecke vorhanden. Die gesamte Strecke ist damit ein I-Glied mit Verzögerung. Laut Tabelle im Abschnitt „Dimensionierung des Reglers“ ist dafür ein PD-Regler gut geeignet. Der PD-Regler wird digital ausgeführt, zur Simulation und Parametrierung bietet sich deshalb Scicos an.
Da bei einer Lageregelung der Geschwindigkeitsbereich von Null aus geht, also über den nichtlinearen Bereich geht, sollte auch in der Simulation die Nichtlinearität berücksichtigt sein. Für das Beispiel wird deshalb das Modell eines Antriebs mit Haft- und Gleitreibung genommen, wie es unter "Modellierung eines Antriebs – detailliertes Modell" bereits vorgestellt wurde. Im Scicos-Modell ist der Antrieb der Übersichtlichkeit wegen als Superblock ausgeführt. Das Blockschaltbild des Antriebs im Detail ist hier zu sehen. Die Daten sind:
R = 16 Ohm; L = 6 mH; m = 0.31 kg; Kf = 6.6 N/A
Als Sensor kommt ein Inkrementalgeber zum Einsatz, allerdings muss der richtungssensibel sein, sonst ist keine Lageregelung möglich. Der Sensor wird in Scicos mit der Rundungsformel (round(u1*500)) simuliert. Das ergibt bei einer Auflösung von 2mm ganzzahlige Schritte, wie es auch die Hardware (Inkrementalgeber mit nachfolgendem Zähler) in Wirklichkeit macht.
Nach dem Regler folgt ein Block mit der Verstärkung (5/255), der den PWM-Wert auf die Ansteuerspannung für den Motor umsetzt. Der Bruch 5/255 entspricht der Ansteuerspannung von 5V bei PWM=255. Der PD-Regler kann damit in Scicos exakt so simuliert werden, wie er schlussendlich auch als C-Code umgesetzt wird. Dazu wird der Code des PD-Reglers als Funktion in den Scifunc-Block eingegeben. Der Code ist etwas unterschiedlich zum C-Code des realen Bots, da die Syntax in Scicos doch geringfügig anders ist und die Eingangs- und Ausgangsvariablen nur bestimmte Bezeichnungen haben dürfen. Im nachfolgenden Codefenster sind beide Varianten im Vergleich zu sehen.
Scifunc-Code:
y1=Kp*u1+Kd/Ta*(u1-z); z=u1; if y1>255 then y1=255; end if y1<-255 then y1=-255; end |
C-Code für µC:
e = w - x;
y = Kp*e + Kd/Ta*(e-ealt);
ealt = e;
if (y > 255) {
y = 255;
}
if (y < -255) {
y = -255;
}
|
Kommentar:
Vergleich PD-Reglergleichung alten Wert speichern pos. Begrenzung neg. Begrenzung |
In der praktischen Umsetzung des C-Codes wird man den Bruch Kd/Ta durch eine Ersatzvariable oder Konstante ersetzen. Dabei ergibt sich (wie in diesem Beispiel 2/0.01 = 200) meistens ein ganzzahliger Wert, was sich positiv auf die Rechenzeit auswirkt.
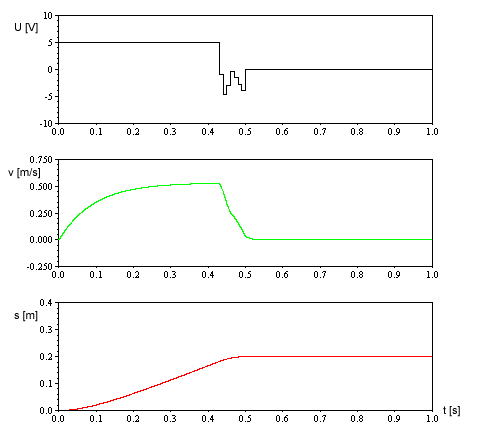
Für die Abtastzeit Ta wurde 10ms gewählt. Das ist einerseits nicht zu schnell für einen µC und andererseits nicht zu lang, um die Regelung unnötig zu verlangsamen. Die Parametrierung von Kp und Kd erfolgte empirisch durch Probieren in der Simulation. Begonnen wurde mit einem reinen P-Regler und kleinem P-Anteil (Kp=1, Kd=0). In groben Schritten wurde Kp solange erhöht, bis sich deutlich Überschwinger zeigten. Dann wurde ein D-Anteil hinzugefügt und Kd so variiert, dass der Überschwinger verschwindet. Mit ein bisschen Feintuning ergaben sich so die Werte Kp=61 und Kd=2. Das Simulationsergebnis für Ansteuerspannung, Geschwindigkeit und Weg sieht damit folgendermaßen aus:
Autoren
Siehe auch
External links
- Post: Line follower with PID controller
- Scicos Homepage
- ScicosLab Homepage
- Scilab Homepage
- LTspice / SwitcherCAD III Download
- set_download.php demo version of WinFACT 7
- instructions for electronic placement, the last part is based PID controller
- SimApp website with trial
- ExpertControl Homepage, Automatische Reglerauslegung mit ecICP ecICP-Trial über Support-Seite verfügbar