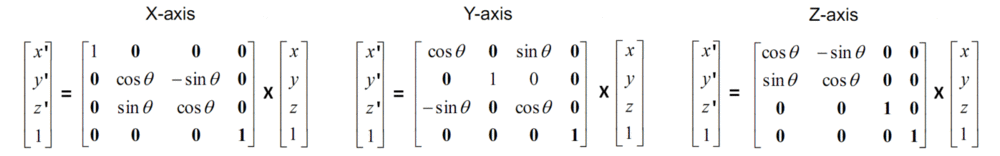Inhaltsverzeichnis
- 1 Kinematics of Serial Robotics
- 2 Dynamik und Kinematik
- 3 Begriffe & Philosophie
- 4 Direkte Kinematik
- 5 Inverse Kinematik
- 6 Linearität und Oberwelle
- 7 Bézier Kurven & Bahngenerator
- 8 Labyrinth von Chartres
- 9 Kollision
- 10 Von der Theorie zur Praxis
- 11 Weblinks
Kinematics of Serial Robotics
Algorithms for simplified calculation of Direct & Inverse Kinematics in a Consistent Coordinate Reference system
Seit ich die Erstausgabe dieses Textes bei RN-Wissen veröffentlichte sind einige Jahre vergangen. Inzwischen habe ich eine neuartige Mathematik der Roboter-Kinematik entwickelt und im Rahmen des
- AHFE-Symposiums 2023
- Application of Emerging Technologies: Robotics and Automation II
in englischer Sprache als Conference Paper
- Kinematics of Serial Robotics – Algorithms for simplified calculation of Direct & Inverse Kinematics in a Consistent Coordinate Reference system
DOI: http://doi.org/10.54941/ahfe1004416 / http://dx.doi.org/10.54941/ahfe1004416
vorgestellt.
- Die Veröffentlichung ist OpenAcess und somit als PDF frei zugänglich.
- PowerPoint Audio-Video Präsentation
https://video.ibm.com/recorded/133181477 / https://video.ibm.com/playlist/672378
Vorwort
Irgendwie hatte sich aus Diskussionen zur Knickarm-Robotermechanik die Frage ergeben, …"und wie berechnen Sie das?" Meine Antwort war, "Mit EXCEL® ist das recht einfach." Ganz so einfach war es dann doch nicht.
Im Internet findet sich zwar einiges zum Thema, aber wenig Problem orientiertes im Focus Robotic. Meine Recherchen führten mich so zunächst in die Entwicklung Robotic orientierter Algorithmen.
- Entstanden ist hieraus ein Mathematischer 3D-Gelenk-Baukasten. Eine kostenlose Test und Demo-Version erhalten Sie im Download von meiner Web-Site.
- Hier, im Teil 1 finden Sie Hintergrundinformation zu Problemen der Kinematik, konkurrierende Lösungsansätze und die Mathematik der Winkeltransformation in einem eher theoretischen Focus (Tutorial). Mit einigen Links verweise ich auf diejenigen, von denen ich "Honig gesaugt" habe. Alle externen Links sind offen mit ihrer URL im Kontext dieses Artikels ausgewiesen und nicht hinter einem Pseudonym versteckt. – Clicken muß man sie nur, um in die Tiefe zu gehen!
- Die Theorie wird im Praxis orientierten Teil 2 ergänzt. Inverse Kinematik 2 – Praxis. Besprochen werden ein 3D-Bahngenerator und die aus der "Sollbahn" berechneten Winkel der Knickarme.
Dynamik und Kinematik
beschreiben "wie sich was" bewegt;
- die Dynamik fokussiert auf Beschleunigung und Verzögerung einer Bewegung unter Einfluß einer kontinuierlichen oder sich zeitlich ändernden Kraft;
- die Kinematik berechnet "was sich wie" bewegt – ohne die Ursache, also die einflußnehmende Kraft zu betrachten.
Wenngleich die Begriffe in einander zahnen, ist jeder für sich - zumindest theoretisch - ohne den anderen betrachtbar. Diese Arbeit befaßt sich mit der Kinematik von Roboterarmen und deren Berechnung.
Zur Einstimmung legen wir unsere Hand auf eine Tischkante und bewegen Sie nach vorn - und wir beobachten bewußt, wie sich hierbei Schultergelenk, Ellenbogen- und Handgelenk mit unterschiedlicher Winkelgeschwindigkeit bewegen. Als Kleinkind haben wir Kinematik über Jahre studiert, wir haben gelernt uns zu bewegen und wir haben sogar inverse Kinematik studiert: Letztendlich interessiert nicht, wohin die Hand sich bewegt, wenn Gelenke einen definierten Winkelwert einnehmen; wir wollen nicht irgendwelche Muskeln oder Gelenke bewegen, sondern "den Finger in die Nase stecken – und bohren"!
Entsprechend dem Ausgangs- und Zielwert bzw. seiner Algorithmen unterscheidet sich Kinematik in
- Direkte Kinematik – auch als "vorwärts"-Kinematik bezeichnet
- (welcher Raumpunkt wird erreicht, wenn Länge und Winkel der Knickarme geben sind) und
- Inverse Kinematik – "umgekehrte"-Kinematik
- (welche Länge und Winkel der Knickarme werden erforderlich, um einen gegebenen Raumpunkt zu erreichen).
Legen wir die Hand am ausgestreckten Arm flach auf den Tisch, so können wir Ober- und Unterarm drehen ohne das sich die Hand bewegt – dieses Phänomen der Inversen Kinematik wird uns noch jede Menge Ärger machen – und ist eine Herausforderung an die Mathematik.
Begrenzt wird Kinematik vom Freiheitsgrad der Gelenke und der steuernden Intelligenz. Soll ein Roboter-Arm übernehmen, was wir als Kleinkind erlernt haben, so erfordert dies eine anspruchsvolle Bahnsteuerung – und einige Mathematik.
Begriffe & Philosophie
Drehachse & Schwenkachse
Unterschieden wird in der Robotik oftmals der Begriff "Drehachse und Schwenkachse". Aus Sicht der Kinematik gibt es diesen Unterschied nicht. Eine Schwenkachse wird letztendlich von einer in der Bewegungs-Kaskade seriell davor liegenden Achse gedreht. Aus Anwendersicht ist die Definitionsunterscheidung trotzdem sinnvoll!
Fußpunkt, Ellenbogen & Co
Auch diese, den menschlichen Extremitäten nachempfundene Begriffe finden wir in der Literatur. Fußpunkt mag zunächst plausibel erscheinen. Beim Roboter ist der Fußpunkt unbeweglich, beim Menschen Basis aller Bewegungen. Wenn die Begriffe Ellenbogen und Handgelenk sinnvoll sein sollen, dann ist der Fußpunkt in Konsequenz eher "Schulter"! - Fußpunkt macht hingegen Sinn, falls der Roboter auf Portal verfahrbar ist.
Philosophie eines mathematischen Ansatzes
Der RoBo-mac Gelenk-Baukasten unterscheidet dementsprechend für die Vorwärts Kinematik keine Dreh- und Schwenkachsen.
- Die Kinematik wird durch Parametrierung der Achs-Länge, Ihrer XYZ-Orientierung und des max. Achs-Drehwinkels definiert.
- An- und Abtrieb jedes Gelenkes kann unter beliebigem Winkel im Raum stehen.
- Einige High-End Roboter arbeiten mit Teleskop-Armen, der mathematische Gelenk-Baukasten beherrscht auch diese Konstruktionen.
- Der Algorithmus ermöglicht beliebig viel kaskadierbare Teleskop-Dreh Achsen.
In Anlehnung an die 8-Achsen Bahnsteuerung RoBo-mac's enthält der Gelenk-Baukasten 8 Achsen mit jeweils 2 Freiheitsgraden (Teleskop-Dreh Achse).
Definitionsgemäß führt die Null-Position aller Dreh-Gelenke zu einer kaskadierten Streckung aller Achs-Elemente; bei Bodenbefestigung entspricht dies "senkrecht nach oben". Wird der Arm an einem (beweglichen) Portal befestigt, so ergeben sich bei Null-Position der Gelenke ggf. andere Ausrichtungen im 3D-Raum, die der RoBo-mac Gelenk-Baukasten berücksichtigt.
Mathematiker und Ingenieure leben in verschiedenen Welten! Einig sind sich beide, daß die X-Achse grafisch von links nach rechts laufend dargestellt wird, bei Y- und Z- scheiden sich die Geister:
- Mathematiker stellen die Y-Achse grafisch gerne senkrecht, die Z-Achse "perspektivisch schräg nach hinten bzw. vorne" laufend dar.
- - Dies ist die logische Erweiterung eines 2D Systems zu einem in der Ebene dargestellten 3D-System
- CAD- & Grafik-Programmen liegt meist diese Definition des Weltkoordinatensystems zu Grunde, vgl.: http://www.3dsource.de/deutsch/3Dmathe.htm
- - Im Ingenieurwesen wird andererseits die senkrechte Achse oftmals mit "Z" bezeichnet – was in eine gewisse Verwirrung führt.
- Im Ergebnis ist es gleich, ob nun die Y- oder die Z-Achse als Senkrechte definiert wird.
- - Beide Systeme sind durch Drehung um die X-Achse ineinander gegenseitig abbildbar.
Wichtig ist die Systemdurchgängigkeit und wichtig ist vor allem, ob es sich um ein 'rechts-' oder ein 'links'-System handelt:
- Im rechtshändigen Weltkoordinatensystem zeigt (für jeweils positive Koordinaten) die X-Achse nach rechts, die Y-Achse nach oben und die Z-Achse aus der Zeichenebene heraus - nach vorne.
- Im linkshändigen System hingegen zeigt sie nach hinten! - Dies entspricht einer Spiegelung bzw. Drehrichtungsumkehr.
Der Mathematik des Gelenk-Baukastens liegt die Definition des Weltkoordinatensystems zu Grunde; RoBo-mac bietet die Umschaltmöglichkeit zwischen rechts- und linkshändischem Koordinatensystem, die Achs-Bezeichnug der Ein- und Ausgabewerte Y- / Z- ist ergänzend umschaltbar. Unter '3D-Transformation & 2D-Perspektive' betrachten wir das Thema nochmals im Focus 'Verdrehte Koordinatenwelt' (vgl. 3.1.3 und 3.1.4) !
Arbeitsbereich
Die Mechanik der Achsen (Länge und Winkelbeweglichkeit) begrenzt den Arbeitsbereich, einige Konstruktionen überstreichen einen Winkelbereich von mehr als +/- 180° je Achse, andere liegen (knapp) darunter. Im einfachsten (mechanisch nicht möglichen) Fall wäre der Arbeitsbereich eine exakte Kugel mit dem Radius aller gestreckten Achsen und dem Roboter Schulterpunkt in der Mitte, defacto gleicht die "Kugel" eher einem "Apfel".
Bei einigen Konstruktionen (KUKA / …) schneidet die Schwenkachse des dem Schulterpunkt nächsten Arms die theoretische (senkrechte) Drehachse nicht mittig, sondern rotiert auf einer Kreisbahn um diese herum, diese Auskragung hat also bereits Einfluß auf die X- und Z-Koordinaten (Achs-Definition: Weltkoordinatensystem); andere Konstruktionen (Stäubli / ...) arbeiten mit zentrischer Schulterpunkt-Achse; beide Bauarten sind parametrierbar. Im Handbuch wird dies als Supervisor-Information erläutert.
Visuelle Kontrolle (Adler & Maus Perspektive)
Unabhängig von der räumlichen XYZ Erfassung und Berechnung der Gelenk-Winkel ermöglicht es eine zusätzliche Perspektivische Betrachtung (aus beliebiger Position), "Tiefe" in der Ebene möglichst plausibel darzustellen – oder die (mathematisch "positive") CCW Drehrichtung entsprechend den Schieberbewegungen "im Uhrzeigersinn" (CW) zu visualisieren. Der hier verwendete Algorithmus wird im Rahmen der direkten Kinematik zunächst besprochen:
Direkte Kinematik
Die Mathematik geht auf simple Winkelberechnung und ihre Klassiker, Sinus / Cosinus / Tangens zurück. Unter http://de.wikipedia.org/wiki/Eulersche_Winkel findet sich eine Einführung in die Theorie der Winkeltransformation, näher beschrieben werden die Abhängigkeiten in: http://www-lehre.inf.uos.de/~cg/2006/PDF/kap-13.pdf und http://www.cg.tuwien.ac.at/courses/CG1/textblaetter/02%20Geometrische%20Transformationen.pdf.
Ich will versuchen, die letztendlich doch recht komplexen Winkelbeziehungen hier vereinfacht zu beleuchten. Grundsätzlich gilt:
- Die Winkellage eines Punktes in der Ebene wird im XY-Koordinatensystem,
- die eines Punktes im Raum im XYZ-Koordinatensystem beschrieben.
- Legt man das willkürlich gelegte Koordinatensystem "anders", so beschreiben "andere" Koordinatenwerte ebenfalls die Lage des Punktes präzise.
Die Winkeltransformation ermöglicht es, die Winkel-Werte des einen Koordinatensystems in das andere zu transferieren. Bildlich gesehen wird hierzu das Koordinatensystem "gedreht, verschoben und skaliert".
- Einen Punkt in der Ebene zu verschieben ist einfach
- Zu den XY-Koordinaten des Original-Punktes werden X und Y Wert addiert, bei der Skalierung werden die XY-Koordinaten mit einem Skalierungsfaktor multipliziert; bitte beachten:
- Eine unterschiedliche Reihenfolge der Transformationsschritte führt bereits bei dieser einfachen Aufgabe zu unterschiedlichen Ergebnissen!
- Den Punkt um eine Achse zu drehen, ist selbst in der Ebene etwas komplexer:
- Die Transformationsgleichungen lauten für ein Winkeldrehung um '[math] \theta \ [/math]':
- x' = x • cos([math] \theta\ [/math]) − y • sin([math] \theta\ [/math]) bzw. x = x' • cos([math] \theta\ [/math]) + y' • sin([math] \theta\ [/math])
- y' = x • sin([math] \theta\ [/math]) + y • cos([math] \theta\ [/math]) bzw. y = -x' • sin([math] \theta\ [/math]) + y' • cos([math] \theta\ [/math])
- Die Drehrichtung ist also reversierbar.
- Gedreht wurde um die Z-Achse.
Hier die erste wichtige Erkenntnis:
- An der Drehung um die Z-Achse sind nur die XY-Koordinaten beteiligt.
Natürlich läßt sich eine zweidimensionale Darstellung auch um die X- bzw. Y-Achse drehen. Wird um die X Achse gedreht, so verkürzen sich die Y-Werte, wird um Y gedreht, die X-Werte (um jeweils den Cosinus des Drehwinkels). Ob dies sinnvoll ist, sei dahingestellt.
Liegt ein Punkt nicht in der Ebene, sondern im Raum, so hat er eine zusätzliche Koordinate, die Z-Koordinate. Die Zeichnerische Darstellung ist etwas komplex, da ja in der Ebene keine "Tiefe" dargestellt werden kann. In der klassischen Konstruktionslehre wurden 3 Ansichten (Frontsicht, Seitenansicht, Draufsicht) gezeichnet, und der "Technische Zeichner" erlernte Methoden, hieraus eine Perspektivische Ansicht zu erstellen – heute macht das der PC!
Wird ein in der Tiefe liegender Punkt um X oder Y gedreht, so führt die Transformation "aus der Tiefe in die Ebene" nicht nur zur Änderung seiner Z-Koordinate, sondern auch zur Änderung seiner XY-Koordinaten. Es gilt
- für die X-Achse
- x' = x
- y' = y • cos([math] \theta\ [/math]) −z • sin([math] \theta\ [/math])
- z' = y • sin([math] \theta\ [/math]) +z • cos([math] \theta\ [/math])
- für die Y-Achse
- x' = z • sin([math] \theta\ [/math]) +x • cos([math] \theta\ [/math])
- y' = y
- z' = z • cos([math] \theta\ [/math]) −x • sin([math] \theta\ [/math])
Hier die zweite wichtige Erkenntnis:
- Bei Drehung um eine beliebige Koordinaten-Achse ändern sich die Koordinaten der jeweiligen Dreh-Achse nicht!
Basierend auf diesen Kenntnissen können wir "zu Fuß" jeden beliebigen Raum-Punkt transferieren, dies ist zugegebener Maßen etwas mühselig.
Transformation & Matrizenrechnung
Die Mathematik bedient sich für die Transformation meist der Matrizenrechnung, sie ist – beginnend mit ihrer Schreibweise – etwas gewöhnungsbedürftig; in Kurzform:
Eine Matrix besteht aus Zeilen und Spalten, die eine Tabelle bilden; die Matrizenrechnung verknüpft nach einem definierten Verfahren mindestens 2 Matrizen (Mehrzahl von Matrix) und erzeugt im Ergebnis eine neue Matrix. In der visuellen Darstellung wird meist jede Matrix für sich mit einer alle Zeilen übergreifenden Klammer "gerahmt", zwischen den Matrizen befindet sich der mathematische Operator.
Die Matrizenrechnung ist eigentlich nur eine "andere", sehr formale Darstellungsart bekannter Mathematik. Der Matrizen-Formalismus führt (nach Eingewöhnung) in eine sehr übersichtliche Darstellung, insbesondere "wenn vieles mit vielem" verknüpft werden muß; manchmal erkennt man am Matrix-Aufbau bereits was sie bewirkt!
Matrizenmultiplikation
Die Ergebnismatrix der Matrizenmultiplikation erhält die Zeilenzahl der ersten und die Spaltenzahl der zweiten Matrix, wesentliche Voraussetzung: Die Spaltenzahl der ersten Matrix muß gleich der Zeilenzahl der zweiten Matrix sein, (sonst geht es nicht)!
- – aber Zeilenzahl der ersten Matrix und Spaltenzahl der zweiten sind beliebig!
- – Als Sonderfall sind beide Werte gleich (Quadratische-Matrix).
Die Rechenanweisung der Matrizenmultiplikation lautet für die
- Ergebnismatrix "Zeile 1 der Spalte 1".
- - Multipliziere das Element aus Matrix 1 "Zeile 1 der Spalte 1" mit dem Element aus Matrix 2 "Zeile 1 der Spalte 1"
- - Multipliziere das Element aus Matrix 1 "Zeile 1 der Spalte 2" mit dem Element aus Matrix 2 "Zeile 2 der Spalte 1"
- - Multipliziere das Element aus Matrix 1 "Zeile 1 der Spalte 3" mit dem Element aus Matrix 2 "Zeile 3 der Spalte 1" usw.;
- - addiere die Einzelergebnisse und schreibe deren Summe in die Ergebnismatrix "Zeile 1 der Spalte 1".
- Für die Ergebnismatrix "Zeile 1 der Spalte 2" gilt gleichsinnig:
- - Multipliziere das Element aus Matrix 1 "Zeile 1 der Spalte 1" mit dem Element aus Matrix 2 "Zeile 1 der Spalte 2"
- - Multipliziere das Element aus Matrix 1 "Zeile 1 der Spalte 2" mit dem Element aus Matrix 2 "Zeile 2 der Spalte 2"; usw.
Jeder Zeilenvektor der ersten Matrix wird also unabhängig von allen anderen Zeilen dieser Matrix elementweise mit allen zugehörigen Spaltenvektoren der zweiten Matrix multipliziert. Es "paaren" also die Zeilen-Elemente je Spalte mit den Spalten-Elementen der korrespondierenden Zeilen. Die Einzelwerte der Ergebnismatrix hängen somit (selbst bei gleicher Zeilen und Spaltenzahl) von der Reihenfolge der Eingangs-Matrizen ab!
- Eine quadratische Matrix 3 x 3 erfordert also z. B. 3³ = 27 Einzelmultiplikationen.
Hier die dritte wichtige Erkenntnis:
- Die Reihenfolge der Matrizenmultiplikation bestimmt das Ergebnis.
- Eine Vertauschung der Matrizenreihenfolge führt zu unterschiedlichem Ergebnis.
Vektortransformation & Homogene Koordinaten
Die gradlinige Verbindung zweier Punkte im Raum wird auch als Vektor bezeichnet. Jeder Vektor hat eine Größe (Länge) und eine Winkelausrichtung gegenüber dem Koordinatensystem. Vektoren haben somit einen Start- und einen Ziel-Punkt, der wahlweise mit Länge und Winkel (polar) bzw. seinen Start- und Ziel-Koordinaten (XYZ) beschrieben wird.
Bezogen auf die Roboter-Kinematik wird für die Bewegungsanalyse jeder Vektor für sich in einen anderen Vektor transformiert, dies übernimmt die Transformationsmatrix, die achsenspezifisch nach jeweils unterschiedlichem Schema aufgebaut ist;
- sie enthält die Sinus und Cosinus Werte der Drehachse, die "Leerstellen" sind mit "Nullen und Einsen" besetzt.
Auffällig in diesen Schemata ist, daß für eine 3D-Transformation nicht 3 Zeilen und 3 Spalten, sondern jeweils 4 verwendet werden, die in der letzten Spalte und untersten Zeile zusätzliche "Nullen", sowie im Kreuzungspunkt eine "Eins" aufweisen.
- Während die Rotation mit den Regeln der Matrizenmultiplikation errechnet wird, erfordert die Verschiebung, eine Vektoraddition, also unterschiedliche Rechenoperationen.
- Durch Hinzufügen einer zusätzlichen Spalte und Zeile, den "Homogenen Koordinaten" kann die zusätzliche Vektoraddition in die Matrizenmultiplikation integriert werden. Die Verschiebung um XYZ wird dann als "Translationswert" in der Matrix an Stelle der Nullen eingetragen.
Ich hatte behauptet, der Matrizen-Formalismus führe in eine sehr übersichtliche Darstellung:
- Ohne die "Homogenen Koordinaten" besteht jede der (Quadratischen) Rotations-Matrizen aus 3 Zeilen und 3 Spalten, also 9 Elementen. Dies sind eine "Eins", vier "Nullen" sowie die sin/cos Werte. Die "Eins" kennzeichnet die Koordinate, um die gedreht wird! (vgl. Zweite Erkenntnis)!
- Wird diese "Eins" zu "-1" negiert, so wird die Achse gespiegelt!
Mathematiker und Ingenieure leben in getrennten Welten! – Wir hatten das Thema bereits.
- Die meisten Veröffentlichungen zum Thema stammen aus mathematischer Fakultät. Wir wissen bereits, daß ein Roboterglied mathematisch als Vektor betrachtet werden kann und mit seinen XYZ-Koordinaten beschrieben wird.
- Mathematiker schreiben die XYZ-Koordinaten eines Vektors meist untereinander (vgl. Tabelle oben)
- Ingenieure bevorzugen die horizontale Darstellung der Vektor-Koordinaten. Im Ergebnis ist dies gleich - kann aber zu erheblicher Verwirrung führen!
- Ggf. sind Spalten und Zeilen gegeneinander zu tauschen.
3D-Transformation & 2D-Perspektive
Ein aus mehreren kaskadierten Vektoren erfaßter Roboterarm läßt sich – wie jedes andere 3D-Objekt - mit den Regeln der Winkel-Transformationen beliebig um die XYZ-Achse drehen und auch in 2D-Darstellung "perspektivisch" betrachten. Math. Zusammenfassung vgl. http://www.mttcs.org/Skripte/Pra/Material/vorlesung3.pdf.
Perspektive
- steht im Sprachgebrauch für die Darstellung 3-Dimensionaler "Tiefe" in 2-Dimensionaler Ebene - wenngleich 'Perspektive' formal lediglich eine mehrerer Darstellungsarten Planarer-Projektion ist. Sprachlich unterschieden wird gelegentlich die Parallel- und Fluchtpunkt Perspektive.
- Die Parallelprojektion arbeitet mit einer winkelabhängigen Verkürzung der in die Tiefe zeigenden Linien, die auf den hier erläuterten Winkeltransformationen basieren.
- Die Perspektive kennt zusätzliche 'Fluchtpunkte' in denen sich in der Realität parallele Linien treffen. Jedes System paralleler Linien hat einen eigenen Fluchtpunkt, dies können deutlich mehr als die 3 XYZ Koordinaten, (vgl. z.B. 'Place de l' Etoile) sein!
- Die Grenzen perspektivischer Darstellung werden deutlich, wenn wir uns Parallelen parallel zur Zeichenebene vorstellen; sie hätten 2 Fluchtpunkte – 'links und rechts' bzw. 'oben und unten'. Der Strahl aus den Fluchtpunkten führt jedoch zu einer Kreuzung in der Zeichenebene, die als "zusätzliche Ecke" erscheinen würde!
Dies ist unrealistisch, in der Schulperspektive darstellender Geometrie werden diese Parallelen daher stets 'als parallel' gezeichnet.
Aus der Fotographie kennen wir Fischaugenobjektive; die analoge Abbildung hat hier die Lösung: Der Kreuzungspunkt der "zusätzlichen Ecke" wird verrundet dargestellt. Dies entspricht – auch wenn wir nicht wie eine Fisch zu gucken gewohnt sind – der Realität! Die Flucht-Linie ist keine Linie, sondern eine Hyperbel, die sich in Richtung Fluchtpunkt den Linien asymptotisch anschmiegt, Rundung im Betrachtungszentrum.
Leistungsstarke Programme der virtuellen Bilderstellung beherrschen diese Mathematik und arbeiten außerdem mit Licht und Schatten Effekten, um die Tiefenwirkung zu verstärken. Ganz ohne Mathematik: Stephan Thiele, http://www.thiele-architekt.de/pdf/Raumsprache-A5.pdf
Transformation
- Die hier besprochene 3D-Transformation ermöglicht eine variable Parallelprojektion aus beliebiger XYZ Blickrichtung. Sie basiert rechentechnisch auf EXCEL® – ich verweise gerne auf Veröffentlichungen von Andy Pope http://www.andypope.info/charts/3drotate.htm und Klaus Kühnlein http://www.excelformeln.de/tips.html?welcher=53 , die mich zu dieser Ausarbeitung anregten - wenngleich oder gerade weil die Algorithmen zu unterschiedlichen Ergebnissen führen!
- "excelformeln" arbeitet mit dem mächtigen EXCEL® Formel-Array "MMULT"- Andy Pope zeigt für die 3D-Transformation einen ebenfalls interessanten Weg – ich möchte diese Studien hier jedoch nicht nach dem "Schavan-Guttenberg-Prinzip" wiederholen.
Zu den unterschiedlichen Transformationsergebnissen ein Experiment:
Legen wir ein Buch, am Besten zwei jeweils in Leseposition (aber geschlossen) vor uns.
- - Das Linke drehen wir zuerst um seine Y-Achse, dann um seine X-Achse,
- - das Rechte zuerst um seine X-Achse, danach um seine Y-Achse.
- Falls Sie die gleiche Position für beide Bücher erhalten, haben Sie etwas falsch gemacht!
- Bei einem Roboter-Arm können Sie das Phänomen nicht beobachten, hier ist es egal, ob Sie den Arm erst nach hinten und dann nach oben oder umgekehrt bewegen.
- - Der Grund liegt darin, daß der Roboter sein Koordinatensystem gewissermaßen mit bewegt. Bei unserem Buch-Experiment lag das Koordinatensystem hingegen starr.
- Und wenn Sie beim Buch-Experiment in beiden Fällen dasselbe Endresultat erhielten, hatten Sie eine der beiden Achsen (unbewußt) gegen die Z-Achse getauscht!
Verdrehte Koordinatenwelt
Eigentlich ist alles ganz logisch: Liegt vor uns ein Stück Papier auf dem Schreibtisch oder steht der Monitor mit senkrechtem Bildschirm vor uns, so zeigt per Definition im 2D-System die Y-Achse nach oben, die X-Achse nach rechts. Wird eine dritte Dimension hinzugefügt, so liegt sie vor bzw. hinter der Zeichenebene; die Z-Achse zeigt also aus der Zeichenebene hinaus in den Raum.
Irgendwann kamen die Menschen auf die Idee, Bildschirm bzw. Papier zu drehen – aber die körperliche Position des Betrachters bei zu behalten: Das Schicksal nahm seinen Lauf:
- Bei beiden Systemen, dem 2D- und dem 3D-System zeigt die Positive X-Achse nach rechts (auch "Breite" genannt).
- Erweitert man das 2D-System (Y-Achse nach oben, auch "Höhe" genannt) um die dritte Dimension, die Z-Achse, so zeigt diese zunächst "unsichtbar" auf den Betrachter. Dreht man dieses System um die X-Achse, so wandert die Y-Achse nach hinten, die Z-Achse nach oben. Die Z-Achse übernimmt den Namen der Y-Achse (Höhe), die Y-Achse heißt jetzt Länge – und zeigt mit positivem Wert nach hinten!
- Einige 3D-Darstellungen bevorzugen eine weitere Drehung um die nun senkrechte Z-Achse: Im Ergebnis zeigt dann die Y-Achse nach rechts und die X-Achse nach vorn.
- Unabhängig hiervon bleibt zumindest die Koordinatenbezeichnung "X/Y/Z" unverändert!
Ich habe mich entschlossen, dieses Definitions-Chaos möglichst zu umgehen und verwende die Definition des klassischen Weltkoordinatensystems: Y-Achse nach oben!
Links- & rechtshändige Koordinaten
Eine schier unerschöpfliche Vielzahl von Koordinatensystemen kennt die Welt, vgl.: https://de.wikipedia.org/wiki/Koordinatensystem. Dominierende Bedeutung in der Robotic hat das kartesische System – und hiervon gibt es 2, das rechts- und das linkshändige!
Grundsätzlich gilt (unabhängig davon, wie die Achsen benannt sind):
- Rechts- bzw. linkshändige Koordinatensysteme sind spiegelbildlich und nicht durch Drehung ineinander zu überführen, jedoch:
- Transformationsmatrizen ermöglichen eine Skalierung (Multiplikation).
- Bei unterschiedlicher Skalierung je Achse führt dies in eine Scherung (Verzerrung).
- Eine negative Skalierung führt ergänzend zu einer Spiegelung der betreffenden Achse.
Unter 'Vektortransformation' hatten wir die Rotationsmatritzen XYZ besprochen. Zur Erinnerung: Wird die betreffende "Eins" zu "-1" negiert, so wird die Achse gespiegelt. - Simpler Vorzeichenwechsel ermöglicht also die System-Umschaltung "links / rechts"!
Spiegelung ist nicht durch Drehung erreichbar, trotzdem erscheit dies mitunter so!?
- Bei einem 3D-Drahtmodel ist es mitunter schwierig zu entscheiden ob man es von 'oben-links' oder 'unten-rechts' sieht; - d.h. betrachten will! Das Seh-Ergebnis ist eine Frage des mentalen Bewußtseins.
- Das Gehirn gaukelt einem mitunter sogar vor, der mathematische Drehsinn (positiv/negativ) habe sich geändert, da das, was man vorne wähnt, nun auf einmal hinten erscheint. Dieses Wahrnehmungsphänomen wird erklärbar, weil jede Projektion eines realen Drahtmodells auf (mindestens) 2 unabhängige Raumorientierungen rückführbar ist. Anders ausgedrückt: Eine von oben gesehen vorne liegende Ecke ist nach 3D-Transformation in die 2D Projektions-Ebene zu einer von unten gesehen hinten liegenden kongruent!
- Die Visualisierung des Baukastens kennzeichnet daher als Orientierungshilfe die Ecke des 1. Oktanten mit einem Kreis, der bei Würfel Drehung betrachtungskonform mit wandert. Im 'Kochbuch des User-Manuals' finden Sie unter Perspektive & 2D-Projektion eine Experimental-Studie hierzu.
End-Effektor & Tool Center Point (TCP)
Der End-Effektor bezeichnet die Hard-Ware, der Tool Center Point dessen "Arbeitspunkt"; beide werden gemeinsam "Bahn konform" vom Robotersystem im R3 Vektorraum bewegt.
- Der TCP kann am Ende des End-Effektors liegen (Bohrer); weiter außerhalb (Laser) oder auch völlig abweichend zum "Werkzeug-Eingriffspunkt":
- - Bei einem Greifer, der "Roboterhand" liegt dessen Kraftlinien-Schnittpunkt im Werkstück!
- Eine Hardware spezifische Definition "was wie bewegt werden soll" ist Voraussetzung "Bahn konformer" Kinematik!
SCARA-Roboter
Ebenfalls unter http://www.excelformeln.de/tips.html?welcher=93 findet sich ein 2D-Roboterarm, der sich eindrucksvoll in der Ebene bewegen läßt und im Ansatz einen SCARA-Roboter simuliert. SCARA steht für: Selective Compliant Articulated Robot for Assembly. Selektiv läßt sich als "ausgewählt" in der Bedeutung von "eingeschränkt" übersetzen.
- Der SCARA bewegt sich in einer 2D-Ebene – wenngleich mehrere dieser Ebenen geschichtet sind, um die Arme "untereinander" an sich selbst vorbeiführen zu können.
- Senkrecht zu diesen plan-parallelen Bewegungs-Ebenen übernimmt am Ende der kinematischen Kette eine (meist drehbare) Hub-Achse die "TCP / End-Effektor"-Funktion.
Die SCARA Bauart ermöglicht zwar nur eingeschränkte Bewegungsmöglichkeiten ist jedoch für Anwendungen optimal, deren Zielpunkte in plan-parallelen Ebenen liegen und parallel zur (meist senkrechten) Fußpunktachse anfahrbar sind. Die Konstruktion ist kostengünstig. Die eingeschränkten kinematischen Möglichkeiten führen andererseits zu einer Vielzahl aufgabenorientierter Spezialkonstruktionen, was dem Gedanken eines "Universal-Roboters" widerspricht. Unter kinematischen Gesichtspunkten sind die Bewegungsmöglichkeiten des SCARA eine Untergruppe des "Universal" Gelenkarm-Roboters.
Gelenkarm-Roboter
Der Gelenkarm- oder Knickarm-Roboter bewegt (im Gegensatz zum SCARA) die Arbeitsachse frei im 3D-Raum, also unter beliebigem Winkel. Um ein Objekt im 3D-Raum greifen / bearbeiten zu können werden mehrerer Freiheitsgrade = Drehachsen erforderlich:
Die "Roboterhand" wird mit dem "Roboterarm" positioniert.
- Um die Hand gegenüber dem Objekt zu positionieren werden 3 Achsen (XYZ),
- um das Objekt greifen / bearbeiten zu können, weitere 3 Achsen (UVW) erforderlich,
- dies entspricht 6 Freiheitsgraden, oftmals mit "f", (im amerikanischen Sprachgebrauch mit "DOF" - degree of freedom) bezeichnet.
- Mit diesen 2 mal 3 Freiheitsgraden kann jeder beliebige Punkt im Arbeitsbereich des Roboters positioniert (XYZ) und das Werkzeug unter definiertem Winkel zum Werkstück orientiert (UVW) werden.
- Muß der Roboter um ein Hindernis herumgreifen, so werden weitere Freiheitsgrade / Drehachsen erforderlich. Optimal sind meist 5-Arm und 3-Hand Freiheitsgrade.
Die "Roboterhand" eines Gelenkarm-Roboter rotiert im einfachsten Fall um eine Roboterarm-Achse, bei höherem Freiheitsgrad ("Ellenbogen") wird die "Roboterhand" bereits von 2 bzw. 3 Drehachsen positioniert; diese bewegen sich gegenüber dem Koordinatensystem frei im Raum.
Freie Rotation
Nochmals: Die Roboterachsen bewegen sich gegenüber dem Koordinatensystem frei im Raum.
Unsere Transformationsmatrizen kennen jedoch nur Rotation um die X-, Y- oder Z-Koordinate! Für den Rechenalgorithmus bedeutet dies,
- daß eine frei im Raum stehende Dreh-Achse zunächst in den Koordinaten Nullpunkt verschoben und danach um die Winkelkomponenten zweier Koordinaten auf die verbleibende Koordinatenachse (welche ist beliebig) transferiert werden muß.
- Die transferierte Dreh-Achse wird entsprechend dem gewünschten Drehwinkel um die Koordinaten-Achse gedreht,
- die gedrehte Achse auf ihren ursprünglichen Start-Vektor zurück transferiert - und mit ihr sämtliche in der seriellen Kaskadierung folgenden Drehgelenke.
Wir erinnern das "Buchexperiment"; nach der Drehung liegt beim Linken der Rücken "unten", beim Rechten "vorn" (oder - je nach Drehrichtung - "hinten"). Dieses Phänomen macht jede Menge Ärger:
Hier die vierte wichtige Erkenntnis:
- Die Transformationsmatrizen müssen für eine Rückdrehungen in exakt umgekehrter Reihenfolge durchlaufen werden. Nach jeder Transformation ändern sich alle Winkelkomponenten.
Hieraus folgt:
Die fünfte wichtige Erkenntnis:
- Nach Transformation um eine (beliebige) Achse müssen die (neuen) Transformationswinkel der verbleibenden Achsen jeweils erneut berechnet werden, denn:
- Die aus den Vektorkoordinaten (vorab) errechneten Winkel sind nicht die Transformationswinkel, um Roboter-Achsen auf die Koordinatenachse zu transferieren.
"Step by Step" sind dies je Achse 7 Transformationen bzw. 7 x (4³ Einzelmultiplikationen + 16 Additionen) zuzüglich der in serieller Kaskade folgenden Gelenke. Eine Drehung um die Basisachse erfordert also (bei einem Freiheitsgrad von 8) ca. 4.500 Einzelrechnungen! Die 7 Winkeltransformationen lassen sich auf 6 reduzieren, nicht alle Matrizen müssen homogene Koordinaten aufweisen, sodaß sich die Rechenschritte bei Erhalt der klassischen Rechenstruktur um ca. 40% reduzieren lassen.
Transponierte Matrix
Werden die Einzelelemente einer Matrix an ihrer Hauptdiagonalen (oben links nach unten rechts) gespiegelt - formal also Spalten und Zeilen getauscht - so entsteht eine Matrix, die das (vorherige) Transformationsergebnis in seine Ausgangswerte zurückrechnet. Werden die bereits errechneten Elemente an gespiegelter Position genutzt so reduziert sich der Rechenaufwand.
- Vereinfachte Betrachtungsweise für XYZ-Rotationsmatrizen: Sin-Werte und Homogene Koordinaten invertieren das Vorzeichen, alle anderen Werte bleiben gleich.
Die "Step by Step" Transformationen nutzt dies meist für die Rückdrehung.
R3 Spezial-Matrix
Mathematiker bezeichnen den 3D-Raum auch als R3 Vektorraum. Durch geschicktes Vorab-Ausmultiplizieren des oben beschriebenen Matritzen-Algorithmus läßt sich die Zahl der Rechenschritte nochmals reduzieren: Lotte Emslander zeigt, wie's geht: http://analysis.math.uni-mannheim.de/lehre/fs09/anageo/uebung/unsichtbar/Rotationen_im_R3.pdf
Die R3 Rotations-Matrix selbst wird jedoch etwas komplex; anstelle der recht übersichtlichen "Step by Step" Struktur (und einfacher Winkel-Beziehungen) errechnet sich nun jedes der 9 Matrix-Elemente im Schnitt aus jeweils 5 Multiplikationen zuzüglich 2 Additionen. Ergänzend werden einige "Schattenrechnungen" erforderlich.
Der für den RoBo-mac Gelenk-Baukasten entwickelte EXCEL® Algorithmus optimiert aus beiden Denkschulen, er beherrscht Teleskop- und Drehgelenke in beliebiger Kombination.
In den 1950-iger Jahren wurden Algorithmen erarbeitet, um den durch Länge der Roboter-Achsen bei freier Winkelstellunge definierten Raumpunkt in das kartesische Koordinatensystem (XYZ) zu transformieren. 1955 wurden sie als Denavit-Hartenberg Convention / Transformation / Parameter propagiert https://de.wikipedia.org/wiki/Denavit-Hartenberg-Transformation , - wenngleich der Schweizer Mathematiker Leonhard Euler die Grundlagen der Winkeltransformation, vgl. https://de.wikipedia.org/wiki/Eulersche_Winkel bereits vor 300 Jahren entwickelte. Auf letztere habe ich dankbar zurückgegriffen.
Inverse Kinematik
Diese "rückwärts" Kinematik beschäftigt sich mit der Frage: "Welchen Winkelwert müssen die in kinematischer Kette liegenden Gelenke einnehmen, um einen bestimmten Raum-Punkt (kartesisch XYZ) zu erreichen" – das Ziel, der Raumpunkt ist also gegeben!
Eine Vielzahl mathematischer Denkansätze zeigt Lösungen hierzu auf. Klassisch unterschieden werden
- algebraische Methoden (Transformation und Gleichung),
- geometrische / trigonometrische Methoden (sin / cos) und
- numerische Methoden (Iteration).
und Kombinationen hieraus. – Der Königsweg wurde bisher wohl nicht gefunden; vgl. http://geometrie.uibk.ac.at/cms/datastore/husty/husty-linz.pdf , Geschichtliche Entwicklung der inversen Kinematik.
- Die Lösungsstrategie RoBo-mac's transformiert die Roboter-Achsen aus dem 3D Raum in die Ebene, sucht numerisch eine trigonometrische Lösung und prüft das Ergebnis in direkter Kinematik. Die absoluten Positionierfehler des Algorithmus liegen unter 1/10.000 mm, meist in einer Größenordnung 10-5 bis 10-6 mm.
Freiheitsgrad & kinematische Überbestimmung
Erinnern wir uns:
- Mit 2 mal 3 Freiheitsgraden kann jeder beliebige Punkt im Arbeitsbereich des Roboters positioniert (XYZ) und das Werkzeug unter definiertem Winkel zum Werkstück orientiert (UVW) werden.
- Um ein Werkzeug unter definiertem Winkel zu positionieren, werden also 6 Freiheitsgrade erforderlich. Muß der Arm um ein Hindernis herumgreifen, so wird je Freiheitsgrad mehr als eine Achse erforderlich. Kinematisch bedeutet dies eine "Überbestimmung", denn der Raumpunkt kann wahlweise durch mehrere Achsen angesteuert werden; dies macht die Mathematik deutlich komplexer!
Hilfreich ist es, Arm (XYZ) und Handgelenk (UVW) getrennt zu betrachten, da ansonsten 6 Freiheitsgrade in extreme Überbestimmung führen würden.
- Beginnen wir mit dem eigentlichen Zielpunkt, dem Werkzeug-Eingriffspunkt, er bestimmt den Übergangspunkt "Arm/Handgelenk". Dieser Bahnpunkt ist also zugleich Zielpunkt des Armes und Startpunkt des Handgelenkes – und aus der Orientierung (UVW) zu bestimmen. Vergleichbar ist er mit der aus der CNC-Technik bekannten Äquidistanten, zur Fräs-Bahnberechnung mit Radius-Korrektur.
- Liegen dieser Bahnpunkt und der eigentliche Zielpunkt im kartesischen System (XYZ) fest, so werden hieraus die Drehwinkel des Armes transformiert.
Einfacher Fall: Keine kinematische Überbestimmung.
- Per Winkeltransformation werden die 3D-Koordinaten um die Y-Achse auf Z = 0 gedreht,
- aus den nun in der Ebene liegenden XY-Koordinaten sind die Winkel zweier Roboter-Achsen trigonometrisch bestimmbar,
- Sie erhalten 2 Lösungen – beide sind richtig, eine ist vermutlich sinnvoller,
- das gewählte Zwischenergebnis wird um die Y-Achse auf den gegebenen Z-Wert zurückgedreht.
Einfache SCARA Roboter mit 2+1 = 3 Freiheitsgraden fallen in diese Kategorie.
Komplexer Fall: Kinematische Überbestimmung.
- Die 3D-Koordinaten werden auch hier um die Y-Achse auf Z = 0 gedreht,
- für die nun in der Ebene liegenden XY-Koordinaten sind (ab mehr als 2 Achsen) jedoch theoretisch unendlich viele Winkel-Kombinationen dieser Achsen möglich!
- Ist eine Winkel-Kombinationen gefunden, so wird ebenfalls um die Y-Achse auf den gegebenen Z-Wert zurückgedreht.
Bewegungsstrategie und Silhouette
Um trotz Überbestimmung aus theoretisch unendlich vielen Winkel-Kombinationen möglichst geeignete Vektorlagen der Roboterarme zu berechnen verfolgt der RoBo-mac Gelenkbaukasten mehrere, frei wählbare Bewegungsstrategien:
- Semi-Automatic präzisiert manuelle Winkel-Vorwahl "in ähnlicher Silhouette"
- Konvex: Das mittlere Arm-Element liegt oberhalb des Zielpunktes
- Konkav arbeitet vice versa zu Konvex
- Zickzack: Die Arm-Elemente bilden eine Zickzack Silhouette
- Parallel, bewegt den 'End-Effektor' parallel zu sich selbst
- Teleskop bewegt den 'End-Effektor' wie einen "Teleskop-Auszug".
Diese Bewegungsstrategien liegen in einer bzw. parallelen Bewegungsebenen. Um Zugriff im R3 zu realisieren, wird das Ebenenpaket um die (meist senkrechte) Hauptachse A/B gedreht.
Hier ein Kurzüberblick, mehr zu den Bewegungsstrategien - und wann welche sinnvoll ist - in Teil 2 Inverse Kinematik 2 – Praxis.
Semi-Automatic
- orientiert sich an der Ist-Position der Gelenke und erreicht die neue Zielposition "in ähnlicher Silhouette". Die Stützpunkt-Schrittweite beeinflußt die "Ähnlichkeit"; liegen die Stützpunkte weit auseinander, so geht die Ähnlichkeit verloren. Die Bahnen der Gelenk-punkte sind bei Hin- und Herbewegung selten kongruent.
Konvex, Konkav & Zickzack
- generieren die Bahn mit reproduzierbarer Winkelstellung der Gelenke - unabhängig von deren Ausgangs-Position. Diese Bewegungsstrategien ermitteln für alle Gelenkpunkte stets die gleiche Bahn.
Parallel
- Der 'End-Effektor' wird ebenen parallel zu sich selbst, in eigener Vektor-Orientierung bewegt, (Mathematiker nennen dies "kollinear"), und ggf. um die Hauptachse gedreht.
Teleskop
Die Begriffsverwendung bezieht sich nicht auf "FernSicht", sondern die klassische Bauart dieses Instrumentes, das in eigener Achse in der Länge veränderlich ist/war (Teleskop-Auszug etc.).
- Die Bewegungsstrategie 'teleskopisch' berechnet aus der Ist-Vektorlage des 'End-Effektors' und dem gewünschten Vektor-Hub je Bewegungsschritt Winkel-Arm Kombinationen, die den 'End-Effektor' teleskopartig in eigener Vektor-Orientierung fluchtend (auf einer Geraden) bewegen; Mathematiker nennen auch dies "kollinear".
Der mathematische Begriff "kollinear" unterscheidet nicht, ob Vektoren (wie zwei Eisenbahnschienen) parallel oder auf einer gemeinsamen Geraden "fluchtend" liegen; ich verwende ggf. den Doppel-Begriff.
Singularität
In der Mathematik beschreibt Singularität das Phänomen, daß außerhalb der Singularität geltende Algorithmen im Bereich der Singularität ihre Gültigkeit verlieren. Singularität steht hier für die "Definitionslücke einer Funktion"; einen "unbestimmten Zustand", der nicht berechnet werden kann. Relativ bekannt in diesem Focus ist die "Sprungfunktion".
Singularität in der Robotik ist Fluch und Segen zugleich: Singularität tritt auf, wenn das Gesamtsystem einen (oder mehrere) Freiheitsgrade verliert bzw. die Bewegung einer Achse durch eine andere vollständig kompensiert werden kann.
Fluch der Singularität
Innere Singularität
Singularität der Drehachsen tritt im inneren des Arbeitsraumes auf. Liegen 2 – oder mehrere Achsen "kollinear fluchtend" auf einer gemeinsamen Vektor-Linie so gibt es unendlich viele, sich gegenseitig kompensierende Drehwinkel, die auf die die TCP- / Werkzeug-Orientierung ohne Einfluß sind, umgekehrt ausgedrückt: Es ist nicht eindeutig, welche der fluchtenden Achsen gedreht werden muß, um den End-Effektor zu drehen.
Äußere Singularität
Singularität der Schwenkachsen liegt im Rand-Bereich des Arbeitsraumes. Ist der Gesamtarm voll gestreckt, so kann er nicht mehr über seinen Arbeitsbereich hinausgreifen; das ist geometrisch logisch, kann jedoch in mathematische Instabilitäten führen (Definitionslücke einer Funktion). Gleichsinniges gilt für die "Total-Faltung": 2 Achsen liegen mathematisch deckungsgleich aufeinander - für die Mechanik bedeutet dies Kollision.
- Führt die Bewegungsbahn des TCP in den Grenzbereich des Arbeitsraumes, so nehmen die Arme eine Silhouette ein, die in der Technischen Mechanik als "Kniehebel-Presse" bezeichnet wird. Kniehebel-Pressen erzeugen bei geringem Hub enorme Kräfte, die durch einen langen Hebelweg erzeugt werden:
Wird der äußere Singularitätspunkt unbeabsichtigt / unkontrolliert durchfahren, so tritt ein Bündel von Problemen auf:
- Bei "Werkzeug-Eingriff" entstehen Widerstandskräfte, die das System zerstören können.
- Um eine Roboter Bahn mit kontinuierlicher Soll-Geschwindigkeit zu durchfahren werden unterschiedlich hohe Winkelgeschwindigkeiten der Achs-Gelenke erforderlich. Nahe der Äußeren Singularität werden die Winkelgeschwindigkeiten nahezu unendlich! Um ein parasitäres Schwingen des Armes aus diesen dynamischen Kräften zu vermeiden, muß die Soll-Geschwindigkeit entsprechend herabgesetzt werden. Welche Winkelgeschwindigkeiten zulässig sind, hängt von der mechanischen Stabilität ab.
- Problematischer als die eigentliche Singularität ist die mit äußerer Singularität einhergehende "Streck- bzw. Überschlagslage": Mathematisch korrekte Algorithmen Inverser Kinematik können dazu führen, daß die Vektor-Orientierungen der Knickarm-Achsen untereinander "umschlagen": Bildlich gesprochen würde das Bein eines Menschen beim Laufen "nach vorne" einknicken.
- Wird ein Stütz-Punkt der Sollbahn in beispielsweise konvexer Silhouette positioniert der Folgepunkt hingegen in konkaver Silhouette so sind zwar beide Punkte präzise positioniert, die gefahrene Ist-Bahn weicht jedoch von der Soll-Bahn ab. Die "Streck- bzw. Überschlagslage" zwingt den TCP auf eine Ist-Bahn außerhalb der theoretischen Soll-Bahn. Die Ist-Bahn weist einen "Peak" aus. Das Gesamtsystem "erzittert" aus undefinierten Winkelgeschwindigkeiten der Schwenkachsen!
Die Probleme äußerer Singularität minimieren sich, wenn die den Singularitätspunkt einschließenden Achswinkel benachbarter Sollbahnpunkte gegen 0 gehen. Maßgebend für den Bahnfehler aus "Streck- bzw. Überschlagslage" ist der kleinere beider Winkel.
- Werte um +/- 3° sind meist unproblematisch (cos 3° = 0,99863).
- Liegen die Sollbahnpunkte rein visuell innerhalb o.g. Grenzen, werden jedoch als mech. Endlagenwerte erreicht (z.B. -179° / + 178°), so führt die Ist-Bahn über einen parasitären (nahezu) Vollkreis von 357° mit einer um 180° versetzten, negativer Stecklage!
Segen der Singularität
Wenngleich Singularität mitunter als Horror-Szenario der Robotik diffamiert ist, kann sie – bewußt eingesetzt – durchaus hilfreich sein. Ohne Einfluß auf die TCP- Position oder End-Effektor Orientierung ist die "Streck- bzw. Überschlagslage" äußerer Singularität ebenso nutzbar wie die innere Singularität fluchtender Dreh-Drehachsen:
- zu einer bewußten Um-Orientierung der Achs-Vektoren, um ein Hindernis zu umfahren
- um Drehachsen aus dem Grenzbereich ihres maximalen Drehwinkels "zurückzudrehen"
Die RoBo-mac Algorithmen beherrschen das "Problem" recht souverän, mehr hierzu im User-Manual sowie dem Video: https://www.youtube.com/watch?v=MJbAxZ3Iuio
Inverse Parallel-Kinematik
Die Algorithmen der beschriebenen Bewegungsstrategien erwarten, daß die Vektorlagen der Dreh- und Schwenkachsen "im überbestimmten Bereich" untereinander im rechten Winkel stehen. Die Schwenkachsen zwischen Schulterpunkt und Ellbogen bzw. dem Übergangspunkt "Arm/Handgelenk" bewegen sich somit in parallelen Ebenen. Die An- und Abtriebsachsen A/B bzw. G/H dürfen Drehachsen sein. Diese Parallel-Kinematik erreicht jeden beliebigen Raumpunkt (XYZ). Die absoluten Positionierfehler des RoBo-mac Algorithmus liegen unter 1/10.000 mm, meist in einer Größenordnung 10-5 bis 10-6 mm.
Inverse Schief-Kinematik
Im Gegensatz zur Parallel-Kinematik stehen die Vektoren "im überbestimmten Bereich" nicht senkrecht, sondern schiefwinklig zu einander. Die Bewegungsebenen der Achsen liegen somit ebenfalls nicht parallel, sondern stehen zu einander schief.
Bereits bei paralleler Kinematik ist die Bewegungsvielfalt aus kinematischer Überbestimmung – wenngleich nicht unendlich, so doch nahezu unermeßlich. Für die Schief-Kinematik steigt der Rechenaufwand nochmals – und führt in wahrnehmbare Rechenzeit.
Natürlich könnten die sich "in schiefen Ebenen" bewegenden Arme per Winkeltransformation in das mathematisch gut beherrschbare 2D-Modell paralleler Kinematik überführt werden; jedoch ist eine Rücktransformation wegen der sich aus der Transformation geänderten Winkel-Beziehungen nicht mehr direkt möglich (vgl. vierte und fünfte Erkenntnis). Vor diesem Hintergrund arbeitet der RoBo-mac Gelenkbaukasten ggf. mit 3D-Näherungsalgorithmen.
Näherungsalgorithmen haben stets einen Gültigkeitsbereich, der hier von Start- & Zielposition sowie der Bewegungsstrategie abhängt. Nicht jede Zielposition ist aus jeder Startposition erreichbar, ggf. muß die Bewegungsstrategie geändert bzw. die Startposition im Rahmen der Bahnoptimierung (Interaktiver Prozeß) zuvor korrigiert werden. Der Gültigkeitsbereich bildet sich aus Schnittmengen vorgenannter Parameter. Ein "Watchdog"Algorithmus überwacht, daß sich die Näherungsalgorithmen im Gültigkeitsbereich bewegen; - ggf. generiert er eine Fehlermeldung & Korrekturempfehlung.
- Der RoBo-mac Gelenkbaukasten "prüft auf Vektorlage" ob der rechenintensive Schief-Algorithmus erforderlich wird oder der schnellere Parallel-Algorithmus geeignet ist.
Linearität und Oberwelle
Die beschriebenen Bewegungsstrategien verbinden die Bahnstützpunkte. Wenngleich der Positionierfehler des RoBo-mac Algorithmus unter 1/10.000 mm liegt, so ist der Bahnverlauf zwischen den Stützpunkten mathematisch unbestimmt:
- Bestimmt wird die Bewegungs-Kinematik zwischen den Bahnstützpunkten durch die Knickarm-Mechanik: Die Rest-Welligkeit einer linearen Bahn hängt dabei (auch) von deren relativen Lage im Arbeitsbereich der Knickarme ab.
- Linearität versteht sich in diesem Zusammenhang nicht nur als Linie/Gerade, sondern als lineare Umsetzung Soll/Ist.
- So, wie bei der CNC-Fräse ein Kreis - infinitesimal betrachtet - aus einer Vielzahl von geraden Segmenten besteht, so basiert beim Knickarmroboter die Bahn auf Kreiselementen. Soll eine lineare Bewegung des TCP / Endeffektors erreicht werden, so sind hieran eine Vielzahl von überlagerten Kreisbewegungen beteiligt.
Gedankenexperiment
Wenngleich die folgende Betrachtung für jede Soll-Kurve gilt, vereinfachen wir sie im Beispiel auf eine Gerade.
- Mit einer Geraden sollen 2 gegenüberliegende Punkte auf der Peripherie des Roboter-Arbeitsbereiches verbunden werden.
- Hieran beteiligt ist in jedem Fall die Hauptdrehachse A/B; sie beschreibt einen Kreisbogen. Um diesen zu glätten wird der Knickwinkel zwischen den Armen während der Dreh-Bewegung 'A/B' zunächst reduziert und danach wieder erhöht.
- Erzeugt wird die Winkelarmbewegung über Motore. Konstant kann deren Winkelgeschwindigkeit nicht sein, denn zumindest der Knickarm Motor muß eine Hin- und Herbewegung durchführen.
- Kreisbewegungen lassen sich auf sin/cos Komponenten zurückführen. Soll die CNC-Portal-Fräse einen Kreis herstellen, so arbeitet sie nicht "wie ein Zirkel", sondern auf Basis linearer (xy-paralleler) Bewegungen mit sin/cos Geschwindigkeitsprofil. Gleichsinniges – nur umgekehrt – gilt für die Knickarme.
- Nehmen wir an, unsere Gerade läge parallel zur X-Achse, wir betrachten (Weltkoordinatensystem) aus Z-Richtung:
- Bei konstanter Drehgeschwindigkeit des Antriebs 'A/B' bewegt sich die Projektion der Drehung zunächst langsam, in der Mitte schneller, zum Ende wieder langsam – also sinus-konform. Um den Kreisbogen in eine Parallele zur X-Achse zu zwingen wird in erster Näherung eine überlagerte Sin-förmige Bewegung des Knickwinkels zwischen den Armen erforderlich. Diese Winkelbewegung kompensiert aber nicht nur wie gewünscht die Z-Komponente der Kreisbahn (Achse 'A/B'), sondern bringt eine ungewünschte Y-Komponente ein, die ebenfalls kompensiert werden muß - es wird also etwas komplexer.
- Nach Murphys Gesetz der größten Gemeinheit ist die die Knickarm-Bewegung auch noch unsymmetrisch, da die Gerade nicht durch den Roboter-Nullpunkt führen kann!
Festzuhalten ist:
- Um mit Knickarm-Kinematik eine Gerade zu erzeugen, wird nicht nur die Überlagerung mehrerer Winkelbewegungen erforderlich.
- Die Winkelgeschwindigkeit aller Knickarme unter-/ gegeneinander muß sich hierbei kontinuierlich nicht linear ändern.
Hingegen:
- Eine Bahnsteuerung verbindet 2 Stützpunkte mit einer beliebig komplexen Anzahl von Bewegungskomponenten (der RoBo-mac Multi-Achs-Controller beherrscht 8 Achsen). Die Achsen arbeiten hierzu mit individueller – aber zwischen den Stützpunkten konstanter Winkel-Geschwindigkeit. Bei achsparallelen Systemen (CNC-Portalfräse) führt dies in lineare Bewegungen, bei Knickarm-Systemen in bogenförmige. Die sich ergebenden Oberwellen sind Mechanik-spezifisch.
- Es wird also eine hohe Auflösung der Bahn mit hoher Stützpunktzahl erforderlich, um die Winkelgeschwindigkeiten "quasi kontinuierlich" gegeneinander verändern zu können
- - und so die Sollbahn "Oberwellen arm" zu realisieren.
- Dies gilt nicht nur für eine Gerade, sondern für alle Bewegungsprofile, die nicht auf die simple Kreisbahn einer Achse zurückzuführen sind.
Fazit:
- Nur eine hohe Auflösung der Soll-Bahn ermöglicht eine "Oberwellen arme" Ist-Bahn.
- - Der RoBo-Mac Bahngenerator erzeugt Bahnen mit beliebig geringer Schrittweite.
Bézier Kurven & Bahngenerator
Der Bahngenerator des Baukastens erzeugt ein Soll-Bahnprofil aus frei wählbaren Stützpunkten. Liegen die Stützpunkte (zu-) weit auseinander, beispielsweise um Pick & Place Punkte miteinander zu verbinden, so kann dies im Ergebnis in eine "wenig kontinuierliche Bewegung" des TCP führen. Die Bewegungsbahn weist Knickstellen auf, mathematisch wird dies als nicht stetige Änderung der Bahn-Krümmung beschrieben.
Bézier Kurven können Ihre Krümmung stetig ändern
Mit nur 4 "Steuerpunkten" lassen sich die erstaunlichsten Kurven formen:
- Zwei dieser Steuerpunkte liegen auf der Bahn, - nein, die Bahn entspringt und endet hier,
- die anderen Beiden liegen außerhalb der Bahn. Sie bestimmen deren "Freiform" mit ihrer stetig geänderten Krümmung. Diese beiden Steuerpunkte werden auch als "Anfasser" (engl. Handle) bezeichnet.
- Verbindet man die Anfasser mit "ihrem" Ursprungspunkt der Kurve so erhält man eine Art "Joy-Stick" – mathematisch eine Strecke, die im Einlaufpunkt zugleich Tangente der Bèzier Kurve ist. Die Kurve folgt diesen Anfassern. Sie läuft einerseits tangential ein, andererseits bestimmt die Länge der Anfasser Kurvenlänge und Kurvenkrümmung.
- Beide Anfasser haben Wirkung auf die Gesamtkurve, jedoch ist die Wirkung auf den jeweils tangential einlaufenden Kurverbereich größer.
Bézier Kurven haben also die wunderbare Eigenschaft nicht nur 2 Punkte zu verbinden:
- Liegen die Anfasser in der Vektor-Orientierung einer anderen, anschließenden Kurve oder Geraden – beispielsweise den Pick & Place Vektoren so gehen beide Kurven nahtlos ineinander über. Anders ausgedrückt:
- Zwei gegebene Bahn-Segmente, können durch Bézier-Splines "glatt" verbunden werden.
Entwickelt wurde die Mathematik, in der französischen Automobilindustrie Ende der 1950-iger, um "intuitiv schöne Kurven" zu generieren. Paradebeispiel ist der Citroen DS, den Casteljau mit einer anderen, jedoch ergebnisgleichen Mathematik entwickelte. Hintergrund Know-how zu Bézier und Casteljau unter: Bezier, Hermite & Spline Interpolation. Hier finden Sie auch die Spline-Theorie zu anderen Kurven sowie eine Studie mit dem Excel-Quellcode zu Bézier und Hermite, - letztere ist für unsere Aufgabe völlig ungeeignet!
Bézier Kurven laufen hoch präzise in ihren eigenen Tangentenpunkt ein; trotzdem ist die eigentliche Kurve, wenngleich exakt reproduzierbar manuell nur schwer beherrschbar. Allein die Kombination aus unterschiedlichen Anfasser-Längen führt in eine unendliche Kurvenvielfalt.
- Wird die Anfasser-Länge gleich '0', so wird auch die tangentiale Einlauflänge der Kurve gleich '0', die Kurve knickt ab.
- Werden die Anfasser "länger", so wird dies auch die Kurve. Je nach Winkellage der Anfasser kann sie sich vom "Hufeisen" über ein spitzwinkliges Dreieck zur "Schleife" wandeln.
- Sie wird jedoch nie über die von den 4 Steuerpunkten begrenzte Fläche hinauskragen, - das macht sie so sympathisch!
Der RoBo-Mac Bezier Generator errechnet aus den zu verbindenden Bahnsegmenten zunächst trigonometrisch die Winkellage der Tangenten. Aus Tangenten sowie dem Abstand der Bahn-Segmente bestimmt er "geeignete" Anfasser-Längen. Diese Zusammenhänge sind nicht linear, ich habe sie in o.g. Studie mit dem Excel-Quellcode offengelegt.
- Mathematisch betrachtet lassen sich mit Bézier lediglich Ovale, jedoch keine "echten" Kreise und Ellipsen erzeugen. Die Abweichungsfehler sind abhängig vom Öffnungswinkel der Tangenten. Für Winkel unter 90° liegen sie im 1/10 Promille-Bereich, für einen Halbkreis hingegen im Prozent-Bereich. Aus 3 cascadierten Bézier-Splines (s.u.) läßt sich bereits ein nahezu exakter Vollkreis formen (Radius Standardabweichung < 0,6 Promille).
- Mit dieser Einschränkung lassen sich tangential einlaufende Kreis- bzw. Ellipsen-ähnliche Segmente und natürlich Parabeln in beliebiger 3D-Lage gut realisieren.
3D-Bézier
Die klassische Bézier Kurve liegt 2 dimensional in der Ebene. Es liegt nun nahe, die im 3D Raum liegenden Tangenten der zu verbindenden Bahnsegmente per Winkeltransformation in die Ebene zu drehen, die Kurve zu berechnen und das Ergebnis zurück zutransferieren. Mit der Tangente eines Bahnsegments ist dies gewiß möglich. Das andere wird realistisch betrachtet jedoch wohl kaum in dieser Ebene liegen. Wir brauchen also eine Lösung die allgemeingültig beliebige Vektororientierungen im 3D Raum verbindet:
- Projiziert man die Tangenten der zu verbindenden Bahnsegmente in die Ebenen des XYZ Koordinatensystems, so erhält man 3 Vektorpaare und mithin 3 Bézier Kurven. Diese 3 Kurven lassen sich zu einer gemeinsamen überlagern, die einen "glatten" Übergang in die Vektoren der zu verbindenden Bahnsegmente bietet. Die Tangenten dieser Bahnsegmente können hierbei weitestgehend beliebig im 3D Raum orientiert sein.
Der Bézier Bahngenerator errechnet die Tangentenorientierung aus der Raumpunkt Differenz der beiden jeweils letzten Stützpunkte am Ende/Anfang der zu verbindenden Segmente. Wenngleich der Algorithmus die Problematik "Division durch 0" beherrscht, sollten mindestens 2 von 3 Differenzwerten (X/Y/Z) den Betrag von 'einigen Zehntel' aufweisen. Werden 2 Differenzwerte "0" so kann dies in sehr unerwartete Kurven führen.
Bézier "Wunschbahn"
Bézier Kurven laufen hoch präzise in ihren eigenen Tangentenpunkt ein; die Kurve selber ist, wenngleich exakt reproduzierbar jedoch nur bedingt auf eine "exakte Wunschbahn" zu bringen. Muß die Bahn präzise über einen oder mehrere Raumpunkte geführt werden, so wird sie in Segmentabschnitte geteilt. Mehrere Bézier Kurven verbinden diese Raumpunkte als "Cascadierter Spline". CAD/CAE Systeme arbeiten auf dieser Technologie-Basis. Vgl. Bezier, Hermite & Spline Interpolation . Je Raumpunkt bestimmt ein Stützpunkt-Paar die Orientierung der ein- und auslaufenden Kurve. Ab 3 Raumpunkten läßt sich mit Bézier ein nahezu exakter Vollkreis, ab 4 Raumpunkten eine Ellipse oder Spirale formen, der Näherungsfehler liegt wie beim Kreis im 1/10 Promille Bereich.
Bézier-Kreise, Ellipsen & Spiralen
Steht der Roboter im Zentrum des Kreises, so ist es keine besondere Aufgabe, ihn einen Kreis beschreiben zu lassen – jede Drehmaschine arbeitet nach diesem physikalischen Prinzip! Liegen Kreise jedoch asymmetrisch zu den kinematischen Achsen, so wird es interessant:
Wir wissen inzwischen, daß die Anfasser einer Bézier-Kurve außerhalb der Kurve auf deren Tangente liegen. Im Sinne einer einfachen, intuitiven Bedienerführung liegt den Algorithmen des RoBo-mac Bézier Generators jedoch die Philosophie zugrunde, die Anfasser-Orientierung direkt aus der eigentlichen Kurve zu berechnen. Wir suchen also Punkte der Bewegungsbahn, aus denen die Orientierung der Anfasser ableitbar wird.
Wie immer die Punkte auf der Kreisbahn auch liegen: Verbindet man sie mit einer Geraden, so wird sich keine Tangente, sondern eine Sekante bilden. Theoretisch könnten an Stelle der "90° Punkte" eines Kreises 2 eng benachbarte Punkte die Sekante bestimmen – die im Grenzfall in eine Tangente übergeht. Für eine Zeichnung mag dies durchaus ausreichend sein. Soll die Bahn jedoch dynamisch durchlaufen werden, so führt dies unweigerlich in eine nahezu schlagartige Unterbrechung der durch die Stützpunktweite bestimmten Winkelgeschwindigkeit – bei einfachen Bahnsteuerungen "ruckt" der Arm!
Legt man den Stützpunkt hingegen ins Abstandsraster der übrigen Bahnpunkte, so ist dieses Dynamik-Problem eliminiert, allerdings klaffen jetzt Sekante und die zu suchende Tangente weit auseinander:
- Der Winkelfehler zwischen Sekante und gesuchter Tangente ist jedoch leicht korrigierbar: - Er beträgt = ½ Öffnungswinkel des durch die Sekante bestimmten Kreis-Segments.
- Der Winkel des so korrigierten Bézier-Kreis Segmentes reduziert sich entsprechend.
Im Ergebnis setzen sich die Stützpunkte des Kreises aus den "90° Punkten", den korrespondierenden Sekanten-Punkten und den zwischen beiden liegenden Bézier-Punkten zusammen.
Das klingt etwas komplex. In der Tat, der Rechenaufwand übersteigt den der klassischen Mathematik. Zu den oben beschriebenen Bézier-Kreis Algorithmen kommt bei Ellipsen und Spiralen weiterer Korrekturbedarf der Tangentenwinkel hinzu:
- Die "archimedische" Spirale ändert Radius und Steigung kontinuierlich mit ihrem Drehwinkel. Im Ergebnis führt dies zu einem mit zunehmender Windungszahl abnehmenden Steigungswinkel. Radius und Tangente einer Spirale stehen nie senkrecht aufeinander.
- Es gibt eine Vielzahl ausgesprochen interessanter Verfahren, Ellipsen zu erzeugen - das Internet ist voll hiervon! Eine der mathematischen Betrachtungsweisen ist die, daß sich der Radius während einer Drehung 2 mal verkürzt bzw. verlängert. Im min/max Punkt des Radius steht die Ellipsen-Tangente senkrecht zum Radius – aber nur hier!
Wenngleich mich der Gedanke faszinierte, all dies auf Bézier Basis zu generieren, habe ich mich für die klassische Mathematik entschieden.
Fazit
- Bézier ist großartig wenn Tangenten verfügbar sind; müssen Sie jedoch aus Mittelpunktslagen errechnet werden, so ist die klassische Berechnung eindeutig im Vorteil. Zu dieser Erkenntnis bin ich gelangt, als ich RoBo-mac den Weg durch das Labyrinth von Chartres gezeigt habe!
Labyrinth von Chartres
Zunächst meinen herzlichen Dank Herrn Erwin Reißmann für die Koordinaten der Wende- und Radienwechsel Punkte des Labyrinths. Aus diesen 70 Konstruktionspunkten hat der Bahngenerator in den beschriebenen Technologien zunächst die Laufbahn errechnet; in Inverser Kinematik ist hieraus die Winkelberechnung der Gelenkarme entstanden.
Als ausgewiesener Experte antiker Labyrinthe zeigt Reißmann in seinem Blog u.a. das Labyrinth von Chartres und hier die Verlegung des Ariadnefadens durch RoBo-mac. https://bloggermymaze.wordpress.com/2018/12/30/ein-roboter-zeichnet-den-ariadnefaden-im-labyrinth-von-chartres/
- Klicken Sie die Grafik für eine Fahrt durch das Labyrinth!
- Die GIF-Grafik zeigt lediglich einen Teil der Labyrinth-Fahrt, die vollständige Fahrt ist Bestandteil des Download-Demopaketes.
Bei 34 Mittelpunkten besteht die Bahnkurve des Labyrinths aus 64 unterschiedlichen Kreissegmenten und wenigen Geraden mit jeweils tangentialem Übergang. Die im Beispiel generierte Labyrinth Bahn wird mit ca. 950 Bahnpunkten beschrieben, zentrische Kreissegmente werden mit größerer Schrittweite als nicht zentrische durchlaufen (vgl. Oberwelle).
Die Labyrinthfahrt erfordert eine Drehwinkelfreiheit der Hauptachse A/B von rund 360°. Der Roboterarm steht jedoch zunächst senkrecht in 'Home-Position' (Mittelstellung 0° +/- 180°). Vor Eintritt in das Labyrinth dreht er über eine 3D-Bezierkurve in die 'Startposition Labyrinth'. Beteiligt sind die Hautachse A/B mit rund 170° Drehwinkel sowie die Gelenkarme. In 'Home-Position' zeigt der den 'End Effector' führende Arm G/H senkrecht nach oben, bei Eintritt in das Labyrinth steht er absolut senkrecht zur Bewegungsebene und zeigt nach unten. - Er hat während des Durchlaufens der Bezier-Kurve seine Orientierung von zunächst senkrecht nach oben in senkrecht nach unten gewechselt!
- Grundsätzlich wird es nur möglich, Positionierung und Orientierung im 3D Raum ohne Einschränkung frei zu wählen, wenn mindestens 2 x 3 Freiheitsgrade (Arm: X/Y/Z) und (Handgelenk: U/V/W) mechanisch vorhanden und ohne gegenseitige Beeinflussung ansteuerbar sind.
- Wird lediglich eine senkrechte Ausrichtung des Endeffektors erforderlich, so bietet RoBo-mac für Roboter "ohne Handgelenk" durch entsprechende Gegendrehung der Achsen mit den Bewegungsstrategien 6 und 7 eine einfache Lösung (näheres hierzu im 'Kochbuch Inverse Kinematik').
Mit einem Bewegungsfehler im 1/10 Promille Bereich wird diese senkrechte Orientierung während des gesamten Labyrinth Durchlaufs beibehalten. Gegen Ende der Fahrt weicht die Hauptachse in Portal Kinematik zurück, um dem End Effektor die kollisionsfreie Anfahrt der Null-Koordinate zu ermöglichen.
Kollision
Inverse Kinematik und Überbestimmung bedeuten auch, daß der Roboterarm mit sich selbst oder seiner "Umwelt" kollidieren kann. Theoretisch kann jede beliebige Stelle jedes einzelnen Roboter-Arms kollidieren; die Anzahl der Kollisionspunkte ist zwar nicht unendlich aber nahezu unermeßlich.
Die präzise Kollisionsvorhersage ist ein hochkomplexes Thema, es gibt mehrere theoretische Ansätze. Grundlagen hierzu in der Diplom-Arbeit v. Dominik Henrich unter https://kluedo.ub.uni-kl.de/frontdoor/index/index/docId/1029
Für eine Vorhersage werden Roboter-Geometrie und Umwelt als mathematisches "Drahtmodell" erfaßt und "Kollisionsvektoren" gespannt. Einerseits nimmt für feine Drahtmodelle der Modellierungsaufwand Größenordnungen visueller Bilderzeugung an, andererseits die Anzahl möglicher – wenngleich ähnlicher - Kollisionsvektoren exponentiell zu. An Stelle eines feinen Drahtmodells wird daher meist nur die wesentliche Kontur mit leicht zu berechnenden Körpern (Kugel, Zylinder, Quader etc.) nachgebildet, um so den Rechenaufwand erträglich zu halten. Ein zusätzlicher "Filter-Algorithmus" selektiert vor der eigentlichen Vektoranalyse die jeweils potentiellen Kollisionspunkte.
Außerhalb des Roboter-Arbeitsbereiches besteht keine Kollisionsgefahr. Der Arbeitsbereich wird deshalb mit einer Umhausung von der Umwelt abgetrennt, die die potentiellen Kollisionspunkte auf den Zugriffsbereich des TCP minimiert. Üblicher Weise sind die Umwelt-Kollisionspunkte innerhalb des Arbeitsbereiches starr / unbewegt. Die Kollision eines Roboters mit seiner gekapselten Umwelt ist somit verhältnismäßig leicht zu vermeiden. Deutlich komplexer ist die Kollisionsprognose eines Gelenkarm-Roboters "mit sich selbst".
- Bei der Eigenkollision bewegen sich die Arme aufeinander zu; die Komplexität erhöht sich exponentiell mit Zunahme des Freiheitsgrades.
- Eigenkollision kann bei SCARA-Roboter konstruktiv vollständig ausgeschlossen werden, da sich die Arme in verschiedenen Ebenen bewegen.
RoBo-mac Kollisionsprognose
Der RoBo-mac Gelenkbaukasten fokussiert auf die Vermeidung von Eigenkollision, er kombiniert eine Filter-Analyse mit der Möglichkeit visueller Kontrolle aus beliebiger Perspektive. Der Algorithmus spannt virtuell um jede Armachse einen mit einer Halb-Kugel abgeschlossenen Zylinder und prüft die anzufahrende Zielkoordinate auf Durchdringung "verbotener Räume".
- Auskragungen im Antriebsbereich werden nicht getrennt modelliert, sondern sollten durch Wahl eines geeigneten Zylinder-Radius von diesem abgedeckt werden.
- Die Grenzen des Algorithmus liegen darin, daß nicht die eigentliche Bahnbewegung zwischen den Stützpunkten, sondern lediglich der Zielpunkt überwacht wird. Theoretisch kann eine zu große Schrittweite der Stützpunkte so dazu führen, daß ein Kollisionspunkt übersprungen und nicht detektieret wird.
Von der Theorie zur Praxis
Hier der Link zum Praxis orientierten Teil 2. Inverse Kinematik 2 – Praxis. Besprochen werden u.a.
- die Kinematik auf Portal verfahrbarer Knickarm-Roboter,
- ein 3D-Bahngenerator und kinematische Strategien, trotz Überbestimmung aus der "Sollbahn" geeignete Winkel der Knickarme zu errechnen.
Weblinks
- Den Mathematischen 3D Gelenk-Baukasten für Rotations- & Teleskope-Achsen erhalten Sie im Download als kostenloses Test-Paket direkt von meiner Website: http://www.cnc-mac.de/html/download.html.
- Was der Baukasten kann, zeigt das Video "Inverse-Kinematik_Robotic-Simulation"; es besteht aus mehr als 3.000 Frames - das sprengt alles; daher in YouTube: https://www.youtube.com/watch?v=MJbAxZ3Iuio
- Bevor ich mich auf Kinematik und die Mathematik der Spline & Bezier-Welt vgl.: Bezier, Hermite & Spline Interpolation & Bézier und die Kettenlinie stürzte, habe ich mich mit Antriebstechnik beschäftigt. Hier im RoboterNetz finden Sie
- Stepmotore und deren Ansteuerung
- Servomotore und deren Ansteuerung (1) sowie Servomotore und deren Ansteuerung (2)
Mehr dazu unter
All dies muß getestet werden, ich habe hierzu OKTAVIAX, den Acht-Achser entwickelt; unter
http://www.youtube.com/watch?v=TT344LsOnuY
macht er ein Tänzchen (Bitte Lautsprecher einschalten).
NLB