Frank (Diskussion | Beiträge) (→Hexapods in der Kurve) |
(→Spinnenbeine) |
||
| Zeile 3: | Zeile 3: | ||
Wenn man sich erstmal nicht damit zufriedengibt, einfach mit den Beinen irgendwie herumzurudern ("Hauptsache, es bewegt sich"), sind Beinbewegungen gar nicht so ohne. | Wenn man sich erstmal nicht damit zufriedengibt, einfach mit den Beinen irgendwie herumzurudern ("Hauptsache, es bewegt sich"), sind Beinbewegungen gar nicht so ohne. | ||
| − | Schauen wir uns mal die häufigste Variante an, das ist die echsen- oder spinnenartigen Bauformen. | + | Schauen wir uns mal die häufigste Variante an, das ist die echsen- oder spinnenartigen Bauformen. Hauptmerkmal ist, daß die Beine seitlich am Körper angebracht sind. |
====Ein Beinpaar im Querschnitt==== | ====Ein Beinpaar im Querschnitt==== | ||
| − | + | [[Bild:Podlegside.jpg]] | |
| − | + | ||
(Die Beinhaltung ist hier ganz allgemein gehalten, tatsächlich sind da große Unterschiede, je nach Bauart.) | (Die Beinhaltung ist hier ganz allgemein gehalten, tatsächlich sind da große Unterschiede, je nach Bauart.) | ||
*Z ist die vertikale Drehachse des "Schulter"-Gelenks | *Z ist die vertikale Drehachse des "Schulter"-Gelenks | ||
| − | |||
*h ist die Höhe des Körpers über dem Boden | *h ist die Höhe des Körpers über dem Boden | ||
*a ist der Oberschenkel | *a ist der Oberschenkel | ||
| + | *β der Winkel des Oberschenkels | ||
| + | *K ist das Knie | ||
*b ist der Unterschenkel | *b ist der Unterschenkel | ||
| − | *α der Winkel im Knie | + | *α der Winkel im Knie |
| − | + | *F ist der Fußpunkt | |
| − | * | + | *γ der Winkel, den der Unterschenkel mit dem Boden einnimmt |
| − | * | + | *r ist der resultierende Radius des Fußpunktes um die Schulter |
| − | + | ||
| + | ====Variante "Lynxmotion"==== | ||
| + | [[Bild:Podlynx.jpg]] | ||
| − | + | Hier ist der Oberschenkel gewissermaßen geteilt. Der vertikal bewegliche Teil davon ist sehr kurz und als Parallelogramm ausgeführt, um den Unterschenkel senkrecht halten zu können. Dieser kann aktiv nur gehoben und gesenkt werden, durch Federn hat er aber ein gewisses seitliches Spiel. | |
| − | + | Der Zweck dieser Konstruktion ist es, das Schultergelenk mit nur einem Freiheitsgrad sehr robust ausführen zu können. | |
| − | man findet die Werte aus der | + | ====Ein (linkes) Bein von oben==== |
| + | |||
| + | [[Bild:Podlegtop.jpg]] | ||
| + | |||
| + | man findet die Werte aus der seitlichen Ansicht | ||
*Z die vertikale Drehachse der Schulter (bleiben wir mal bei "Schulter") | *Z die vertikale Drehachse der Schulter (bleiben wir mal bei "Schulter") | ||
| − | *r<sup>min</sup> als kleinstmöglicher Radius | + | *r<sup>min</sup> als kleinstmöglicher Radius, den der Fußpunkt beschreiben kann (wenn der Unterschenkel maximal angezogen ist = kleines α) |
| − | *r<sup>max</sup> als größtmöglicher Radius | + | *r<sup>max</sup> als größtmöglicher Radius (= grosses α) |
| − | *& | + | *δ<sup>max</sup> das ist der größtmöglich Drehwinkel des Schultergelenks |
| − | + | ||
| − | + | schraffiert ist das Bereich, in dem sich die "Fußspitze" bewegen kann. | |
| + | |||
| + | '''s''' ist somit die größtmögliche Schrittweite (bei gerader Fortbewegung) | ||
und dann noch | und dann noch | ||
| − | *M ist der Schwerpunkt des gesamten Fahrzeuges | + | *M ist der Schwerpunkt (oder Mittelpunkt) des gesamten Fahrzeuges |
| − | * | + | *br die halbe Breite |
| − | *f der Abstand | + | *f der Abstand dieses Beines von der Querachse |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ===== | + | ===Beinbewegung=== |
| − | + | ====Geradaus==== | |
| + | Wird das Bein nun für einen Schritt von vorne nach hinten gedreht (durch Drehung des "Schulter"-Servos), würde sich die Fußspitze in einem Kreisbogen bewegen. Unterwegs würde allerdings die Fußspitze nach außen wegrutschen. Am schlimmsten daran ist der Verlust der Haftreibung, von der noch zu sprechen ist. | ||
| + | Das Bein muß also unterwegs so verkürzt werden, daß sich die Fußspitze entlang der geraden Sehne '''s''' bewegt. Und dann muß noch die Winkelgeschwindigkeit des Schultergelenks angepaßt werden, da ja auch der Radius kontinuierlich verändert wird. | ||
| + | ====In einer Kurve==== | ||
| + | Um irgendein Fahrzeug in eine Kurve nach rechts zu bringen, kann man z.B. die Räder links schneller drehen lassen. Sowas geht bei Beinen natürlich nicht. Hier muß die Schrittweite variiert werden. | ||
Und noch eine Tücke in der Kurve: Der Schreitweg '''s''' muß um den Mittelpunkt des Kurvenradius einen Bogen machen. | Und noch eine Tücke in der Kurve: Der Schreitweg '''s''' muß um den Mittelpunkt des Kurvenradius einen Bogen machen. | ||
http://www.roboternetz.de/wiki/uploads/Main/podleg2.jpg | http://www.roboternetz.de/wiki/uploads/Main/podleg2.jpg | ||
| + | ===Anordnung der Beine=== | ||
| + | ====Hexapod==== | ||
| − | + | [[Bild:Hextop1.jpg]] | |
| + | [[Bild:Hextop2.jpg]] | ||
| − | + | das sind zwei Möglichkeiten, bei einem Hexpod die Beine anzuordnen. Die linke Variante hat den Vorteil, daß beim Geradeauslauf die Bewegungen der Beine identisch sein können, allerdings den Nachteil, daß der Rumpf länger sein muß (damit sich die Beine nicht in die Quere kommen). Die rechte Bauart hat diesen Nachteil nicht, aber dafür sind die erforderlichen Schrittbewegungen komplizierter. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ===Schrittfolge=== | ||
| + | Es ist ja klar, daß wir nicht alle sechs Beine gleichzeitig bewegen können. Man braucht also eine Schrittfolge. | ||
| + | ====geradeaus 3:3==== | ||
Die folgende Methode wird gerne angewandt, weil sie recht einfach und auch rein mechanisch gemacht werden kann. Die Beine 1, 4 u. 5 bzw. 2, 3 u. 6 werden jeweils gleich angesteuert, phasenmäßig aber um 180 Grad versetzt. | Die folgende Methode wird gerne angewandt, weil sie recht einfach und auch rein mechanisch gemacht werden kann. Die Beine 1, 4 u. 5 bzw. 2, 3 u. 6 werden jeweils gleich angesteuert, phasenmäßig aber um 180 Grad versetzt. | ||
Im linken Bild sind die Beine 2, 3 u. 6 gerade ganz vorne, die anderen Beine 1, 4 u. 5 ganz hinten | Im linken Bild sind die Beine 2, 3 u. 6 gerade ganz vorne, die anderen Beine 1, 4 u. 5 ganz hinten | ||
| − | + | [[Bild:Podstp1.jpg]] | |
| − | + | [[Bild:Podstp2.jpg]] | |
Im rechten Bild sind 2, 3 u. 6 mit ihrer Bewegung fertig, sie haben das Fahrzeug fortbewegt, jetzt kehrt sich die Sache um | Im rechten Bild sind 2, 3 u. 6 mit ihrer Bewegung fertig, sie haben das Fahrzeug fortbewegt, jetzt kehrt sich die Sache um | ||
| − | + | '''Schwerpunkt ?''' | |
| + | |||
Unterstützt wird das ganze Gerät immer an den Fußpunkten der Beine. Verbindet man diese jeweils drei Punkte, ergeben sich zwei Dreiecke, die in den beiden Zeichnungen strichliert angedeutet sind. Teilweise überlappen sie sich, das ist das Bereich, wo sich der Schwerpunkt des ganzen Fahrzeuges befinden darf | Unterstützt wird das ganze Gerät immer an den Fußpunkten der Beine. Verbindet man diese jeweils drei Punkte, ergeben sich zwei Dreiecke, die in den beiden Zeichnungen strichliert angedeutet sind. Teilweise überlappen sie sich, das ist das Bereich, wo sich der Schwerpunkt des ganzen Fahrzeuges befinden darf | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Und man sieht, daß diese Fläche bemerkenswert klein ist. | Und man sieht, daß diese Fläche bemerkenswert klein ist. | ||
| − | + | ===Hexapods in der Kurve=== | |
Nochmals das Bild von oben | Nochmals das Bild von oben | ||
| − | + | [[Bild:Hextop1.jpg]] | |
Die effektiven Beinwege '''s''' können auch wie die Räder von einem sechsrädrigen Fahrzeug verstanden werden. | Die effektiven Beinwege '''s''' können auch wie die Räder von einem sechsrädrigen Fahrzeug verstanden werden. | ||
Version vom 21. November 2005, 12:41 Uhr
Inhaltsverzeichnis
Spinnenbeine
Wenn man sich erstmal nicht damit zufriedengibt, einfach mit den Beinen irgendwie herumzurudern ("Hauptsache, es bewegt sich"), sind Beinbewegungen gar nicht so ohne.
Schauen wir uns mal die häufigste Variante an, das ist die echsen- oder spinnenartigen Bauformen. Hauptmerkmal ist, daß die Beine seitlich am Körper angebracht sind.
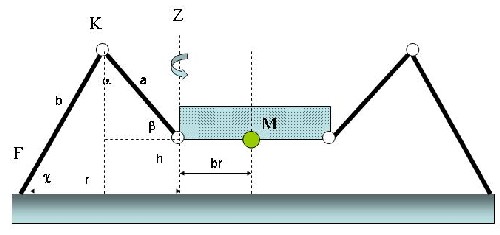
Ein Beinpaar im Querschnitt
(Die Beinhaltung ist hier ganz allgemein gehalten, tatsächlich sind da große Unterschiede, je nach Bauart.)
- Z ist die vertikale Drehachse des "Schulter"-Gelenks
- h ist die Höhe des Körpers über dem Boden
- a ist der Oberschenkel
- β der Winkel des Oberschenkels
- K ist das Knie
- b ist der Unterschenkel
- α der Winkel im Knie
- F ist der Fußpunkt
- γ der Winkel, den der Unterschenkel mit dem Boden einnimmt
- r ist der resultierende Radius des Fußpunktes um die Schulter
Variante "Lynxmotion"
Hier ist der Oberschenkel gewissermaßen geteilt. Der vertikal bewegliche Teil davon ist sehr kurz und als Parallelogramm ausgeführt, um den Unterschenkel senkrecht halten zu können. Dieser kann aktiv nur gehoben und gesenkt werden, durch Federn hat er aber ein gewisses seitliches Spiel.
Der Zweck dieser Konstruktion ist es, das Schultergelenk mit nur einem Freiheitsgrad sehr robust ausführen zu können.
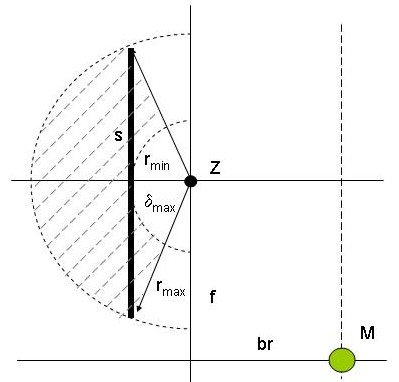
Ein (linkes) Bein von oben
man findet die Werte aus der seitlichen Ansicht
- Z die vertikale Drehachse der Schulter (bleiben wir mal bei "Schulter")
- rmin als kleinstmöglicher Radius, den der Fußpunkt beschreiben kann (wenn der Unterschenkel maximal angezogen ist = kleines α)
- rmax als größtmöglicher Radius (= grosses α)
- δmax das ist der größtmöglich Drehwinkel des Schultergelenks
schraffiert ist das Bereich, in dem sich die "Fußspitze" bewegen kann.
s ist somit die größtmögliche Schrittweite (bei gerader Fortbewegung)
und dann noch
- M ist der Schwerpunkt (oder Mittelpunkt) des gesamten Fahrzeuges
- br die halbe Breite
- f der Abstand dieses Beines von der Querachse
Beinbewegung
Geradaus
Wird das Bein nun für einen Schritt von vorne nach hinten gedreht (durch Drehung des "Schulter"-Servos), würde sich die Fußspitze in einem Kreisbogen bewegen. Unterwegs würde allerdings die Fußspitze nach außen wegrutschen. Am schlimmsten daran ist der Verlust der Haftreibung, von der noch zu sprechen ist.
Das Bein muß also unterwegs so verkürzt werden, daß sich die Fußspitze entlang der geraden Sehne s bewegt. Und dann muß noch die Winkelgeschwindigkeit des Schultergelenks angepaßt werden, da ja auch der Radius kontinuierlich verändert wird.
In einer Kurve
Um irgendein Fahrzeug in eine Kurve nach rechts zu bringen, kann man z.B. die Räder links schneller drehen lassen. Sowas geht bei Beinen natürlich nicht. Hier muß die Schrittweite variiert werden. Und noch eine Tücke in der Kurve: Der Schreitweg s muß um den Mittelpunkt des Kurvenradius einen Bogen machen.
http://www.roboternetz.de/wiki/uploads/Main/podleg2.jpg
Anordnung der Beine
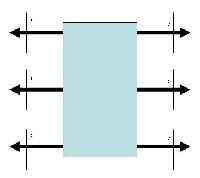
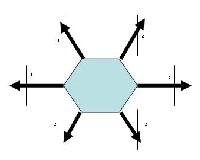
Hexapod
das sind zwei Möglichkeiten, bei einem Hexpod die Beine anzuordnen. Die linke Variante hat den Vorteil, daß beim Geradeauslauf die Bewegungen der Beine identisch sein können, allerdings den Nachteil, daß der Rumpf länger sein muß (damit sich die Beine nicht in die Quere kommen). Die rechte Bauart hat diesen Nachteil nicht, aber dafür sind die erforderlichen Schrittbewegungen komplizierter.
Schrittfolge
Es ist ja klar, daß wir nicht alle sechs Beine gleichzeitig bewegen können. Man braucht also eine Schrittfolge.
geradeaus 3:3
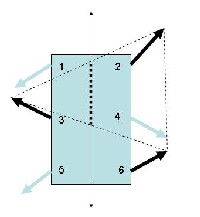
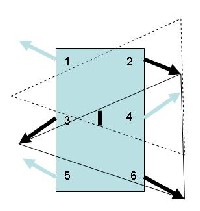
Die folgende Methode wird gerne angewandt, weil sie recht einfach und auch rein mechanisch gemacht werden kann. Die Beine 1, 4 u. 5 bzw. 2, 3 u. 6 werden jeweils gleich angesteuert, phasenmäßig aber um 180 Grad versetzt.
Im linken Bild sind die Beine 2, 3 u. 6 gerade ganz vorne, die anderen Beine 1, 4 u. 5 ganz hinten
Im rechten Bild sind 2, 3 u. 6 mit ihrer Bewegung fertig, sie haben das Fahrzeug fortbewegt, jetzt kehrt sich die Sache um
Schwerpunkt ?
Unterstützt wird das ganze Gerät immer an den Fußpunkten der Beine. Verbindet man diese jeweils drei Punkte, ergeben sich zwei Dreiecke, die in den beiden Zeichnungen strichliert angedeutet sind. Teilweise überlappen sie sich, das ist das Bereich, wo sich der Schwerpunkt des ganzen Fahrzeuges befinden darf
Und man sieht, daß diese Fläche bemerkenswert klein ist.
Hexapods in der Kurve
Nochmals das Bild von oben
Die effektiven Beinwege s können auch wie die Räder von einem sechsrädrigen Fahrzeug verstanden werden.
Wenn wir nun eine Kurve beschreiben wollen, verkürzen wir die Wege s auf einer Seite, dadurch ergibt sich ein Drehpunkt P