Spinnenbeine (Hexapods): Unterschied zwischen den Versionen

Version vom 18. Februar 2007, 21:31 Uhr

Spinnenbeine, Hexapods, Quadropods und Polypods

Wenn man sich erstmal nicht damit zufriedengibt, einfach mit den Beinen irgendwie herumzurudern ("Hauptsache, es bewegt sich"), sind Beinbewegungen gar nicht so ohne.

Schauen wir uns mal die häufigste Variante an, das sind die echsen- oder spinnenartigen Bauformen. Hauptmerkmal ist, dass die Beine seitlich am Körper angebracht sind.

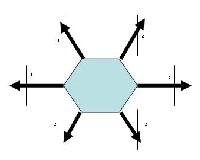
Dabei können folgende Anordnungen und Beine unterschieden werden: Die auf dem Bild gezeigte anordnung von 3 Beinen links so wie rechts ist die gängigste für Hexabots. Alternativ können die Beine auch in einem Sechseck angeordnet werden (siehe auch Bild weiter unten). Diese Anordnung hat den Vorteil, dass sie etwas wendiger ist, dies erkauft man sich durch eine etwas komplizierte Programmierung. Denn die Beinstellungen sind hier aufwendiger.

Roboter mit nur 4 Beinen werden gemeinhin als Quadropods bezeichnet. Roboter mit mehr als 6 Beinen werden als Polypod bezeichnet.

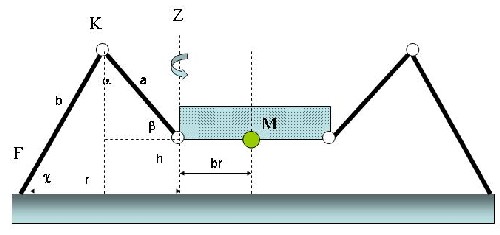
Ein Beinpaar im Querschnitt

Das hier dargestellte Bein hat 3 Gelenke (jedoch sind nur 2 sichtbar). Einmal ein Gelenk an der Schulter und eines am Knie, das nicht sichtbare ist in der ansicht von Oben dafür verantwortlich das Bein vor und zurück zu bewegen. Somit hat diese Bein 3 Freiheitsgrade (1x Knie, 1x Schulter (auf und ab) und 1x Schulter (vor zurück) dies wird oft auch als 3DOF (Degree of Freedom) bezeichnet.

(Die Beinhaltung ist hier ganz allgemein gehalten, tatsächlich sind da große Unterschiede, je nach Bauart.)

Z ist die vertikale Drehachse des "Schulter"-Gelenks
h ist die Höhe des Körpers über dem Boden
a ist der Oberschenkel
β der Winkel des Oberschenkels
K ist das Knie
b ist der Unterschenkel
α der Winkel im Knie
F ist der Fußpunkt
γ der Winkel, den der Unterschenkel mit dem Boden einnimmt
r ist der resultierende Radius des Fußpunktes um die Schulter
M der Schwerpunkt unseres Roboters
br der Abstand des Schwerpunkts bis zur Schulter

Variante "Lynxmotion"

Hier ist der Oberschenkel gewissermaßen geteilt. Der vertikal bewegliche Teil davon ist sehr kurz und als Parallelogramm ausgeführt, um den Unterschenkel senkrecht halten zu können. Dieser kann aktiv nur gehoben und gesenkt werden, durch Federn hat er aber ein gewisses seitliches Spiel.

Der Zweck dieser Konstruktion ist es, das Schultergelenk mit nur einem Freiheitsgrad sehr robust ausführen zu können. Diese Variante der Beine hat also insgesammt nur 2 Freiheitsgrade (Schulter und heben, senken) und wird oft auch als DOF2 bezeichnet.

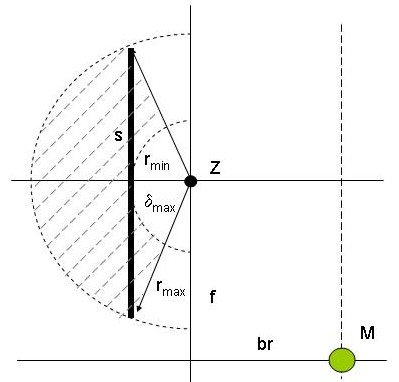
Ein (linkes) Bein von oben

man findet die Werte aus der seitlichen Ansicht

Z die vertikale Drehachse der Schulter (bleiben wir mal bei "Schulter")
r^min als kleinstmöglicher Radius, den der Fußpunkt beschreiben kann (wenn der Unterschenkel maximal angezogen ist = kleines α)
r^max als größtmöglicher Radius (= großes α)
δ^max das ist der größtmögliche Drehwinkel des Schultergelenks

schraffiert ist der Bereich, in dem sich die "Fußspitze" bewegen kann.

s ist somit die größtmögliche Schrittweite (bei gerader Fortbewegung)

und dann noch

M ist der Schwerpunkt (oder Mittelpunkt) des gesamten Fahrzeuges
br die halbe Breite
f der Abstand dieses Beines von der Querachse

Beinbewegung

Geradeaus

Wird das Bein nun für einen Schritt von vorne nach hinten gedreht (durch Drehung des "Schulter"-Servos), würde sich die Fußspitze in einem Kreisbogen bewegen. Unterwegs würde allerdings die Fußspitze nach außen wegrutschen. Am schlimmsten daran ist der Verlust der Haftreibung, von der noch zu sprechen ist.

Das Bein muß also unterwegs so verkürzt werden, daß sich die Fußspitze entlang der geraden Sehne s bewegt. Und dann muss noch die Winkelgeschwindigkeit des Schultergelenks angepasst werden, da ja auch der Radius kontinuierlich verändert wird.

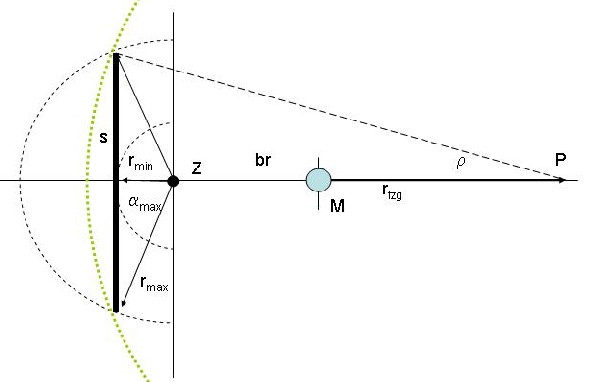
In einer Kurve

Um irgendein Fahrzeug in eine Kurve nach rechts zu bringen, kann man z.B. die Räder links schneller drehen lassen. Sowas geht bei Beinen natürlich nicht. Hier muß die Schrittweite variiert werden. Und noch eine Tücke in der Kurve: Der Schreitweg s muss um den Kurvenradius-Mittelpunkt einen Bogen machen.

P Kurven-Mittelpunkt
M Fahrzeugmittelpunkt
r_fzgRadius des Fahrzeuges um P

Anordnung der Beine

Hexapods

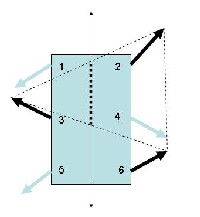
das sind zwei Möglichkeiten, bei einem Hexpod die Beine anzuordnen. Die linke Variante hat den Vorteil, dass beim Geradeauslauf die Bewegungen der Beine identisch sein können, allerdings den Nachteil, dass der Rumpf länger sein muss (damit sich die Beine nicht in die Quere kommen). Die rechte Bauart hat diesen Nachteil nicht, aber dafür sind die erforderlichen Schrittbewegungen komplizierter.

Schrittfolge

Es ist ja klar, daß wir nicht alle sechs Beine gleichzeitig bewegen können. Man braucht also eine Schrittfolge. Hier können mehrere Varianten unterschieden werden. Da ein Spinnenroboter 6 Beine hat und zum stehen 3 Stück (ein Dreieck bildend) ausreichen gibt es: 3:3. Wir können aber auch nur 2 Beine bewegen und 4 auf dem Boden stehen lassen also 2:4 oder alternativ nur ein Bein bewegen und mit den restlichen 5 auf dem Boden stehen, also 5:1. In Kurven ist das ganze noch etwas komplizierter daher beschäftigen wir uns als erstes mit:

geradeaus 3:3

Die folgende Methode wird gerne angewandt, weil sie recht einfach und auch rein mechanisch gemacht werden kann, allerdings ist die Belastung für die Servos bei dieser Variante am grössten, denn nur 3 Beine teilen sich das gesamte Gewicht des Roboters. Die Beine 1, 4 u. 5 bzw. 2, 3 u. 6 werden jeweils gleich angesteuert, phasenmäßig aber um 180 Grad versetzt.

Im linken Bild sind die Beine 2, 3 u. 6 gerade ganz vorne, die anderen Beine 1, 4 u. 5 ganz hinten

Im rechten Bild sind 2, 3 u. 6 mit ihrer Bewegung fertig, sie haben das Fahrzeug fortbewegt, jetzt kehrt sich die Sache um

Schwerpunkt ?

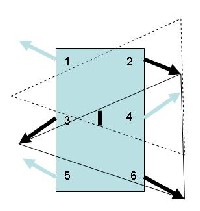
Unterstützt wird das ganze Gerät immer an den Fußpunkten der Beine. Verbindet man diese jeweils drei Punkte, ergeben sich zwei Dreiecke, die in den beiden Zeichnungen strichliert angedeutet sind. Teilweise überlappen sie sich, das ist der Bereich, wo sich der Schwerpunkt des ganzen Fahrzeuges befinden darf.

Und man sieht, dass diese Fläche bemerkenswert klein ist.

Für 3:3 laufen benötigt jedes Bein 2 Stellungen einmal vorn (A) und einmal hinten (B). Zuerst befinden sich die Beine 2,3 u 6 in Stellung A und werden auf dem Boden gleichzeitig in Stellung B bewegt. Dadurch schiebt sich der Roboter um das Stück A zu B nach vorn. Die Beine 1, 4 u 5 bewegen sich in der selben Zeit von Stellung B nach A, jedoch ohne Bodenkontakt. Wird nun diese Sequenz, im wechsel mit 1, 4 u 5 am Boden und 2, 3 u 6 in der Luft, zyklisch ausgeführt, hat man schon ein passables Laufprogramm für gerade aus.

geradeaus 2:4

Bei dieser Variante wird jeweils ein Beinpaar gleichzeitig bewegt. Diese sind günstigerweise: 1 und 4 (Paar 1); 3 und 6 (Paar 2); 2 und 5 (Paar 3) Jedes Beinpaar benötigt jedoch 3 Stellungen: A, B, C. Der Algoritmus teilt sich daher auch in drei Schritte auf I, II und III.

Für Schritt I bringen wir Paar 1 in Stellung A, Paar 2 in Stellung C und Paar 3 in Stellung B. Für Schritt II bewegt sich Paar 1 in Stellung B, Paar 2 in Stellung A (diese Bewegung muss ohne Bodenkontakt erfolgen) und Paar 3 in Stellung C. Für Schritt III bewegt sich Paar 1 in Stellung C, Paar 2 in Stellung B und Paar 3 in Stellung A (auch wieder in der Luft) Ab hier wiederholt sich das Programm

Fazit: Die Bewegungn sind etwas aufwendiger sich zu überlegen und zu programmieren, der Roboter gewinnt aber insgesammt an Stabilität und ist nur etwas langsamer als bei 3:3.

geradeaus 1:5

Diese Variante ist die langsamste, aber dafür am stabilsten, denn das Gewicht verteilt sich auf 5 Standbeine. Es werden 6 Stellungen pro Bein benötigt (A, B, C, D, E, F) und 6 Schritte. Es gibt mehrere Möglichkeiten der Startaufstellung ich will hier eine kurz Darstellen: Bein 1: A -> B -> C usw.
Bein 2: D -> E -> F
Bein 3: E -> F --> A
Bein 4: B -> C -> D
Bein 5: C -> D -> E
Bein 6: F --> A -> B

Die Pfeile geben an in Welche Stellung sich die Beine als nächstes bewegen, Bein 6 wird sich in die Stellung A bewegen. Dieser Rückstellvorgang muss immer in der Luft erfolgen. So wird sich der Roboter kontinuierlich vorwärts bewegen.

Hexapods in der Kurve

Nochmals das Bild von oben

Die effektiven Beinwege s können auch wie die Räder von einem sechsrädrigen Fahrzeug verstanden werden.

Wenn wir nun eine Kurve beschreiben wollen, verkürzen wir die Wege s auf einer Seite, dadurch ergibt sich ein Drehpunkt P

Was man sieht: Es muss eigentlich jedes Bein eine individuelle Bewegung machen. UND: jedes Bein muss seinen eigenen Kurvenradius einhalten

Hexapods drehen

Alternativ, etwas einfacher zu programmieren, weil die Stellungen von Oben weiter verwendet werden können ist das Panzer Modell. Konkret heisst es, die rechte Seite der Beine bewegt sich weiter nach oben, wärend die linke Seite der Beine sich nach unten bewegt. Dadurch wird der Roboter auf der Stelle gedreht. D.h. die Bewegungsrichtung der Beine ist insgesammt links zu rechts gegenläufig.

Kräfte am Spinnenbein

Da eine genaue Berechnung recht aufwendig ist und von vielen Faktoren zusätzlich stark beeinflusst wird (Dynamik und äußere Einflüsse), soll hier nur eine qualifizierende Betrachtung erfolgen.

Für Beine gibt es zwei völlig unterschiedliche Situationen:

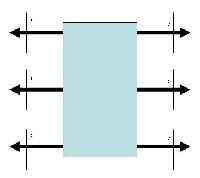
Ohne Bodenhaftung

(Glatteis)

Die Beine werden auseinandergedrückt. Das Kniegelenk muß versuchen, Ober- und Unterschenkel beisammenzuhalten, und in der Schulter muss das anteilige Gewicht des Fahrzeuges getragen werden. Durch die langen Hebel wird da, je nach Beinstellung, eine beachtliche Kraft erforderlich.

Mit Bodenhaftung

(Teppich)

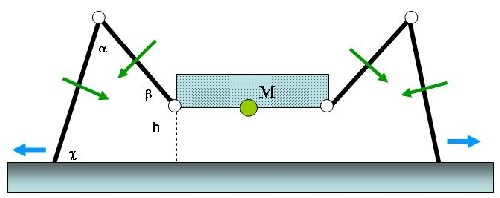
Ganz anders bei ausreichender Haftung: Da die Füße ja nicht wegrutschen, zieht das Gewicht des Fahrzeuges über die Oberschenkel die Knie nach innen. Hier müssen die Oberschenkel nach außen stemmen, um dem entgegenzuwirken.

Bitte beachten, die Beine können auch günstiger als auf dem Bild dargestellt, eingerichtet werden. Wenn der Oberschenkel waagrecht zum Roboterkörper ist. Muss das Schultergelenk zwar das gesammte Gewicht des Roboters tragen, aber das Kniegelenk wird praktisch vollständig entlastet. Auch bei Eis als Untergrund würde ein Wegrutschen der Beine so verhindert werden.

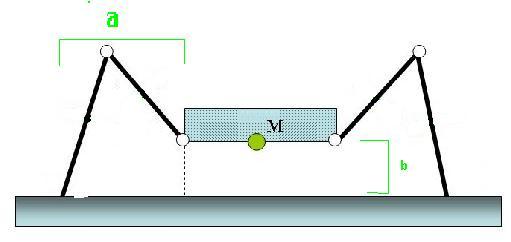
Ein Rechenbeispiel

Des weiteren ist es wichtig zu erwähnen, dass je nach Bauart des Beines, also welche die sich weiter an der Seite vom Bot befinden, enorme Hebelkräfte auftreten. Um die passenden Servos für seinen Roboter heraus zu suchen hier ein Rechenbeispiel:

Gegeben sei "a" als größtmöglicher Abstand zum Körper (blau). Je nach Bauart des Roboters und der Wahl der Bewegung sind entweder 3 oder 4 oder gar 5 Beine gleichzeit am Boden. Auf diese wird das gesammte Gewicht des Roboter verteilt. Uns interessiert an dieser Stelle wieviel Ncm im Schultergelenk notwendig sind um den Roboter hochzudrücken. Aus der Zeichnung wird wieder deutlich warum es sinnvoll ist den Unterschenkel möglichst senkrecht zu halten und den Oberschenkel waagrecht. Unter dieser Positionierung muss das Kniegelenk nämlich kein Drehmoment übertragen.

Aber zurück zur Rechnung.

das Drehmoment in der Schulter wird wie folgt berechnet: (Gewicht /Anzahl der Beine)* Hebelarm = Drehmoment in der Schulter

in unserem Beispielt a=10cm; G=1kg--> 1kg * 9,81m/s² = 9,81N ~ 10N; 3Beine am Boden

(10N / 3)* 10cm = 33,3Ncm

Wir benötigen also in der Schulter Servos welche mindestens 33,3Ncm schaffen, zur Sicherheit wären 35Ncm sinnvoller. Die Rechnung lässt sich natürlich auch so umstellen, dass anhand der Servos das Gesamtgewicht ermittelt werden kann:

(Drehmoment der Servos / Hebelarm)* Anzahl der Beine = Gewicht des Roboters

Dasselbe gilt natürlich auch für Quadropods. Nur muss man die Faktoren der Anzahl der Beine ändern

Siehe auch

Servos

Lynxmotion, Referenz für Roboter mit Beinen