Getriebe: Unterschied zwischen den Versionen

Version vom 25. Juni 2007, 20:58 Uhr (Quelltext anzeigen) User529 (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 25. Juni 2007, 20:58 Uhr (Quelltext anzeigen) User529 (Diskussion | Beiträge) Zum nächsten Versionsunterschied →
Zeile 2:		Zeile 2:
	== Mathematische Grundlagen ==		== Mathematische Grundlagen ==
	=== Übersetzungsfaktor ===		=== Übersetzungsfaktor ===
−	Der Übersetzungsfaktor <math>n</math> beschreibt das Zähnezahlenverhältnis, Durchmesser oder Drehmomentenverhältnis und das Drehzahlenverhältnis <math>s^{-1}</math>. Um Unklarheiten vorzubeugen haben sich aber die Begriffe Untersetzung für Drehzahlenänderungen ins langsame (antreibendes Rad dreht schneller) und Übersetzung für Drehzahlenänderungen ins schnelle (antreibendes Rad dreht langsamer) durchgesetzt.	+	Der Übersetzungsfaktor <math>n</math> beschreibt das Zähnezahlenverhältnis, Durchmesser oder Drehmomentenverhältnis und das Drehzahlenverhältni <math>s^{-1}</math>. Um Unklarheiten vorzubeugen haben sich aber die Begriffe Untersetzung für Drehzahlenänderungen ins langsame (antreibendes Rad dreht schneller) und Übersetzung für Drehzahlenänderungen ins schnelle (antreibendes Rad dreht langsamer) durchgesetzt.
	===Drehzahl===		===Drehzahl===

---

Version vom 25. Juni 2007, 20:58 Uhr

Dieser Artikel ist noch lange nicht vollständig. Der Auto/Initiator hofft das sich weitere User am Ausbau des Artikels beteiligen. Das Ergänzen ist also ausdrücklich gewünscht! Besonders folgende Dinge würden noch fehlen: Was ist die Modulgrösse und wie ermittelt man sie?

Mathematische Grundlagen

Übersetzungsfaktor

Der Übersetzungsfaktor

$$n$$ beschreibt das Zähnezahlenverhältnis, Durchmesser oder Drehmomentenverhältnis und das Drehzahlenverhältni $$s^{-1}$$ . Um Unklarheiten vorzubeugen haben sich aber die Begriffe Untersetzung für Drehzahlenänderungen ins langsame (antreibendes Rad dreht schneller) und Übersetzung für Drehzahlenänderungen ins schnelle (antreibendes Rad dreht langsamer) durchgesetzt.

Drehzahl

Da bei Zahnradgetrieben die Umfangsgeschwindigkeiten

$$U$$ beider ineinander greifenden Zahnräder gleich groß sein müssen, lässt sich die Übersetzung durch Gleichsetzen der Gleichungen für die Umfangsgeschwindigkeiten errechnen:

$$U_\mathrm{1}=w_\mathrm{1} \cdot r_\mathrm{1}$$

$$r_\mathrm{1}=z_\mathrm{1} \cdot m$$

$$U_\mathrm{2}=w\cdot r_\mathrm{2}$$

$$r_\mathrm{2}=z_\mathrm{2}\cdot m$$

Einsetzen in die Gleichung:

$$U_\mathrm{1}=U_\mathrm{2}$$

$$w_\mathrm{1} \cdot m \cdot z_\mathrm{1}=w_\mathrm{2} \cdot m \cdot z_\mathrm{2}$$

der Modul

$$m$$ muss bei beiden Zahnrädern gleich groß sein und kann daher gekürzt werden

$$\frac{w_\mathrm{1}}{w_\mathrm{2}}=\frac{z_\mathrm{2}}{z_\mathrm{1}}$$

Statt der Winkelgeschwindigkeit

$$w$$ können wir auch die Drehzahl $$n$$ einsetzen, da zwischen $$w$$ und $$n$$ nur der konstante Faktor $$2pi$$ steht, der ebenfalls gekürzt wird.

$$\frac{n_\mathrm{1}}{n_\mathrm{2}}=\frac{z_\mathrm{2}}{z_\mathrm{1}}$$

Drehmomente

Die über ein Getriebe übertragene Leistung

$$P$$ ist in erster Näherung konstant (bis auf den Wirkungsgrad), deshalb kann $$P=M \cdot w$$ auf die Leistung gleichgesetzt werden. (eine andere Möglichkeit zur Herleitung geht über das Hebelgesetz, und über den Ansatz dass beide Umfangskräfte gleich groß sein müssen)

$$P_\mathrm{ein}=P_\mathrm{aus}$$

$$M_\mathrm{ein} \cdot w_\mathrm{ein}=M_\mathrm{aus} \cdot w_\mathrm{aus}$$

Komplexere Getriebe

Einfache Getriebe lassen sich mit den bis jetzt beschriebenen Formeln gut handhaben, bei Umlaufgetrieben stoßen diese aber sehr schnell an ihre Grenzen. Der so genannte Kurzbachplan hilft hierbei:

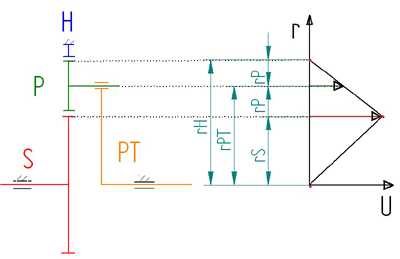
Jedes Planetengetriebe lässt sich in Sonnenrad (S rot) Planetenrad (P grün) Planetenträger (PT orange) und Hohlrad (H blau) zerlegen. Neben das maßstäblich gezeichnete Getriebe werden nun in ein Koordinatensystem bekannte Umfangsgeschwindigkeiten vorgegebener Punkte eingetragen (rote Punkte), diese sind entweder Null (am stehenden Hohlrad und im Zentrum der Antriebswelle)) oder aus Radius und Drehzahl berechenbar (Sonnenrad). Jetzt werden diese Punkte miteinander verbunden, und aus den Schnittpunkten dieser Linie der Achse des Planetenrades (=Radius des Planetenträgers) lässt sich nun die Drehzahl des Planetenträgers berechnen (=Abtrieb). Gezeichnete Beziehungen lassen sich auch mathematisch mit dem Strahlensatz und der zuvor kennen gelernten Gleichung für

$$U$$ ausdrücken und auf ein $$n_\mathrm{ges}$$ zusammenfassen.

Möge sich jemand meiner Schlechtschreibfehler annehmen; werde morgen (und wenn nit dann, dann irgendwann) weiter schreiben, mfg Clemens

Getriebe selbst entwerfen

Achsabstände

Das größte Problem bei selbstgebauten Getrieben ist die Bestimmung der Achsabstände. Zu weite Abstände verursachen zum Einen Schäden an den Zähnen und zu kurze Abstände sorgen dafür, dass sich das Getriebe, wenn überhaupt, nur schwer drehen lässt und auch schneller verschleissen kann.

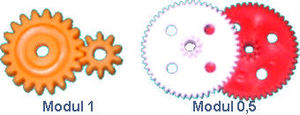
Ein wichtiger Parameter, welcher zur Berechnung der Achsabstände benötigt wird, ist die Modulgröße, auch Modulzahl genannt.

Für Zahnräder mit unbekannter Modulgröße gibt es Zahnradlehren, welche das Ermitteln des Moduls erleichtern, ohne raten zu müssen

Der Abstand der Zahnradachsen lässt sich wie folgt ermitteln:

  Anzahl der beiden Zahnradzähne zusammenzählen,
  davon dann die Hälfte mit der Modulzahl multiplizieren.
  
  (Z1 + Z2) / 2 * Modulzahl = Achsabstand

  Beispiel: 
     Zahnrad1 = 50 Zähne, Zahnrad2 = 10 Zähne jeweils Modul 0,5
     50 + 10 = 60 / 2 = 30 * 0,5 = 15
     Achsabstand = 15mm

Getriebebox

Mein erstes selbstgebautes Getriebe, die TwinMotor-Gearbox

Die Wellen (Achsen) sind natürlich nicht mit beiden Hälften verbunden. Ein Messingrohr (D=3mm/2mm), in welches ein Messingstab (d=2mm) eingelötet wurde und als "Zapfwelle" zusammengesteckt, sollten viel Platz sparen.

Leider ist der Reibungswiderstand etwas hoch geworden, sodass die Motoren nur unrund laufen und mit steigender Betriebsdauer (Temperatur) immer mehr Kraft benötigen (der gut schmiert...).

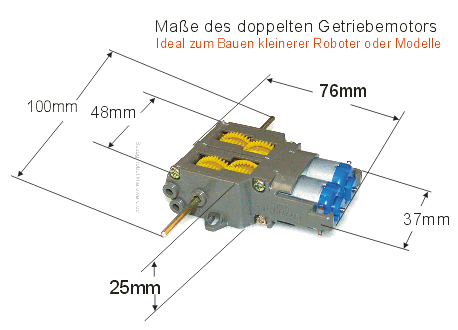
Aber für den ersten Aufbau dieser Art dennoch ein gutes Ergebnis. Für Bastler mit weniger Kentnissen gibt es inzwischen auch Bausätze für ganz ähnliche Getriebemotoren. Beispielsweise der TwinMotor:

Die nächste Eigenversion wird dann doch noch richtig gelagert werden müssen, Sinter- oder Kugel-/Rollen-Lager steht noch nicht fest.

Autor

• Darwin.nuernberg 17:55, 5. Mär 2006 (CET)
• user52920:51, 25. Juni

Siehe auch

• Getriebemotoren
• Zahnrad